Sudden Area Change (TL)
Sudden expansion or contraction in flow area
Libraries:
Simscape /
Fluids /
Thermal Liquid /
Pipes & Fittings
Description
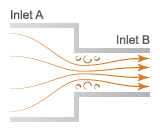
The Sudden Area Change (TL) block models the minor pressure losses due to a sudden change in flow cross-sectional area. The area change is a contraction from port A to port B and an expansion from port B to port A. This component is adiabatic. It does not exchange heat with its surroundings.
Sudden Area Change Schematic

Mass Balance
The mass conservation equation in the sudden area change is
where:
and are the mass flow rates into the sudden area change through ports A and B.
Momentum Balance
The momentum conservation equation in the sudden area change is
where:
pA and pB are the pressures at ports A and B.
is the average mass flow rate.
ρ is the average fluid density.
SA and SB are the flow cross-sectional areas at ports A and B.
ΦLoss is the mechanical energy loss due to the sudden area change.
The mechanical energy loss is
where:
KLoss is the loss coefficient.
If the Loss coefficient specification parameter is set to
Semi-empirical formulation, the loss coefficient for
a sudden expansion is computed as
while for a sudden contraction it is computed as
where:
Ke is the correction factor in the expansion zone.
Kc is the correction factor in the contraction zone.
In the transition zone between sudden expansion and sudden contraction behavior, the block smooths the loss coefficient
where
where ṁCr is the threshold mass flow rate for flow reversal,
If the Loss coefficient specification parameter is set to
Tabulated data — Loss coefficient vs. Reynolds
number, the block obtains the loss coefficient from tabular data
provided as a function of the Reynolds number.
Energy Balance
The energy conservation equation in the sudden area change is
where:
ΦA and ΦB are the energy flow rates into the sudden area change through ports A and B.
Assumptions and Limitations
The flow is incompressible. The fluid density is assumed constant in the sudden area change.
Ports
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2016a