Estimate Regularized ARX Model Using System Identification App
This example shows how to estimate regularized ARX models using automatically generated regularization constants in the System Identification app.
Open Saved App Session
Open the saved app session file.
systemIdentification("ex_arxregul.sid")
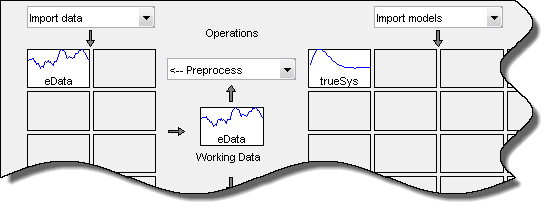
The session imports the following data and model into the System Identification app:
Transfer function model
trueSys.Estimation data
eData. The data is collected by simulating thetrueSyssystem.
The trueSys transfer function is:
Estimate 50th-Order ARX Model
In the System Identification app, select Estimate > Polynomial Models to open the Polynomial Models dialog box.
Verify that ARX is selected in the Structure list.
In the Orders field, specify [0 50 0] as the ARX model order and delay.
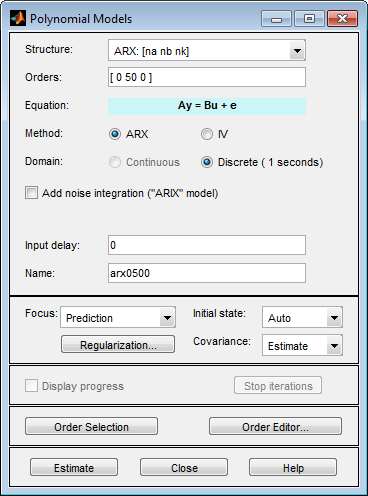
Click Estimate to estimate the model.
A model arx0500 is added to the System Identification app.
Estimate 50th-Order Regularized ARX Model
In the Polynomial Models dialog box, click Regularization.
In the Regularization Options dialog box, select
TCfrom the Regularization Kernel drop-down list.
Specifying this option automatically determines regularization constants using the
TCregularization kernel. To learn more, see thearxRegulreference page.Click Close to close the dialog box.
In the Name field in the Polynomial Models dialog box, type
arx0500reg.Click Estimate.
A model arx0500reg is added to the System Identification app.

Compare Model Outputs to Estimation Data
Select the Model output check box in the System Identification app.
The Measured and simulated model output plot shows that both the models have an 84% fit with the data.

Check Parameter Value Variance for Regularized Model
Because the model fit to the estimation data is similar with and without using
regularization, compare the impulse response of the ARX models with the impulse responses of
trueSys, the system used to collect the estimation data.
Click the
trueSysicon in the model board of the System Identification app.
Select the Transient resp check box to open the Transient Response plot window.

By default, the plot shows the step response.
In the Transient response plot window, select Options > Impulse response to change to plot to display the impulse response.
Select Options > Show 99% confidence intervals to plot the confidence intervals.

The plot shows that the impulse response of the unregularized model
arx0500is far off from the true system and has large uncertainties.
To get a closer look at the model fits to the data and the variances, magnify a portion of the plot.

The fit of the regularized ARX model
arx0500regclosely matches the impulse response of the true system and the variance is greatly reduced as compared to the unregularized model.