Plan Path for a Differential Drive Robot in Simulink
This example demonstrates how to execute an obstacle-free path between two locations on a given map in Simulink®. The path is generated using a probabilistic road map (PRM) planning algorithm (mobileRobotPRM). Control commands for navigating this path are generated using the Pure Pursuit controller block. A differential drive kinematic motion model simulates the robot motion based on those commands.
Load the Map and Simulink Model
Load the occupancy map, which defines the map limits and obstacles within the map. exampleMaps.mat contains multiple maps including simpleMap, which this example uses.
load exampleMaps.matSpecify a start and end location within the map.
startLoc = [5 5]; goalLoc = [20 20];
Model Overview
Open the Simulink model.
open_system('pathPlanningSimulinkModel.slx')The model is composed of three primary parts:
Planning
Control
Plant Model
Planning
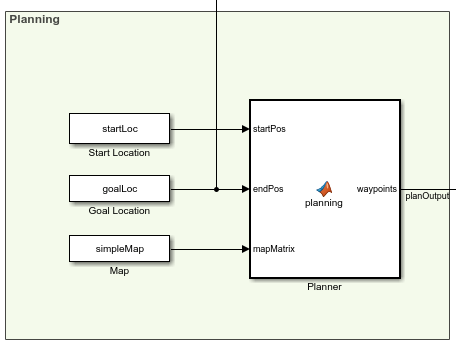
The Planner MATLAB® function block uses the mobileRobotPRM path planner and takes a start location, goal location, and map as inputs. The blocks outputs an array of waypoints. The robot follows these waypoints to reach the goal position. The planned waypoints are used downstream by the Pure Pursuit controller block.
Control
Pure Pursuit

The Pure Pursuit controller block generates the linear velocity and angular velocity commands based on the waypoints and the current pose of the robot.
Check if Goal is Reached

The Check Distance to Goal subsystem calculates the current distance to the goal and if it is within a threshold, the simulation stops.
Plant Model

The Differential Drive Kinematic Model block creates a vehicle model to simulate simplified vehicle kinematics. The block takes linear and angular velocities as command inputs from the Pure Pursuit controller block, and outputs the current position and velocity states.
Run the Model
simulation = sim('pathPlanningSimulinkModel.slx');Visualize The Motion of Robot
After simulating the model, visualize the robot driving the obstacle-free path in the map.
map = binaryOccupancyMap(simpleMap); robotPose = simulation.Pose; thetaIdx = 3; % Translation xyz = robotPose; xyz(:, thetaIdx) = 0; % Rotation in XYZ euler angles theta = robotPose(:,thetaIdx); thetaEuler = zeros(size(robotPose, 1), 3 * size(theta, 2)); thetaEuler(:, end) = theta; % Plot the robot poses at every 10th step. for k = 1:10:size(xyz, 1) show(map) hold on; % Plot the start location. plotTransforms([startLoc, 0], eul2quat([0, 0, 0])) text(startLoc(1), startLoc(2), 2, 'Start'); % Plot the goal location. plotTransforms([goalLoc, 0], eul2quat([0, 0, 0])) text(goalLoc(1), goalLoc(2), 2, 'Goal'); % Plot the xy-locations. plot(robotPose(:, 1), robotPose(:, 2), '-b') % Plot the robot pose as it traverses the path. quat = eul2quat(thetaEuler(k, :), 'xyz'); plotTransforms(xyz(k,:), quat, 'MeshFilePath',... 'groundvehicle.stl'); light; drawnow; hold off; end
![Figure contains an axes object. The axes object with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 16 objects of type patch, line, image, text.](../../examples/robotics/win64/PlanPathForADifferentialRobotInSimulinkExample_05.png)
© Copyright 2019 The MathWorks, Inc.