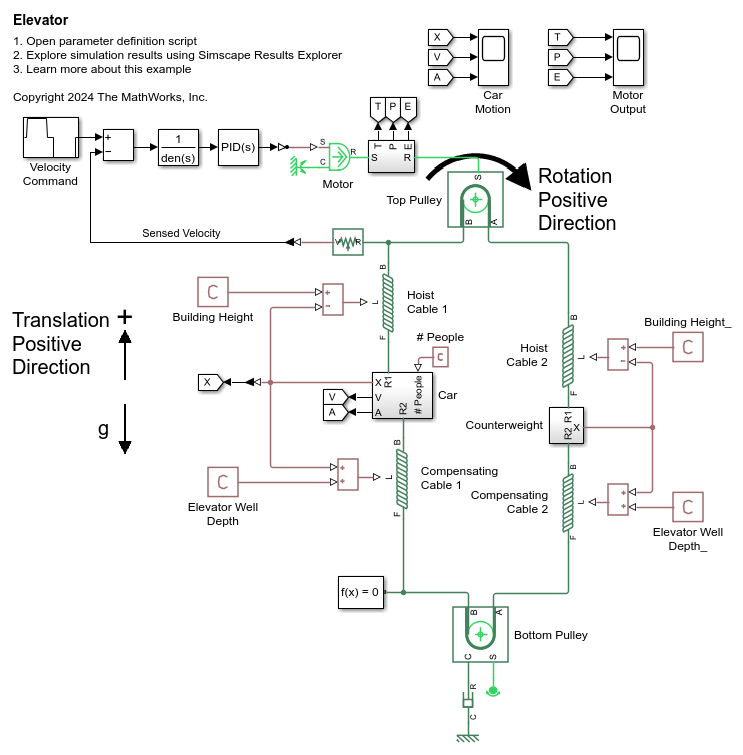
Cable
Libraries:
Simscape /
Driveline /
Couplings & Drives
Description
The Cable block represents an element that transfers tension between two contact points. You can treat the block as an arbitrary tension transfer device to simulate a variety of situations, including pulley networks, cable drives, and serpentine belts. You can choose whether the cable exhibits slack upon loss of tension. The block has a base port, B, and a follower port, F. The cable stretches in tension when the base port leads the follower port.
The block considers only the longitudinal translational motion and force exerted at the cable ends. The first figure shows a Translational Spring and Translational Damper block in parallel, which is functionally equivalent to the Cable block with zero mass. The second figure shows the same spring and damper blocks but with an additional Mass block on either side, which is functionally equivalent to the Cable block with a nonzero mass.
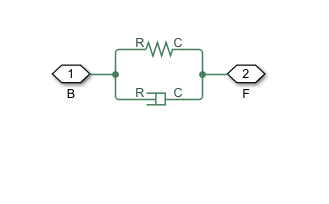
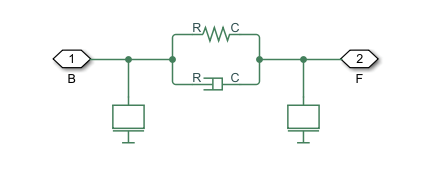
These figures only apply when the cable is in tension.
Tip
Confirm that your model operates as expected before you select the Model slack and Model mass parameters. Verify that the B and F ports are oriented properly by viewing the tension plots of each cable in the Simscape Results Viewer and looking for unexpected negative values.
The Cable block can act as a rope, belt, cable, or any other device that has tensile strength and transmits tension between two contact points. A contact point can be a pulley, a drum, or an ideal source. You can use the Stretch parameterization parameter to control whether the block acts as a constant or tabulated connection.
You can use this block to model stationary or travelling pulley networks. You can drive the Cable block with sources like the Ideal Translational Velocity Source block, or a Rope Drum block attached to an Ideal Force Source block.
For greater fidelity or numerical stability, you can choose to model the effect of mass on the system. When you select Model mass, the block distributes half of the total mass to either end of the cable. Adding a small amount of mass can improve the initialization of your model. You can also specify the initial conditions of the cable. If you choose to simulate slack, the block does not apply stiffness and damping when the cable is in slack. Selecting Model slack or Model mass enables the Model gravity parameter. Including the effect of gravity improves accuracy for heavy cable segments.
For cable segments with variable rest length, use the Model variable rest length parameter to improve results for travelling pulley applications. The block supports these examples of variable rest length scenarios:
One end of the cable is stationary, and the other end connects to a travelling pulley.
A cable is connected to a travelling pulley at each end.
You must use the correct orientation for the block when you select Model variable rest length. To learn more, see Best Practices for Modeling Pulley Networks.
Equations
The block equations refer to these quantities:
F is the tension force, where
xs is the deformation due to stretching, which you specify by using the Stretch variable. Simscape Results Explorer displays this quantity as
s.K is the spring stiffness coefficient. when you select Model slack and .
D is the damping coefficient.
m is the total mass, which you specify by using the Mass parameter. The block distributes half of the total mass to each end.
xB is the position of the base node.
xF is the position of the follower node.
ẋs is the stretch velocity.
LRest is the rest length of the cable segment.
Lmin is the Minimum rest length parameter.
μ is the Linear density parameter.
The Cable block responds to external load at the port B as
and port F as,
where . The definitions of D and V depend on the parameterization.
D and K are constant when you set Stretch parameterization to
Constant stiffness and dampingand clear Model variable rest length.D is constant and K = EA/LRest when you set Stretch parameterization to
Constant stiffness and dampingand select Model variable rest length, where EA is the value of the Rigidity parameter.D = TLU(xs) and K = TLU(xs) when you set Stretch parameterization to
Tabulated stiffness and dampingand clear Model variable rest length.D = TLU(xs, xs/LRest) and K = TLU(LRest, xs/LRest) when you set Stretch parameterization to
Tabulated stiffness and dampingand select Model variable rest length.
The block overrides the value of K to
0 when you select Model slack and
xs < 0.
The forces vary as functions of time and the stretch deformation, xs. K and B are functions of xs, such that when there is no slack or you are not simulating slack. Otherwise, when slack occurs at . The same logic applies for B. The terms that involve mass only apply when you select the Model mass parameter.
When you select Model variable rest length, takes the length as an input at port L. To input the rest length, use a Translational Motion Sensor block to determine the motion of the cable segment. The block saturates the rest length such that
When you select Model variable rest length and Model mass, the block uses the value of the Linear density parameter to determine the mass of the cable segment such that
When you select Model variable rest length, Model mass, and Model gravity, the block applies gravity to each end of the cable segment, such that
Positive cable velocity acts from port B to port
F. Positive gravity acts downward according to the cable orientation.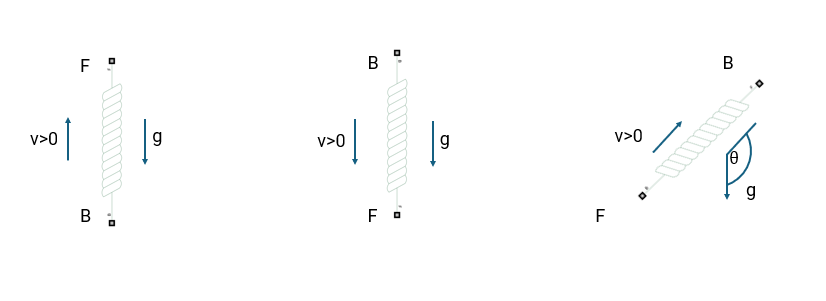
Variables
To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.
Limitations
When you select the Model mass and Model variable rest length parameters, the block uses a quasi-static model to calculate force due to mass. The block does not account for the rate of change in the cable segment mass. You can use a Variable Mass block to include the effect of the varying mass on the tension due to mass.