Comparing SSA and Explicit Tau-Leaping Stochastic Solvers
This example shows how to build and simulate a model using the SSA stochastic solver and the Explicit Tau-Leaping solver.
The following decaying-dimerizing reactions will be constructed and stochastically simulated:
Reaction 1: s1 -> null, with reaction rate constant, c1 = 1.0
Reaction 2: 2 s1 < - > s2, with reaction rate constants, forward: c2f = 0.002 reverse: c2r = 0.5
Reaction 3: s2 -> s3, with reaction rate constant, c3 = 0.04
Initial conditions: s1 = 100000 molecules, s2 = s3 = 0
This example uses parameters and conditions as described in Daniel T. Gillespie, 2001, "Approximate accelerated stochastic simulation of chemically reacting systems," Journal of Chemical Physics, vol. 115, no. 4, pp. 1716-1733.
Create Decaying-Dimerizing Model
model = sbiomodel('Decaying-Dimerizing Reaction Set');Enter Reactions
r1 = addreaction(model, 's1 -> null'); r2 = addreaction(model, '2 s1 <-> s2'); r3 = addreaction(model, 's2 -> s3');
Set Reactions to be MassAction
kl1 = addkineticlaw(r1, 'MassAction'); kl2 = addkineticlaw(r2, 'MassAction'); kl3 = addkineticlaw(r3, 'MassAction');
Add Rate Constants for Each Reaction
p1 = addparameter(kl1, 'c1', 'Value', 1.0); p2f = addparameter(kl2, 'c2f', 'Value', 0.002); p2r = addparameter(kl2, 'c2r', 'Value', 0.5); p3 = addparameter(kl3, 'c3', 'Value', 0.04);
Set the Kinetic Law Constants for Each Kinetic Law.
kl1.ParameterVariableNames = {'c1'};
kl2.ParameterVariableNames = {'c2f', 'c2r'};
kl3.ParameterVariableNames = {'c3'};Specify Initial Amounts of Each Species
model.species(1).InitialAmount = 100000; % s1 model.species(2).InitialAmount = 0; % s2 model.species(3).InitialAmount = 0; % s3
Display the Completed Model Objects
model
model =
SimBiology Model - Decaying-Dimerizing Reaction Set
Model Components:
Compartments: 1
Events: 0
Parameters: 4
Reactions: 3
Rules: 0
Species: 3
Observables: 0
Display the Reaction Objects
model.Reactions
ans = SimBiology Reaction Array Index: Reaction: 1 s1 -> null 2 2 s1 <-> s2 3 s2 -> s3
Display the Species Objects
model.Species
ans = SimBiology Species Array Index: Compartment: Name: Value: Units: 1 unnamed s1 100000 2 unnamed s2 0 3 unnamed s3 0
Get the Active Configuration Set for the Model.
cs = getconfigset(model,'active');Simulate Model Using SSA Stochastic Solver and Plot
tfinal = 30, logging every 10th datapoint.
cs.SolverType = 'ssa'; cs.StopTime = 30; solver = cs.SolverOptions; solver.LogDecimation = 10; cs.CompileOptions.DimensionalAnalysis = false; [t_ssa, x_ssa] = sbiosimulate(model); h1 = subplot(2,1,1); plot(h1, t_ssa, x_ssa(:,1),'.'); h2 = subplot(2,1,2); plot(h2, t_ssa, x_ssa(:,2:3),'.'); grid(h1,'on'); grid(h2,'on'); title(h1,'Decay Dimerizing Reactions'); ylabel(h1,'Amount of S1'); ylabel(h2,'Amount of S2 & S3'); xlabel(h2,'Time'); legend(h2, 'S2', 'S3');
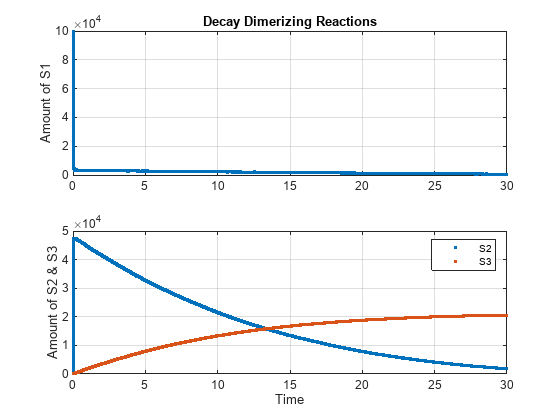
Simulate Model Using Explicit Tau-Leaping Solver and Plot in the Same Figure
Without closing the figure window, plot the results from using the Explicit Tau-Leaping Solver.
tfinal = 30, logging every 10th datapoint. Acceptable error tolerance for solver, 0.03.
cs.StopTime = 30; cs.SolverType = 'explTau'; solver = cs.SolverOptions; solver.LogDecimation = 10; [t_etl, x_etl] = sbiosimulate(model); hold(h1,'on'); hold(h2,'on'); plot(h1, t_etl, x_etl(:,1),'o'); plot(h2, t_etl, x_etl(:,2:3),'o'); legend(h2, 'S2 (SSA)', 'S3 (SSA)', 'S2 (Exp. Tau)', 'S3 (Exp. Tau)'); hold(h1,'off'); hold(h2,'off');

Comparison of Number of Steps for SSA and Explicit Tau-Leaping Algorithms
fprintf('Approximate Number of SSA steps: %d\n', (length(t_ssa) * 10));Approximate Number of SSA steps: 616010
fprintf('Approximate Number of Explicit Tau-Leaping steps: %d\n', ... (length(t_etl) * 10));
Approximate Number of Explicit Tau-Leaping steps: 620
