Synchronous Machine (Six-Phase)
Libraries:
Simscape /
Electrical /
Electromechanical /
Synchronous
Description
The Synchronous Machine (Six-Phase) block models a six-phase synchronous machine, also known as a dual-star machine.
A six-phase synchronous machine has two groups of stator windings: the ABC group and the XYZ group. These two groups have a 30 degree phase shift.
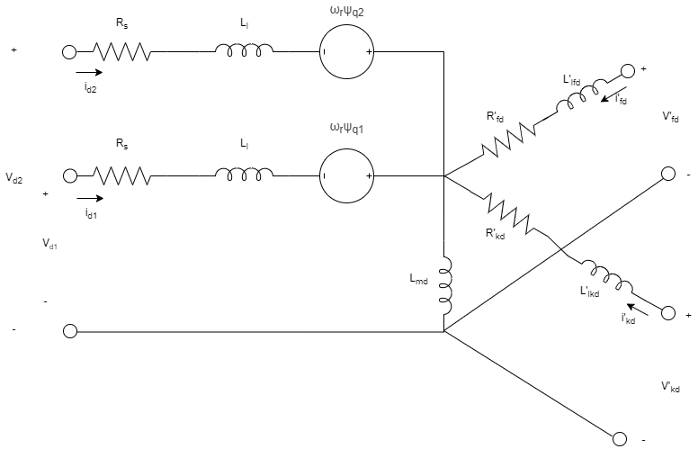
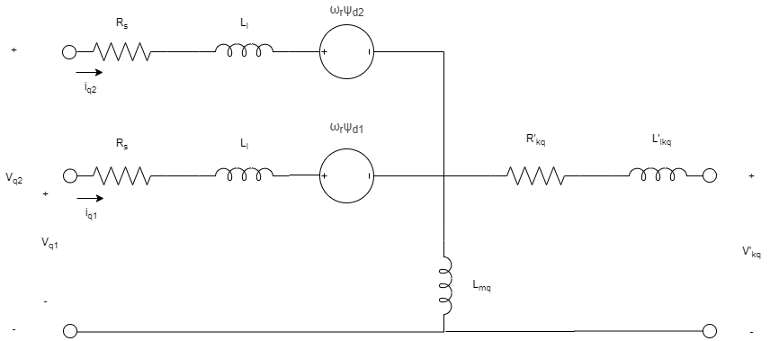
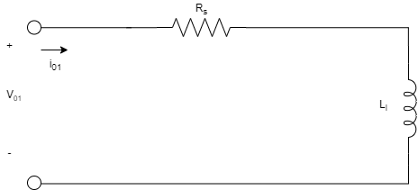
The equivalent circuits of the six-phase synchronous machine for the direct axis, the quadrature axis, and the two zero sequence are:
Equations
The synchronous machine equations are expressed with respect to a synchronously rotating reference frame, defined by:
where:
θe is the rotor electrical angle.
N is the number of pole pairs.
θr is the rotor mechanical angle.
x_rotor_offset is
0if you define the rotor electrical angle with respect to the d-axis, or-pi/2if you define the rotor electrical angle with respect to the q-axis.
Two Park transformations map the synchronous machine equations to the rotating reference frame with respect to the electrical angle. The Park transformation for the first group of stator windings, the ABC group, is defined by:
The Park transformation for the second group of stator windings, the XYZ group, is defined by:
The Park transformations are used to define the per-unit synchronous machine equations.
The stator voltage equations for the ABC group are defined by:
where:
vd1, vq1, and v01 are the d-axis, q-axis, and zero-sequence ABC stator voltages, defined by:
va, vb, and vc are the ABC stator voltages measured from port ~ABC to neutral port n1.
ωbase is the per-unit base electrical speed.
ψd1, ψq1, and ψ01 are the d-axis, q-axis, and zero-sequence stator flux linkages for the ABC group.
ωr is the per-unit rotor rotational speed.
Rs is the stator resistance.
id1, iq1, and i01 are the d-axis, q-axis, and zero-sequence ABC stator currents, defined by:
ia, ib, and ic are the ABC stator currents flowing from port ~ABC to port n1.
The stator voltage equations for the XYZ group are defined by:
where:
vd2, vq2, and v02 are the d-axis, q-axis, and zero-sequence XYZ stator voltages, defined by:
vx, vy, and vz are the XYZ stator voltages measured from port ~XYZ to neutral port n2.
ψd2, ψq2, and ψ02 are the d-axis, q-axis, and zero-sequence stator flux linkages for the XYZ group.
id2, iq2, and i02 are the d-axis, q-axis, and zero-sequence XYZ stator currents, defined by:
ix, iy, and iz are the XYZ stator currents flowing from port ~XYZ to port n2.
The rotor voltage equations are defined by:
where:
v'fd is the field winding voltage referred to the stator side.
v'kd and v'kq are the dq-axes damper winding voltages referred to the stator side. They are all equal to 0.
ψ'fd, ψ'kd, and ψ'kq are the magnetic fluxes linking the field circuit, the d-axis damper winding, and the q-axis damper winding.
R'fd, R'kd, and R'kq are the resistances of the rotor field circuit, d-axis damper winding, and q-axis damper winding.
i'fd, i'kd, and i'kq are the field and dq-axes damper winding currents referred to the stator side.
The stator flux linkage equations are defined by:
where:
Ll is the stator leakage inductance.
Lmd and Lmq are the mutual inductances of the stator d-axis and q-axis.
The rotor flux linkage equations are defined by:
where:
L'lfd is the rotor field winding inductance.
L'lkd is the rotor d-axis damper winding inductance.
L'lkg is the rotor q-axis damper winding inductance.
The rotor torque is defined by:
Model Thermal Effects
You can expose thermal ports to model the effects of losses that convert power to heat. To expose the thermal ports, set the Modeling option parameter to either:
No thermal port— The block contains expanded electrical conserving ports associated with the stator windings, but does not contain thermal ports.Show thermal port— The block contains expanded electrical conserving ports associated with the stator windings and thermal conserving ports for each of the windings and for the rotor.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Variables
To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
For this block, the Initial Targets settings are visible only if, in
the Initial Conditions section, you set the Initialization
option parameter to Set targets for rotor angle and Park's
transform variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
Ports
Conserving
Parameters
References
[1] Kieferndorf, F., Burzanowska , H., Kanerva S., Sario P. "Modeling of rotor based harmonics in dual-star, wound field, synchronous machines." 2008 18th International Conference on Electrical Machines: Vilamoura, 1-6.
[2] Burzanowska , H., Sario P, Stulz C., Joerg P. "Redundant Drive with Direct Torque Control (DTC) and dual-star synchronous machine, simulations and verifications." 2007 European Conference on Power Electronics and Applications: Aalborg, 1-10.
Extended Capabilities
Version History
Introduced in R2020b