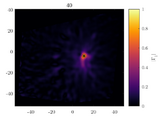
2D Vortex Core Tracking - Gamma 1 - Super Fast
Based on and inspired by Sebastian Endrikat https://www.mathworks.com/matlabcentral/fileexchange/52343-find-vortices-in-velocity-fields
Underlying math presented by L Graftieaux "Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows" https://iopscience.iop.org/article/10.1088/0957-0233/12/9/307/pdf
Thanks a lot!
Sebastian's code is rather slow, though, because it uses 4 nested for loops. Producing the gamma1 map can be done more efficiently in Matlab by realizing that the operations described in the Graftieaux's paper can be rearranged into two convolutions. This code does that, basically. It also find the maximum gamma 1 by fitting a spline curve, therefore not being limited by the grid resolution of the vector field.
The drawback is that it'll find only one vortex core, which might not be desired in some applications where multiple vortices form. One can, however, use the second output (G1) to perform their own peak finding/thresholding to find multiple vortex cores.
Write-up of the details on https://zigunov.com/2019/07/08/finding-vortex-cores-with-gamma-1/
Hope it was useful!
-FZ
Cita come
Fernando Zigunov (2024). 2D Vortex Core Tracking - Gamma 1 - Super Fast (https://www.mathworks.com/matlabcentral/fileexchange/72092-2d-vortex-core-tracking-gamma-1-super-fast), MATLAB Central File Exchange. Recuperato .
Compatibilità della release di MATLAB
Compatibilità della piattaforma
Windows macOS LinuxCategorie
- Sciences > Physics > Fluid Dynamics >
Tag
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Scopri Live Editor
Crea script con codice, output e testo formattato in un unico documento eseguibile.