Signal Processing Toolbox fornisce funzioni e app per gestire, analizzare, pre-elaborare ed estrarre feature da segnali campionati in modo uniforme o non uniforme. Il toolbox comprende gli strumenti per la progettazione e l'analisi di filtri, il ricampionamento, la linearizzazione, l’eliminazione del trend e la stima dello spettro di potenza. È possibile utilizzare l’app Signal Analyzer per visualizzare ed elaborare i segnali contemporaneamente nei domini di tempo, frequenza e tempo-frequenza. L’app Filter Designer consente di progettare e analizzare filtri digitali FIR e IIR. Entrambe le app generano script MATLAB per riprodurre o automatizzare il tuo lavoro.
Utilizzando le funzioni del toolbox è possibile preparare set di dati di segnali per l’addestramento del modello di intelligenza artificiale progettando feature in grado di ridurre la dimensionalità e migliorare la qualità dei segnali. È possibile consultare ed elaborare raccolte di file e set di dati di grandi dimensioni utilizzando i datastore di segnali. Con l’app Signal Labeler sarai in grado di annotare attributi, regioni e punti di interesse dei segnali per creare set di segnali etichettati. Il toolbox supporta l’accelerazione GPU oltre alla generazione di codice C/C++ e CUDA® per la prototipazione desktop e l’implementazione di sistemi embedded.
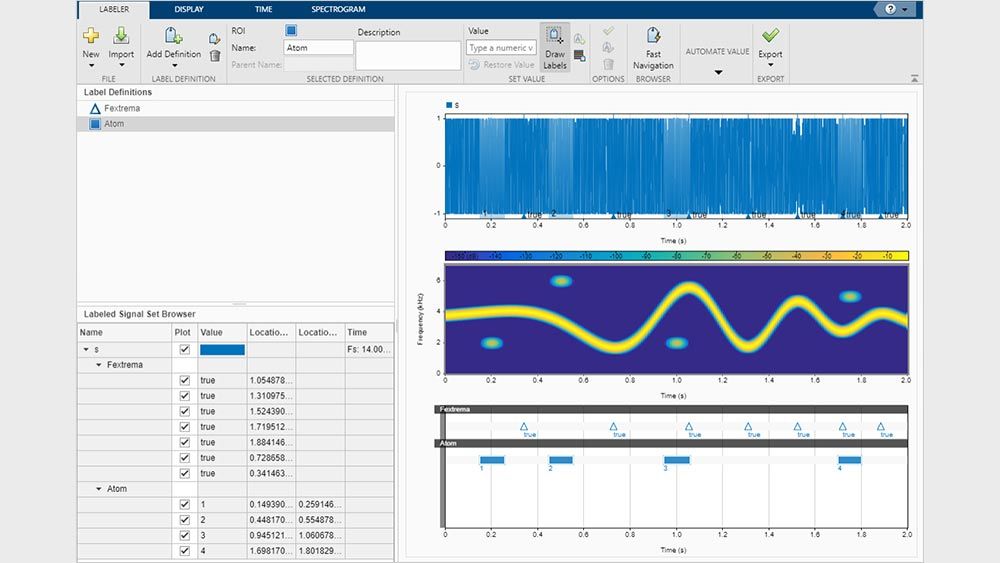
Machine Learning e Deep Learning per i segnali
Esegui operazioni di pre-elaborazione, progettazione di feature, etichettatura dei segnali e generazione di set di dati per workflow di Machine Learning e Deep Learning. Usa l’app Signal Labeler per creare set di dati di verità di base (ground truth) ed estrarre feature per addestrare modelli di intelligenza artificiale.
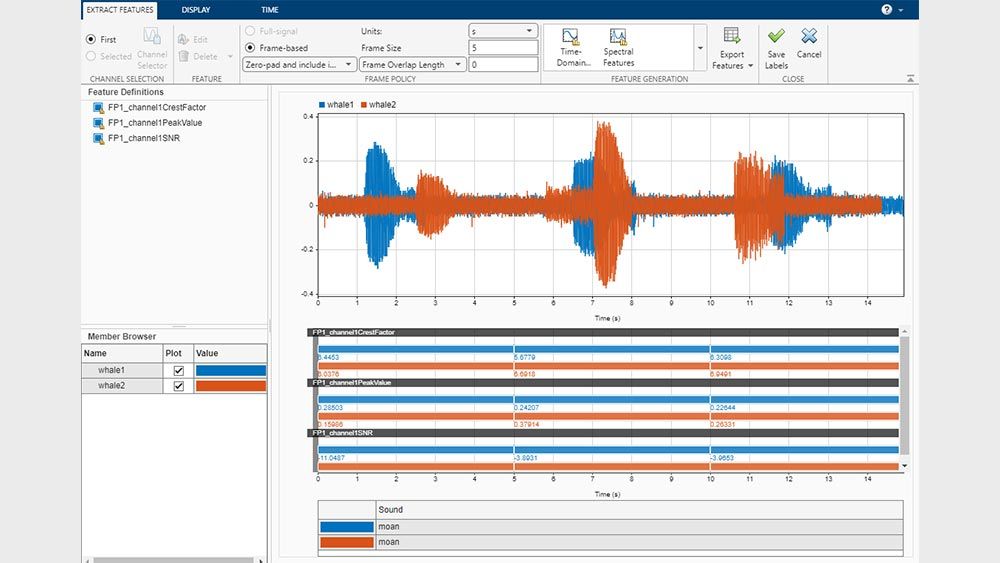
Estrazione di feature e misurazione di segnali
Misura ed estrai le feature distintive nei segnali inclusi picchi, potenza, larghezza di banda, distorsione e statistiche del segnale. Calcola le metriche relative a impulsi e transizioni. Estrai le feature per un intero set di dati con l’app Signal Labeler.
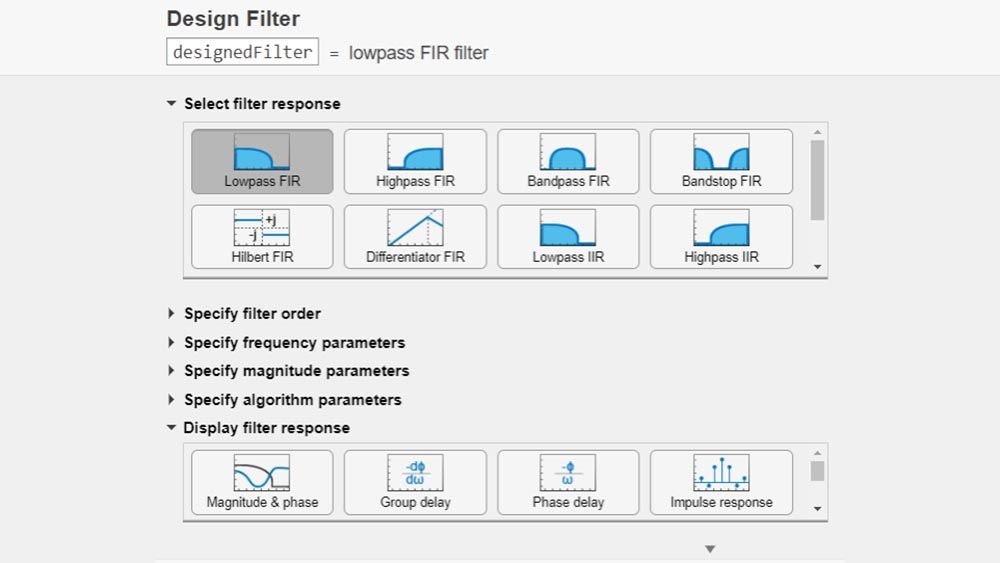
Progettazione e analisi di filtri
Progetta, analizza e implementa filtri digitali e analogici. Usa l’app Filter Designer o l’attività di Live Editor Progetta filtro per progettare una varietà di filtri digitali FIR e IIR, come passa-basso, passa-alto e stop banda.
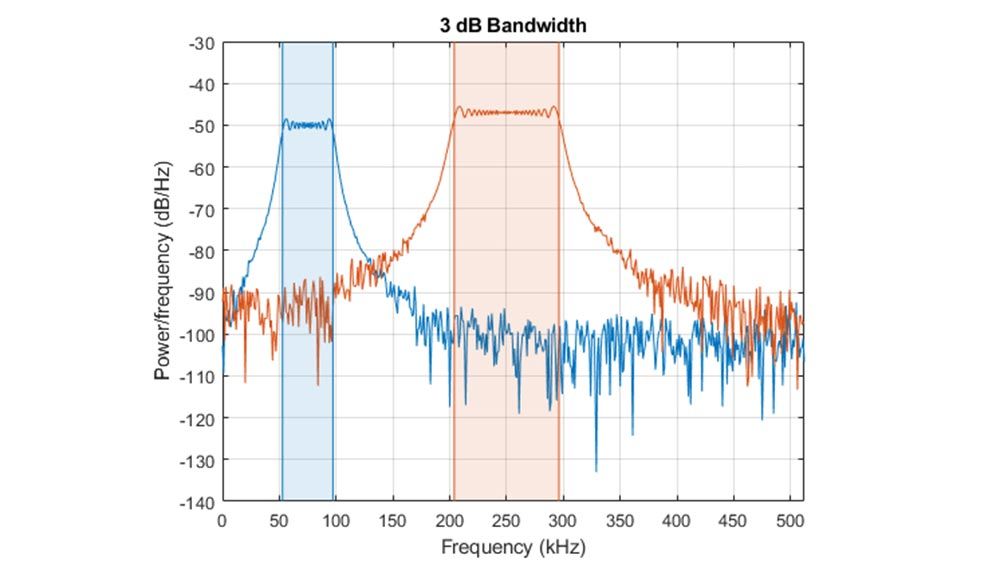
Analisi spettrale
Caratterizza il contenuto di frequenza di un segnale utilizzando la stima dello spettro e le tecniche del sottospazio. Progetta, visualizza e implementa funzioni di windowing.
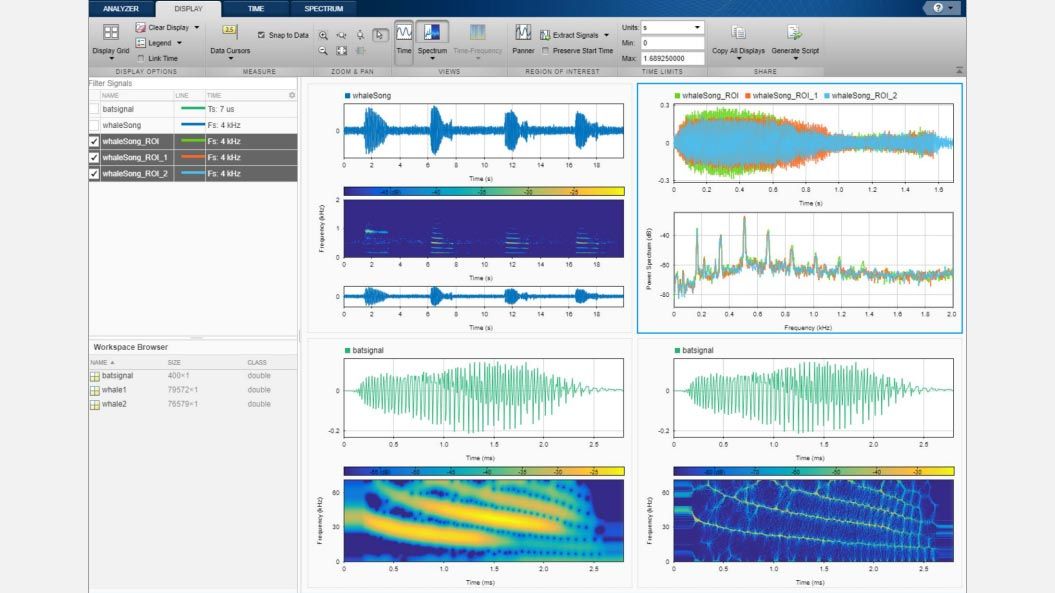
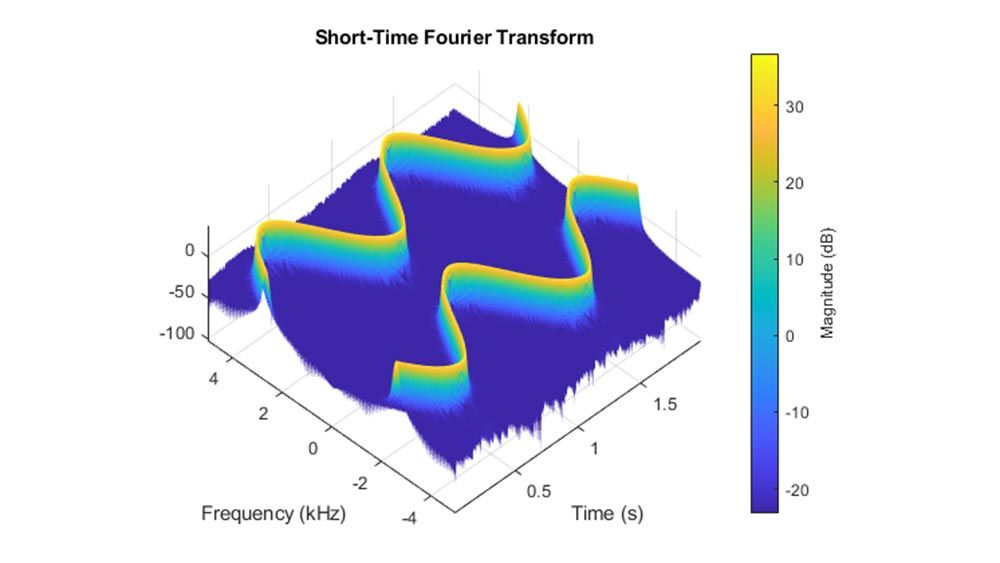
Analisi tempo-frequenza
Visualizza e confronta il contenuto di tempo-frequenza dei segnali non stazionari utilizzando metodi come lo spettrogramma, il synchrosqueezing e la riassegnazione.
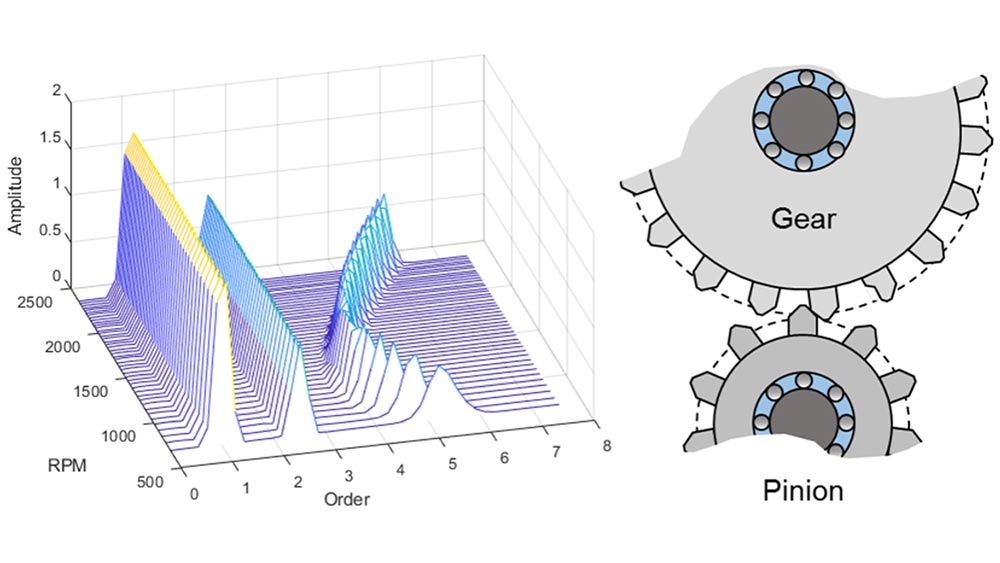
Analisi della vibrazione
Caratterizza le vibrazioni nei sistemi meccanici. Utilizza l’analisi degli ordini per analizzare e visualizzare il contenuto dello spettro presente nei macchinari rotanti. Esegui analisi modali sperimentali e analisi della fatica.
Accelerazione e generazione di codice
Accelera l’esecuzione degli algoritmi di elaborazione di segnali utilizzando un’unità di elaborazione grafica (GPU). Genera codice sorgente C/C++ portabile, eseguibili standalone o applicazioni standalone per il tuo codice MATLAB.
Risorse di prodotto:
Richiedi una versione di prova gratuita
30 giorni di prova a tua disposizione.
Pronto per acquistare?
Richiedi una quotazione e scopri i prodotti correlati.
Sei uno studente?
È possibile che la tua scuola già fornisca accesso a MATLAB, Simulink e ad altri prodotti complementari mediante una Campus-Wide License.