Subnormal Number Execution Speed
Subnormal numbers, formerly known as denormal numbers in floating-point
literature, fill the underflow gap around zero in floating-point arithmetic.
Subnormal values are a special category of floating-point values that are
too close to 0.0 to be represented as a normalized value.
The leading significand (mantissa) of a subnormal number is zero. When
adding and subtracting floating-point numbers, subnormal numbers prevent
underflow.
Using subnormal numbers provides precision beyond the normal representation by
using leading zeros in the significand to represent smaller values after the
representation reaches the minimum exponent. As the value approaches
0.0, you trade off precision for extended range.
Subnormal numbers are useful if your application requires extra
range.
However, in a real-time system, using subnormal numbers can dramatically increase execution latency, resulting in excessive design margins and real-time overruns. If the simulation or generated code performs calculations that produce or consume subnormal numbers, the execution of these calculations can be up to 50 times slower than similar calculations on normal numbers. The actual simulation or code execution time for subnormal number calculations depends on your computer operating environment. Typically, for desktop processors, the execution time for subnormal number calculations is five times slower than similar calculations on normal numbers.
To minimize the possibility of execution slowdowns or overruns due to subnormal number calculation latency, do one of the following:
In your model, manually flush to zero any incoming or computed subnormal values at inputs and key operations, such as washouts and filters. For an example, see Flush Subnormal Numbers to Zero.
To detect a subnormal value for a single precision, 32-bit floating-point number:
Find the smallest normalized number on a MATLAB® host. In the Command Window, type:
In the C language,>> SmallestNormalSingle = realmin('single')FLT_MIN, defined infloat.h, is equivalent torealmin('single').Look for values in range:
0 < fabsf(x) < SmallestNormalSingle
To detect a subnormal value for a double precision, 64-bit floating-point number:
Find the smallest normalized number on a MATLAB host. In the Command Window, type:
In the C language,>> SmallestNormalDouble = realmin('double')DBL_MIN, defined infloat.h, is equivalent torealmin('double').To detect a subnormal value, look for values in this range:
0 < fabs(x) < SmallestNormalDouble
Set the Simulation behavior for denormal numbers parameter to
Flush to zero (FTZ)to emulate flush-to-zero behavior for all denormal results from arithmetic operations. For more information, see Simulation behavior for denormal numbers.On your processor, set flush-to-zero mode or, with your compiler, specify an option to disable subnormal numbers. Flush-to-zero modes treat a subnormal number as 0 when it is an input to a floating-point operation. Underflow exceptions do not occur in flush-to-zero mode.
For example, in Intel® processors, the flush-to-zero (FTZ) and denormals-are-zero (DAZ) flags in the MXCSR register control floating-point calculations. For the gcc compiler on Linux,
-ffast-mathsets abrupt underflow (FTZ), flush-to-zero, while–O3 -ffast-mathreverts to gradual underflow, using subnormal numbers.
For more information, see the IEEE® Standard 754, IEEE Standard for Floating-Point Arithmetic.
Simulation Time with and Without Subnormal Numbers
This example shows how using subnormal numbers increases simulation time by ~5 times.
For this example, create a simple model
ex_subnormal that has a
Constant and a Gain block. The Gain is set to
subnormal value
realmin('double')/2.

To run a simulation, in the Command Window, type
for k=1:5, tic; sim('ex_subnormal');
toc,end. Observe the elapsed times for
simulation using subnormals, similar to the
following:
>> for k=1:5, tic; sim('ex_subnormal'); toc,end Elapsed time is 9.909326 seconds. Elapsed time is 9.617966 seconds. Elapsed time is 9.797183 seconds. Elapsed time is 9.702397 seconds. Elapsed time is 9.893946 seconds.
Set the Gain to a number, 2, that
is not a subnormal
value:
>> set_param('ex_subnormal/Gain', 'Gain', '2');
To run a simulation, in the Command Window, type
for k=1:5, tic; sim('ex_subnormal');
toc,end. Observe elapsed times for
simulations that do not use subnormal values,
similar to the following:
>> for k=1:5, tic; sim('ex_subnormal'); toc,end Elapsed time is 2.045123 seconds. Elapsed time is 1.796598 seconds. Elapsed time is 1.758458 seconds. Elapsed time is 1.721721 seconds. Elapsed time is 1.780569 seconds.
Flush Subnormal Numbers to Zero
This example shows how to flush single precision subnormal numbers to zero.
For this example, create a simple model
ex_flush_to_zero.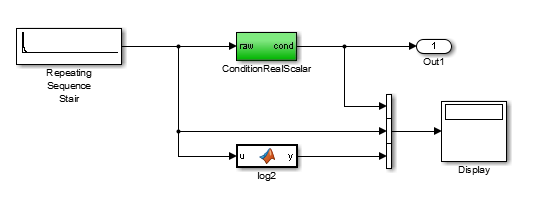
Repeating Sequence Stairgenerates a sequence of numbers from two raised to the power of 0 through two raised to the power of -165. The sequence approaches zero.ConditionRealScalarflushes subnormal single precision values that are less thanrealmin('single')to zero.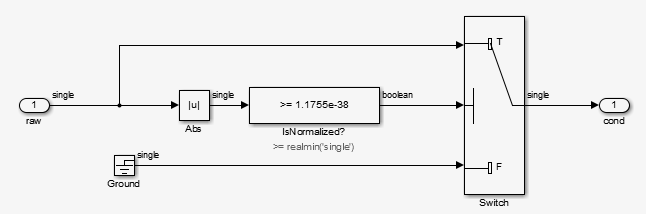
MATLAB function block
log2generates the base 2 logarithm of theRepeating Sequence Stairoutput. Specifically,log2generates the numbers 0 through -165.function y = fcn(u) %#codegen y = log2(u); end
On the Simulation > Step Back > Configure simulation stepping pane:
Select Enable stepping back.
Select Pause simulation when time reaches and enter
121.
In the model window, run the simulation. The simulation pauses at
T=121. The displayed values:ConditionRealScalaroutput approaches zero.Repeating Sequence Stair outputapproaches zero.
Step the simulation forward to
T=127.ConditionRealScalarflushes the subnormal value output fromRepeating Sequence Stairto zero.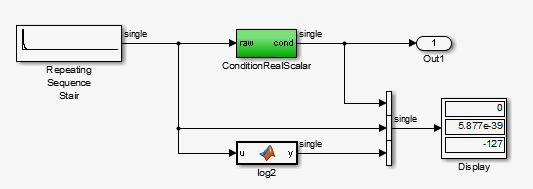
Continue stepping the simulation forward.
ConditionRealScalarflushes the subnormal single precision values output fromRepeating Sequence Stairto zero. WhenT=150, the output ofRepeating Squence Stairis itself zero.