Optimize Nonsmooth Function Using patternsearch, Problem-Based

This example shows how to minimize a nonsmooth function using direct search in the problem-based approach. The function to minimize, ps_example(x), is included when you run this example.

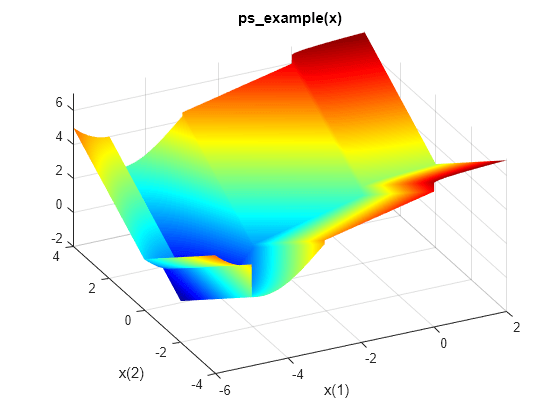
Plot the objective function.

fsurf(@(x,y)reshape(ps_example([x(:),y(:)]),size(x)),...
    [-6 2 -4 4],"LineStyle","none","MeshDensity",300)
colormap 'jet'
view(-26,43)
xlabel("x(1)")
ylabel("x(2)")
title("ps\_example(x)")

Create a 2-D optimization variable x. The ps_example function expects the variable to be a row vector, so specify x as a 2-element row vector.

x = optimvar("x",1,2);

To use ps_example as the objective function, convert the function to an optimization expression using fcn2optimexpr.

fun = fcn2optimexpr(@ps_example,x);

Create an optimization problem with objective function ps_example.

prob = optimproblem("Objective",fun);

Specify the initial point x0 as a structure with field x taking the value [2.1 1.7].

x0.x = [2.1 1.7];

Solve the problem, specifying the patternsearch solver.

[sol,fval] = solve(prob,x0,"Solver","patternsearch")

Solving problem using patternsearch.
patternsearch stopped because the mesh size was less than options.MeshTolerance.

sol = struct with fields:
    x: [-4.7124 -7.6294e-07]

fval = 
-2.0000

patternsearch finds a better solution (lower function value) than the default fminunc solver, which is not recommended for minimizing nonsmooth functions.

[solfminunc,fvalfminunc] = solve(prob,x0)

Solving problem using fminunc.

Local minimum possible.

fminunc stopped because it cannot decrease the objective function
along the current search direction.

<stopping criteria details>

solfminunc = struct with fields:
    x: [1.9240 8.8818e-16]

fvalfminunc = 
2.9161