Rectangular, Triangular, Trapezoidal, and Harmonic Loads
Model rectangular, triangular, trapezoidal, and harmonic loads by creating the helper functions. By using different parameters, such as start, rise, fall, and end times and also frequency and phase, you can model a variety of loads.
Rectangular, Triangular, and Trapezoidal Pulses
Model a trapezoidal pulse load by specifying its magnitude and a set of times.

Define a trapezoidal pulse function, trapezoidalLoad, to model a
trapezoidal load. This function accepts the load magnitude, the
location and state structure arrays, and the
function specifying the pulse parameters that define the start, rise, fall, and end
times. Because the function depends on time, it must return a matrix of
NaN of the correct size when state.time is
NaN. Solvers check whether a problem is nonlinear or
time-dependent by passing NaN state values and looking for returned
NaN values.
function Tn = trapezoidalLoad(load,location,state,T) if isnan(state.time) Tn = NaN*(location.nx); return end if isa(load,"function_handle") load = load(location,state); else load = load(:); end % Four time-points that define a trapezoidal pulse T1 = T(1); % Start time T2 = T(2); % Rise time T3 = T(3); % Fall time T4 = T(4); % End time % Determine multiplicative factor for the specified time TnTrap = max([ min([(state.time - T1)/(T2-T1), ... 1, ... (T4 - state.time)/(T4-T3)]), ... 0]); Tn = load.* TnTrap; end
The setUpTrapezoid helper function accepts the name-value arguments
StartTime, RiseTime,
FallTime, and EndTime and processes these
parameters for use in the trapezoidalLoad function. Pass the output
of this function as the last argument of trapezoidalLoad. The default
StartTime, RiseTime, and
FallTime values are 0, while the default
EndTime value is Inf.
function T = setUpTrapezoid(opts) arguments opts.StartTime double {mustBeScalarOrEmpty,mustBeReal} = [] opts.RiseTime double {mustBeScalarOrEmpty,mustBeReal} = [] opts.FallTime double {mustBeScalarOrEmpty,mustBeReal} = [] opts.EndTime double {mustBeScalarOrEmpty,mustBeReal} = [] end if isempty(opts.StartTime) opts.StartTime = 0; end if isempty(opts.RiseTime) opts.RiseTime = 0; end if isempty(opts.FallTime) opts.FallTime = 0; end if isempty(opts.EndTime) && (opts.FallTime ~= 0) opts.EndTime = opts.StartTime + opts.RiseTime + opts.FallTime; elseif isempty(opts.EndTime) && (opts.FallTime == 0) opts.EndTime = Inf; end T = [opts.StartTime; opts.StartTime + opts.RiseTime; opts.EndTime - opts.FallTime; opts.EndTime]; end
As an example, apply a trapezoidal pressure load on face 1 by using these functions.
load = 5e6; T = setUpTrapezoid(StartTime=1, ... RiseTime=0.5, ... FallTime=0.5, ... EndTime=3); pressurePulse = @(location,state) ... trapezoidalLoad(load,location,state,T); model.FaceLoad(1) = faceLoad(Pressure=pressurePulse);
For rectangular and triangular pulses, use the same helper functions and specify start, rise, fall, and end times as follows:
For a rectangular pulse, specify the start and end times.
For a triangular pulse, specify the start time and any two of these times: rise time, fall time, and end time. You also can specify all four times, but they must be consistent.
Harmonic Load
Model a harmonic load by specifying its magnitude, frequency, and phase.
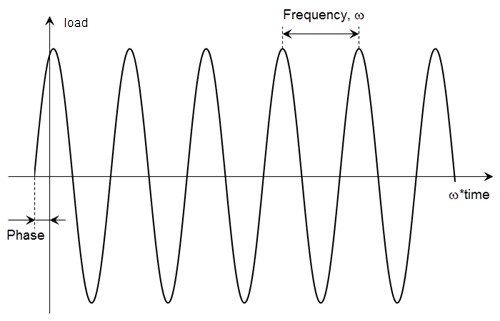
Define a sinusoidal load function, sinusoidalScalarLoad, to model a
harmonic load. This function accepts the load magnitude (amplitude), the
location and state structure arrays,
frequency, and phase. Because the function depends on time, it must return a matrix of
NaN of the correct size when state.time is
NaN. Solvers check whether a problem is nonlinear or
time-dependent by passing NaN state values and looking for returned
NaN values.
function Tn = sinusoidalScalarLoad(load,location,state,Frequency,Phase) if isnan(state.time) Tn = NaN*(location.nx); return end if isa(load,"function_handle") load = load(location,state); else load = load(:); end % Transient model excited with harmonic load Tn = load.*sin(Frequency.*state.time + Phase); end
As an example, apply a sinusoidal pressure load on face 1 by using the
sinusoidalScalarLoad function.
Pressure = 5e7;
Frequency = 25;
Phase = 0;
pressurePulse = @(location,state) ...
sinusoidalScalarLoad(Pressure,location,state,Frequency,Phase);
model.FaceLoad(1) = faceLoad(Pressure=pressurePulse);You can also define a sinusoidal load function depending on all three coordinates. Use this function to specify loads whose values must be vectors, such as force, surface traction, and so on. Do not use it for loads specified as scalars, such as heat, pressure, and so on.
function Tn = sinusoidalVectorLoad(load,location,state,Frequency,Phase) if isnan(state.time) normal = [location.nx location.ny]; if isfield(location,"nz") normal = [normal location.nz]; end Tn = NaN*normal; return end if isa(load,"function_handle") load = load(location,state); else load = load(:); end % Transient model excited with harmonic load Tn = load.*sin(Frequency.*state.time + Phase); end