Position Delta Robot Using Generalized Inverse Kinematics
Model a delta robot using the a rigidBodyTree robot model. Specify kinematic constraints for generalized inverse kinematics (GIK) to ensure the proper behavior of the robot. Solve for joint configurations that obey the defined model and constraints.
Create Delta Robot
Normally, delta robots contain closed-loop kinematic chains. The rigidBodyTree object does not support closed-loop chains. To avoid this, the robot is modeled as a tree, with the arms of the delta robot remaining unconnected. Call the helper function which builds the robot model and outputs the rigidBodyTree object.
In a subsequent step, the generalized inverse kinematics solver will apply constraints that force the separate arms of the tree to move together, thereby ensuring that the robot behaves in a kinematically accurate manner.
The robot is fairly complicated, so a helper function is used to create the rigidBodyTree object.
robot = exampleHelperDeltaRobot; show(robot);
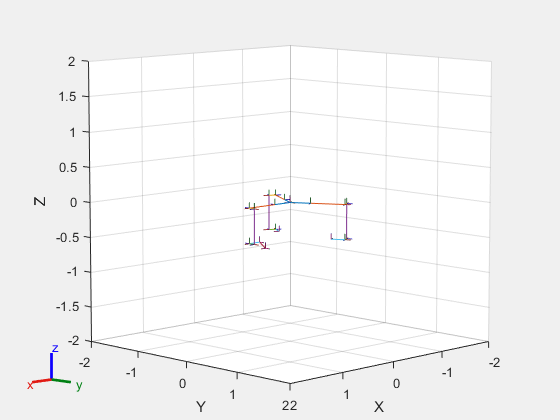
As shown, the robot consists of three arms, but they still need to be connected to match the classic delta robot configuration.
Create Inverse Kinematic Constraints
Create a generalizedInverseKinematics object, and specify the robot model. Limit the maximum number of interations based on performance.
gik1 = generalizedInverseKinematics('RigidBodyTree', robot);
gik1.SolverParameters.MaxIterations = 20;Create an interactiveRigidBodyTree object to visualize the robot model and provide interactive markers for moving bodies. This interactivity helps verify your kinematic constraints. Specify the gik1 solver using name-value pairs. Specify a pose weight vector that only focuses on the xyz-position and not the orientation.
viztree = interactiveRigidBodyTree(robot, 'IKSolver', gik1, 'SolverPoseWeights', [0 1]);
Using this interactive object, the end effector can be dragged around to show how the robot moves. Currently, the behavior is not as desired for a normal delta robot.
Store the current axes.
ax = gca;
Add constraints to the GIK solver to ensure that the arms are connected. Attach the two arms with no end effector to the 6th body of the primary arm which includes the end effector.
% Ensure that the body 6 of arm 2 maintains a pose relative to body 6 of arm 1 poseTgt1 = constraintPoseTarget('arm2_body6'); poseTgt1.ReferenceBody = 'arm1_body6'; poseTgt1.TargetTransform = trvec2tform([-sqrt(3)*0.5*0.2, 0.5*0.2, 0]) * eul2tform([2*pi/3, 0, 0]); % Ensure that the body 6 of arm 3 maintains a pose relative to body 6 of arm 1 poseTgt2 = constraintPoseTarget('arm3_body6'); poseTgt2.ReferenceBody = 'arm1_body6'; poseTgt2.TargetTransform = trvec2tform([-sqrt(3)*0.5*0.2, -0.5*0.2, 0]) * eul2tform([-2*pi/3, 0, 0]);
To apply these constraints to the robot, call addConstraint to the vizTree object.
addConstraint(viztree,poseTgt1); addConstraint(viztree,poseTgt2);

Now when the end effector is moved around, the constraints are respected and the arms stay connected.
Solve Generalized Inverse Kinematics Programmatically
The interactive visualization is useful for validating the solver constraints, but for direct programmatic use, create a separate GIK solver that can be called. This solver can be copied from the IKSolver property of the interactiveRigidBodyTree object, or created independently.
gik2 = generalizedInverseKinematics('RigidBodyTree', robot);
gik2.SolverParameters.MaxIterations = 20;For the GIK solver, an additional constraint is required to define the end effector position, which is normally controlled by the interactive marker. Update the TargetTransform to solve for different desired end-effector positions.
poseTgt3 = constraintPoseTarget('endEffector'); poseTgt3.ReferenceBody = 'base'; poseTgt3.TargetTransform = trvec2tform([0, 0, -1]);
Specify all the constraint types used by the solver.
gik2.ConstraintInputs = {'pose','pose', 'pose'};Call the gik2 solver with the specified pose target constraint objects. Give an initial guess of the home configuration of the robot. Show the solution.
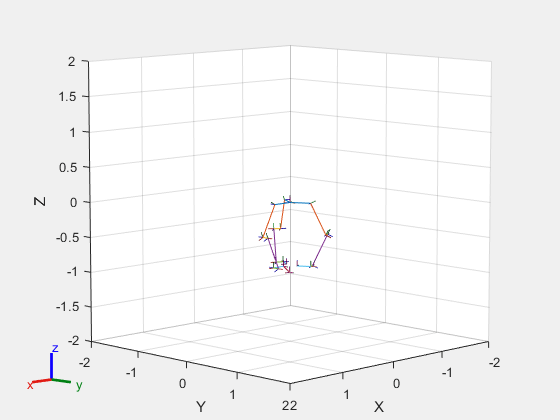
% Provide an initial guess for the solver q0 = homeConfiguration(robot); % Solve for a the target pose given to poseTgt3 [q, solutionInfo] = gik2(q0, poseTgt1, poseTgt2, poseTgt3); % Visualize the results figure; show(robot, q);
See Also
generalizedInverseKinematics | constraintPositionTarget