Specify PI-D and I-PD Controllers
PI-D and I-PD controllers are used to mitigate the influence of changes in the reference signal on the control signal. These controllers are variants of the 2DOF PID controller.
The general formula of a parallel-form 2DOF PID controller is:
Here, r and y are the reference input and measured output, respectively. u is the controller output, also called the control signal. P, I, and D specify the proportional, integral, and derivative gains, respectively. N specifies the derivative filter coefficient. b and c specify setpoint weights for the proportional and derivative components, respectively. For a 1DOF PID controller, b and c are equal to 1.
If r is nonsmooth or discontinuous, the derivative and proportional components can contribute large spikes or offsets in u, which can be infeasible. For example, a step input can lead to a large spike in u because of the derivative component. For a motor actuator, such an aggressive control signal could damage the motor.
To mitigate the influence of r on u, set b or c, or both, to 0. Use one of the following setpoint-weight-based forms:
PI-D (b = 1 and c = 0) — Derivative component does not directly propagate changes in r to u, whereas the proportional component does. However, the derivative component, which has a greater impact, is suppressed. Also referred to as the derivative of output controller.
The general formula for this controller form is:
I-PD (b = 0 and c = 0) — Proportional and derivative components do not directly propagate changes in r to u.
The general formula for this controller form is:
You can tune the P, I, D, and N coefficients of a PI-D or I-PD controller to achieve the desired disturbance rejection and reference tracking.
Simulate PI-D and I-PD Controllers in Simulink
To specify a PI-D or I-PD controller using the PID Controller (2DOF) or Discrete PID Controller (2DOF) blocks, open the block and set the Controller parameter to PID.
For a PI-D controller, set the Setpoint weight (b) parameter to
1and the Setpoint weight (c) parameter to0.For an I-PD controller, set the Setpoint weight (b) parameter to 0 and the Setpoint weight (c) parameter to
0.
Open the pid2dof_setpoint_based_controllers model, which compares the performance of a 1DOF PID, a PI-D, and an I-PD controller. The model uses the same P, I, and D parameters for all three controllers
mdl = "pid2dof_setpoint_based_controllers";
open_system(mdl)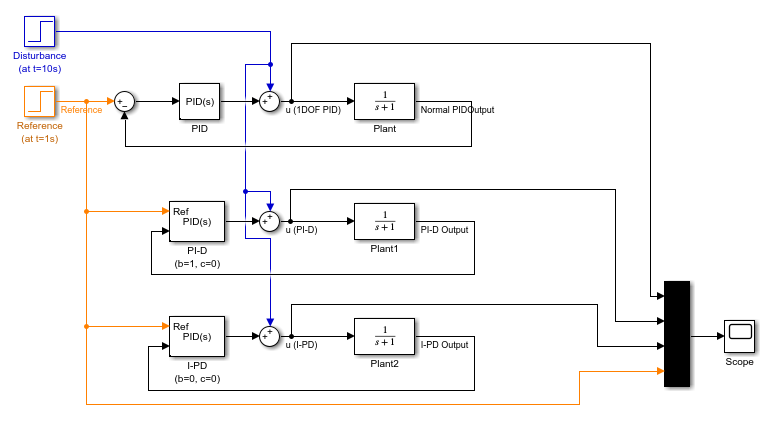
Simulate the model and view the results.
sim(mdl)
open_system(mdl + "/Scope")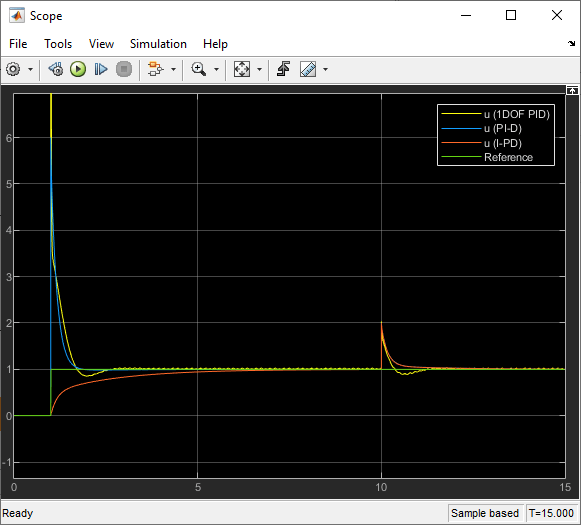
All of the controllers reject the disturbance equally well. The 1DOF PID controller results in a large spike when the reference changes from 0 to 1. The PI-D form results in a smaller jump. In contrast, the I-PD form does not react as much to the reference change.
Automatic Tuning of PI-D and I-PD Controllers
You can use PID Tuner to automatically tune PI-D and I-PD controllers while preserving the fixed b and c values. To do so:
In the model, open the block. In the block dialog box, in the Controller menu, select
PID.Click Tune. PID Tuner opens.
In PID Tuner, in the Type menu, select
PI-DForI-PDF. PID Tuner retunes the controller gains, fixing b = 1 and c = 0 for PI-D, and b = 0 and c = 0 for I-PD.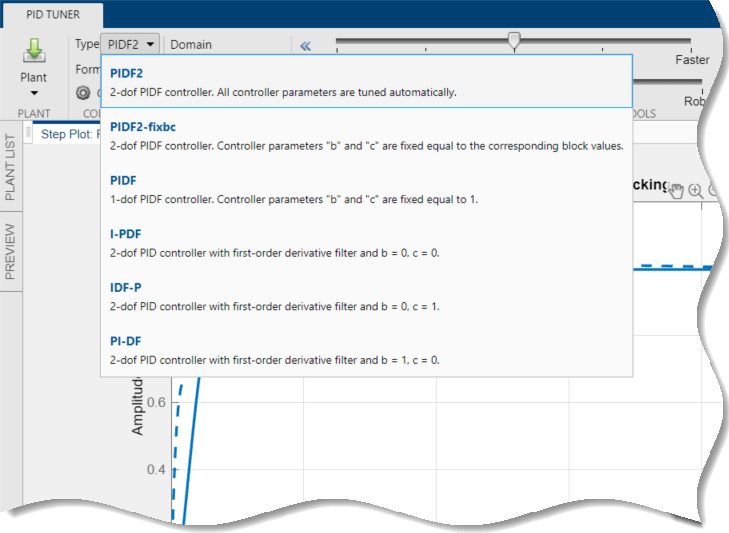
You can now analyze system responses as described in Analyze Design in PID Tuner.
See Also
PID Controller (2DOF) | Discrete PID Controller (2DOF)