Iterative Learning Control
Iterative learning control (ILC) is a control technique that is useful when you want to improve the performance of systems that execute repeated operations, starting at the same initial operating condition. This method uses frequent measurements in the form of the error trajectory from the previous batch run to update the control signal for the subsequent batch run. Applications of ILC include many practical industrial systems in manufacturing, robotics, and chemical processing, where mass production on an assembly line entails repetition. Therefore, use ILC when you have a repetitive task or repetitive disturbances and want to use knowledge from previous iteration to improve next iteration.
A general ILC update law is of the following form ([1] and [2]):
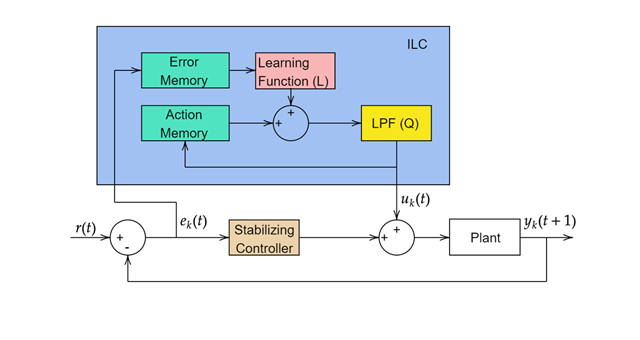
Here, Q is a low-pass filter that removes control chatter and L is a learning function. k represents the kth iteration. There are multiple ways to design the learning function.
To implement ILC in Simulink®, use the Iterative Learning Control block. Using this block, you can implement model-free or model-based ILC.
Model-Free ILC
Model-free ILC does not require prior knowledge of the system dynamics and uses proportional-derivative (PD) error feedback to update the control history. This method is applicable only to SISO systems.
The model-free ILC update law is:
Here, γp and γd are the proportion and derivative gains, respectively. Depending on the choice of gains, you can implement P-type, D-type, or PD-type ILC. The gains γp and γd determine how well ILC learns between iterations. If ILC gains are too big, it might make the closed-loop system unstable (robustness). If ILC gains are too small, it might lead to slower convergence (performance). With properly tuned ILC gains, you can achieve the nominal asymptotic convergence of the tracking error to zero.
Model-Based ILC
This method is a more general form of ILC and is applicable to SISO and MIMO LTI state-space systems of the following form:
In this method, you design a learning function L based on the plant input-output matrix G. From the plant dynamics, you can define the input-output relationship Yk = GUk + d. Here:
Additionally, you can write the error dynamics as:
The Iterative Learning Control block provides two types of model-based ILC: gradient based and inverse-model based.
Gradient-Based ILC Law
The gradient-based ILC uses the transpose of input-output matrix in the learning function L = γGT. Therefore, the ILC control law becomes:
The error dynamics are:
Here, γ is the ILC gain. The error convergence depends on the choice of gain. This method guarantees error convergence with |1 – γGGT| < 1. Therefore, for fastest convergence, you can specify γ = 1/|G2|.
Inverse-Model-Based ILC Law
The inverse-model-based ILC uses the inverse of input-output matrix in the learning function L = γG-1. Therefore, the ILC control law becomes:
When G matrix is not square, the block uses a pseudoinverse instead.
The error dynamics are:
This method guarantees error convergence with |1 – γ| < 1. Therefore, specify a positive scalar less than 2 to achieve convergence.
References
[1] Bristow, Douglas A., Marina Tharayil, and Andrew G. Alleyne. “A Survey of Iterative Learning Control.” IEEE Control Systems 26, no. 3 (June 2006): 96–114. https://doi.org/10.1109/MCS.2006.1636313.
[2] Gunnarsson, Svante, and Mikael Norrlöf. A Short Introduction to Iterative Learning Control. Linköping University Electronic Press, 1997.
[3] Hätönen, J., T.J. Harte, D.H. Owens, J. Ratcliffe, P. Lewin, and E. Rogers. “Discrete-Time Arimoto ILC-Algorithm Revisited.” IFAC Proceedings Volumes 37, no. 12 (August 2004): 541–46.
[4] Lee, Jay H., Kwang S. Lee, and Won C. Kim. “Model-Based Iterative Learning Control with a Quadratic Criterion for Time-Varying Linear Systems.” Automatica 36, no. 5 (May 1, 2000): 641–57.
[5] Harte, T. J., J. Hätönen, and D. H. Owens *. “Discrete-Time Inverse Model-Based Iterative Learning Control: Stability, Monotonicity and Robustness.” International Journal of Control 78, no. 8 (May 20, 2005): 577–86.
[6] Zhang, Yueqing, Bing Chu, and Zhan Shu. “A Preliminary Study on the Relationship Between Iterative Learning Control and Reinforcement Learning⁎.” IFAC-PapersOnLine, 13th IFAC Workshop on Adaptive and Learning Control Systems ALCOS 2019, 52, no. 29 (January 1, 2019): 314–19. https://doi.org/10.1016/j.ifacol.2019.12.669.