Modeling Data with the Generalized Extreme Value Distribution
This example shows how to fit the generalized extreme value distribution using maximum likelihood estimation. The extreme value distribution is used to model the largest or smallest value from a group or block of data.
Three types of extreme value distributions are common, each as the limiting case for different types of underlying distributions. For example, the type I extreme value is the limit distribution of the maximum (or minimum) of a block of normally distributed data, as the block size becomes large. In this example, we will illustrate how to fit such data using a single distribution that includes all three types of extreme value distributions as special case, and investigate likelihood-based confidence intervals for quantiles of the fitted distribution.
The Generalized Extreme Value Distribution
The Generalized Extreme Value (GEV) distribution unites the type I, type II, and type III extreme value distributions into a single family, to allow a continuous range of possible shapes. It is parameterized with location and scale parameters, mu and sigma, and a shape parameter, k. When k < 0, the GEV is equivalent to the type III extreme value. When k > 0, the GEV is equivalent to the type II. In the limit as k approaches 0, the GEV becomes the type I.
x = linspace(-3,6,1000); plot(x,gevpdf(x,-.5,1,0),'-', x,gevpdf(x,0,1,0),'-', x,gevpdf(x,.5,1,0),'-'); xlabel('(x-mu) / sigma'); ylabel('Probability Density'); legend({'k < 0, Type III' 'k = 0, Type I' 'k > 0, Type II'});
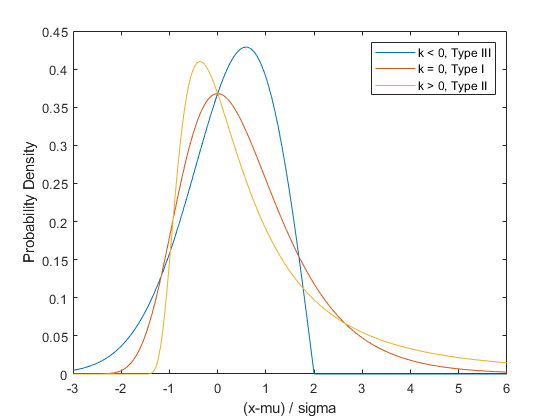
Notice that for k < 0 or k > 0, the density has zero probability above or below, respectively, the upper or lower bound -(1/k). In the limit as k approaches 0, the GEV is unbounded. This can be summarized as the constraint that 1+k*(y-mu)/sigma must be positive.
Simulating Block Maximum Data
The GEV can be defined constructively as the limiting distribution of block maxima (or minima). That is, if you generate a large number of independent random values from a single probability distribution, and take their maximum value, the distribution of that maximum is approximately a GEV.
The original distribution determines the shape parameter, k, of the resulting GEV distribution. Distributions whose tails fall off as a polynomial, such as Student's t, lead to a positive shape parameter. Distributions whose tails decrease exponentially, such as the normal, correspond to a zero shape parameter. Distributions with finite tails, such as the beta, correspond to a negative shape parameter.
Real applications for the GEV might include modeling the largest return for a stock during each month. Here, we will simulate data by taking the maximum of 25 values from a Student's t distribution with two degrees of freedom. The simulated data will include 75 random block maximum values.
rng(0,'twister');
y = max(trnd(2,25,75),[],1);
Fitting the Distribution by Maximum Likelihood
The function gevfit returns both maximum likelihood parameter estimates, and (by default) 95% confidence intervals.
[paramEsts,paramCIs] = gevfit(y); kMLE = paramEsts(1) % Shape parameter sigmaMLE = paramEsts(2) % Scale parameter muMLE = paramEsts(3) % Location parameter
kMLE =
0.4901
sigmaMLE =
1.4856
muMLE =
2.9710
kCI = paramCIs(:,1) sigmaCI = paramCIs(:,2) muCI = paramCIs(:,3)
kCI =
0.2020
0.7782
sigmaCI =
1.1431
1.9307
muCI =
2.5599
3.3821
Notice that the 95% confidence interval for k does not include the value zero. The type I extreme value distribution is apparently not a good model for these data. That makes sense, because the underlying distribution for the simulation had much heavier tails than a normal, and the type II extreme value distribution is theoretically the correct one as the block size becomes large.
As an alternative to confidence intervals, we can also compute an approximation to the asymptotic covariance matrix of the parameter estimates, and from that extract the parameter standard errors.
[nll,acov] = gevlike(paramEsts,y); paramSEs = sqrt(diag(acov))
paramSEs =
0.1470
0.1986
0.2097
Checking the Fit Visually
To visually assess how good the fit is, we'll look at plots of the fitted probability density function (PDF) and cumulative distribution function (CDF).
The support of the GEV depends on the parameter values. In this case, the estimate for k is positive, so the fitted distribution has zero probability below a lower bound.
lowerBnd = muMLE-sigmaMLE./kMLE;
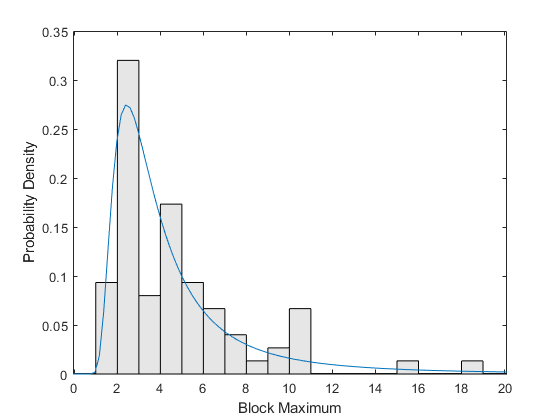
First, we'll plot a scaled histogram of the data, overlaid with the PDF for the fitted GEV model. This histogram is scaled so that the bar heights times their width sum to 1, to make it comparable to the PDF.
ymax = 1.1*max(y); bins = floor(lowerBnd):ceil(ymax); h = bar(bins,histc(y,bins)/length(y),'histc'); h.FaceColor = [.9 .9 .9]; ygrid = linspace(lowerBnd,ymax,100); line(ygrid,gevpdf(ygrid,kMLE,sigmaMLE,muMLE)); xlabel('Block Maximum'); ylabel('Probability Density'); xlim([lowerBnd ymax]);
We can also compare the fit to the data in terms of cumulative probability, by overlaying the empirical CDF and the fitted CDF.
[F,yi] = ecdf(y); plot(ygrid,gevcdf(ygrid,kMLE,sigmaMLE,muMLE),'-'); hold on; stairs(yi,F,'r'); hold off; xlabel('Block Maximum'); ylabel('Cumulative Probability'); legend('Fitted Generalized Extreme Value CDF','Empirical CDF','location','southeast'); xlim([lowerBnd ymax]);

Estimating Quantiles of the Model
While the parameter estimates may be important by themselves, a quantile of the fitted GEV model is often the quantity of interest in analyzing block maxima data.
For example, the return level Rm is defined as the block maximum value expected to be exceeded only once in m blocks. That is just the (1-1/m)'th quantile. We can plug the maximum likelihood parameter estimates into the inverse CDF to estimate Rm for m=10.
R10MLE = gevinv(1-1./10,kMLE,sigmaMLE,muMLE)
R10MLE =
9.0724
We could compute confidence limits for R10 using asymptotic approximations, but those may not be valid. Instead, we will use a likelihood-based method to compute confidence limits. This method often produces more accurate results than one based on the estimated covariance matrix of the parameter estimates.
Given any set of values for the parameters mu, sigma, and k, we can compute a log-likelihood -- for example, the MLEs are the parameter values that maximize the GEV log-likelihood. As the parameter values move away from the MLEs, their log-likelihood typically becomes significantly less than the maximum. If we look at the set of parameter values that produce a log-likelihood larger than a specified critical value, this is a complicated region in the parameter space. However, for a suitable critical value, it is a confidence region for the model parameters. The region contains parameter values that are "compatible with the data". The critical value that determines the region is based on a chi-square approximation, and we'll use 95% as our confidence level. (Note that we will actually work with the negative of the log-likelihood.)
nllCritVal = gevlike([kMLE,sigmaMLE,muMLE],y) + .5*chi2inv(.95,1)
nllCritVal = 170.3044
For any set of parameter values mu, sigma, and k, we can compute R10. Therefore, we can find the smallest R10 value achieved within the critical region of the parameter space where the negative log-likelihood is larger than the critical value. That smallest value is the lower likelihood-based confidence limit for R10.
This is difficult to visualize in all three parameter dimensions, but as a thought experiment, we can fix the shape parameter, k, we can see how the procedure would work over the two remaining parameters, sigma and mu.
sigmaGrid = linspace(.8, 2.25, 110); muGrid = linspace(2.4, 3.6); nllGrid = zeros(length(sigmaGrid),length(muGrid)); R10Grid = zeros(length(sigmaGrid),length(muGrid)); for i = 1:size(nllGrid,1) for j = 1:size(nllGrid,2) nllGrid(i,j) = gevlike([kMLE,sigmaGrid(i),muGrid(j)],y); R10Grid(i,j) = gevinv(1-1./10,kMLE,sigmaGrid(i),muGrid(j)); end end nllGrid(nllGrid>gevlike([kMLE,sigmaMLE,muMLE],y)+6) = NaN; contour(muGrid,sigmaGrid,R10Grid,6.14:.64:12.14,'LineColor','r'); hold on contour(muGrid,sigmaGrid,R10Grid,[7.42 11.26],'LineWidth',2,'LineColor','r'); contour(muGrid,sigmaGrid,nllGrid,[168.7 169.1 169.6 170.3:1:173.3],'LineColor','b'); contour(muGrid,sigmaGrid,nllGrid,[nllCritVal nllCritVal],'LineWidth',2,'LineColor','b'); hold off axis([2.4 3.6 .8 2.25]); xlabel('mu'); ylabel('sigma');

The blue contours represent the log-likelihood surface, and the bold blue contour is the boundary of the critical region. The red contours represent the surface for R10 -- larger values are to the top right, lower to the bottom left. The contours are straight lines because for fixed k, Rm is a linear function of sigma and mu. The bold red contours are the lowest and highest values of R10 that fall within the critical region. In the full three dimensional parameter space, the log-likelihood contours would be ellipsoidal, and the R10 contours would be surfaces.
Finding the lower confidence limit for R10 is an optimization problem with nonlinear inequality constraints, and so we will use the function fmincon from the Optimization Toolbox™. We need to find the smallest R10 value, and therefore the objective to be minimized is R10 itself, equal to the inverse CDF evaluated for p=1-1/m. We'll create a wrapper function that computes Rm specifically for m=10.
CIobjfun = @(params) gevinv(1-1./10,params(1),params(2),params(3));
To perform the constrained optimization, we'll also need a function that defines the constraint, that is, that the negative log-likelihood be less than the critical value. The constraint function should return positive values when the constraint is violated. We'll create an anonymous function, using the simulated data and the critical log-likelihood value. It also returns an empty value because we're not using any equality constraints here.
CIconfun = @(params) deal(gevlike(params,y) - nllCritVal, []);
Finally, we call fmincon, using the active-set algorithm to perform the constrained optimization.
opts = optimset('Algorithm','active-set', 'Display','notify', 'MaxFunEvals',500, ... 'RelLineSrchBnd',.1, 'RelLineSrchBndDuration',Inf); [params,R10Lower,flag,output] = ... fmincon(CIobjfun,paramEsts,[],[],[],[],[],[],CIconfun,opts);
Feasible point with lower objective function value found, but optimality criteria not satisfied. See output.bestfeasible..
To find the upper likelihood confidence limit for R10, we simply reverse the sign on the objective function to find the largest R10 value in the critical region, and call fmincon a second time.
CIobjfun = @(params) -gevinv(1-1./10,params(1),params(2),params(3));
[params,R10Upper,flag,output] = ...
fmincon(CIobjfun,paramEsts,[],[],[],[],[],[],CIconfun,opts);
R10Upper = -R10Upper;
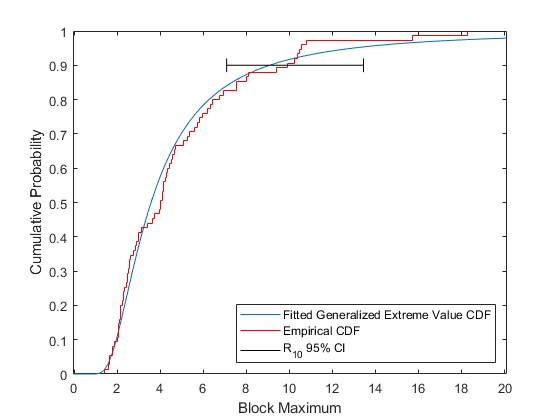
R10CI = [R10Lower, R10Upper]
R10CI =
7.0841 13.4452
plot(ygrid,gevcdf(ygrid,kMLE,sigmaMLE,muMLE),'-'); hold on; stairs(yi,F,'r'); plot(R10CI([1 1 1 1 2 2 2 2]), [.88 .92 NaN .9 .9 NaN .88 .92],'k-') hold off; xlabel('Block Maximum'); ylabel('Cumulative Probability'); legend('Fitted Generalized Extreme Value CDF','Empirical CDF', ... 'R_{10} 95% CI','location','southeast'); xlim([lowerBnd ymax]);
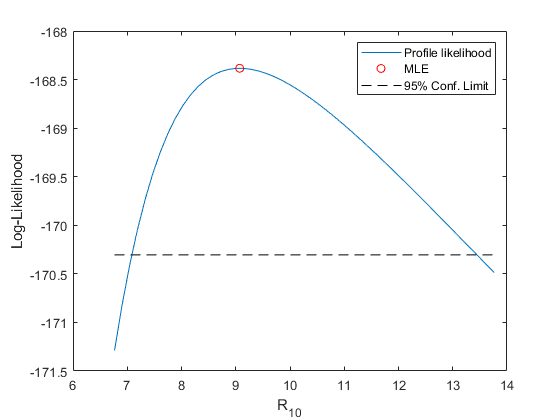
Likelihood Profile for a Quantile
Sometimes just an interval does not give enough information about the quantity being estimated, and a profile likelihood is needed instead. To find the log-likelihood profile for R10, we will fix a possible value for R10, and then maximize the GEV log-likelihood, with the parameters constrained so that they are consistent with that current value of R10. This is a nonlinear equality constraint. If we do that over a range of R10 values, we get a likelihood profile.
As with the likelihood-based confidence interval, we can think about what this procedure would be if we fixed k and worked over the two remaining parameters, sigma and mu. Each red contour line in the contour plot shown earlier represents a fixed value of R10; the profile likelihood optimization consists of stepping along a single R10 contour line to find the highest log-likelihood (blue) contour.
For this example, we'll compute a profile likelihood for R10 over the values that were included in the likelihood confidence interval.
R10grid = linspace(R10CI(1)-.05*diff(R10CI), R10CI(2)+.05*diff(R10CI), 51);
The objective function for the profile likelihood optimization is simply the log-likelihood, using the simulated data.
PLobjfun = @(params) gevlike(params,y);
To use fmincon, we'll need a function that returns non-zero values when the constraint is violated, that is, when the parameters are not consistent with the current value of R10. For each value of R10, we'll create an anonymous function for the particular value of R10 under consideration. It also returns an empty value because we're not using any inequality constraints here.
Finally, we'll call fmincon at each value of R10, to find the corresponding constrained maximum of the log-likelihood. We'll start near the maximum likelihood estimate of R10, and work out in both directions.
Lprof = nan(size(R10grid)); params = paramEsts; [dum,peak] = min(abs(R10grid-R10MLE)); for i = peak:1:length(R10grid) PLconfun = ... @(params) deal([], gevinv(1-1./10,params(1),params(2),params(3)) - R10grid(i)); [params,Lprof(i),flag,output] = ... fmincon(PLobjfun,params,[],[],[],[],[],[],PLconfun,opts); end params = paramEsts; for i = peak-1:-1:1 PLconfun = ... @(params) deal([], gevinv(1-1./10,params(1),params(2),params(3)) - R10grid(i)); [params,Lprof(i),flag,output] = ... fmincon(PLobjfun,params,[],[],[],[],[],[],PLconfun,opts); end
plot(R10grid,-Lprof,'-', R10MLE,-gevlike(paramEsts,y),'ro', ... [R10grid(1), R10grid(end)],[-nllCritVal,-nllCritVal],'k--'); xlabel('R_{10}'); ylabel('Log-Likelihood'); legend('Profile likelihood','MLE','95% Conf. Limit');