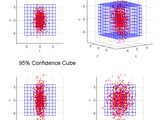
R = RCR(S) computes the semi-edge-length of the mean-centered hypercube with 95% probability given S, which is either a covariance matrix or a vector of standard deviations from a multivariate normal distribution. If S is a real, nonnegative vector, RCR(S) is equivalent to RCR(DIAG(S.^2)). Scalar S is treated as a standard deviation.
R = RCR(S,P) computes the semi-edge-length of the hypercube with probability P instead of the default, which is 0.95. R is the two-tailed, equicoordinate quantile corresponding to P. The hypercube edge-length is 2*R.
R = RCR(S,P,NP) uses NP quadrature points instead of the default, which is 2^11. Smaller values of NP result in faster computation, but may yield less accurate results. Use [] as a placeholder to obtain the default value of P.
R = RCR(S,P,NP,M) performs a bootstrap validation with M normally distributed random samples of size 1e6. Use [] as a placeholder to obtain the default value of NP.
R = RCR(S,P,NP,[M N]) performs a bootstrap validation with M normally distributed random samples of size N.
[R,E] = RCR(S,...) returns an error estimate E.
Cita come
Tom Davis (2024). Rectangular Confidence Regions (https://www.mathworks.com/matlabcentral/fileexchange/11627-rectangular-confidence-regions), MATLAB Central File Exchange. Recuperato .
Compatibilità della release di MATLAB
Compatibilità della piattaforma
Windows macOS LinuxCategorie
Tag
Riconoscimenti
Ispirato da: Confidence Region Radius
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Scopri Live Editor
Crea script con codice, output e testo formattato in un unico documento eseguibile.
| Versione | Pubblicato | Note della release | |
|---|---|---|---|
| 1.0.0.0 | updated contact information |