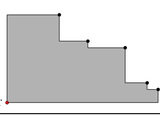
Hypervolume approximation
Approximates the hypervolume of a Pareto frontier. First, it generates
random samples in the hypercuboid defined by the utopia and antiutopia
points. Second, it counts the number of samples dominated by the front.
The hypervolume is approximated as the ratio 'dominated points / total
points'.
Please notice that the choice of the utopia and antiutopia point is
crucial: using points very far from the frontier will result in similar
hypervolume even for very different frontiers (if the utopia is too far
away, the hypervolume will be always low; if the antiutopia is too far
away, the hypervolume will be always high).
Also, frontier points "beyond" the reference points will not be counted
for the approximation (e.g., if the antiutopia is above the frontier or
the utopia is below, the hypervolume will be 0).
Inputs:
- F : the Pareto front to evaluate
- AU : antiutopia point
- U : utopia point
- N : number of sample for the approximation
Outputs:
- hv : hypervolume
Cita come
Simone (2026). Hypervolume approximation (https://it.mathworks.com/matlabcentral/fileexchange/50517-hypervolume-approximation), MATLAB Central File Exchange. Recuperato .
Compatibilità della release di MATLAB
Compatibilità della piattaforma
Windows macOS LinuxCategorie
Tag
Scopri Live Editor
Crea script con codice, output e testo formattato in un unico documento eseguibile.
| Versione | Pubblicato | Note della release | |
|---|---|---|---|
| 1.0.0.0 |