lassoglm
Lasso or elastic net regularization for generalized linear models
Syntax
Description
B = lassoglm(X,y)X and the response
y, where the values in y are assumed
to have a normal probability distribution. Each column of B
corresponds to a particular regularization coefficient in
Lambda. By default, lassoglm performs
lasso regularization using a geometric sequence of Lambda
values.
B = lassoglm(X,y,distr,Name,Value)'Alpha',0.5
sets elastic net as the regularization method, with the parameter
Alpha equal to 0.5.
Examples
Remove Redundant Predictors Using Lasso Regularization
Construct a data set with redundant predictors and identify those predictors by using lassoglm.
Create a random matrix X with 100 observations and 10 predictors. Create the normally distributed response y using only four of the predictors and a small amount of noise.
rng default X = randn(100,10); weights = [0.6;0.5;0.7;0.4]; y = X(:,[2 4 5 7])*weights + randn(100,1)*0.1; % Small added noise
Perform lasso regularization.
B = lassoglm(X,y);
Find the coefficient vector for the 75th Lambda value in B.
B(:,75)
ans = 10×1
0
0.5431
0
0.3944
0.6173
0
0.3473
0
0
0
lassoglm identifies and removes the redundant predictors.
Cross-Validated Lasso Regularization of Generalized Linear Model
Construct data from a Poisson model, and identify the important predictors by using lassoglm.
Create data with 20 predictors. Create a Poisson response variable using only three of the predictors plus a constant.
rng default % For reproducibility X = randn(100,20); weights = [.4;.2;.3]; mu = exp(X(:,[5 10 15])*weights + 1); y = poissrnd(mu);
Construct a cross-validated lasso regularization of a Poisson regression model of the data.
[B,FitInfo] = lassoglm(X,y,'poisson','CV',10);
Examine the cross-validation plot to see the effect of the Lambda regularization parameter.
lassoPlot(B,FitInfo,'plottype','CV'); legend('show') % Show legend
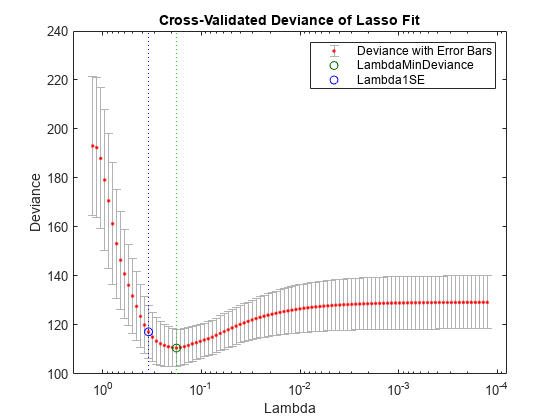
The green circle and dotted line locate the Lambda with minimum cross-validation error. The blue circle and dotted line locate the point with minimum cross-validation error plus one standard deviation.
Find the nonzero model coefficients corresponding to the two identified points.
idxLambdaMinDeviance = FitInfo.IndexMinDeviance; mincoefs = find(B(:,idxLambdaMinDeviance))
mincoefs = 7×1
3
5
6
10
11
15
16
idxLambda1SE = FitInfo.Index1SE; min1coefs = find(B(:,idxLambda1SE))
min1coefs = 3×1
5
10
15
The coefficients from the minimum-plus-one standard error point are exactly those coefficients used to create the data.
Predict Values Using Lasso Regularization
Predict whether students got a B or above on their last exam by using lassoglm.
Load the examgrades data set. Convert the last exam grades to a logical vector, where 1 represents a grade of 80 or above and 0 represents a grade below 80.
load examgrades
X = grades(:,1:4);
y = grades(:,5);
yBinom = (y>=80);Partition the data into training and test sets.
rng default % Set the seed for reproducibility c = cvpartition(yBinom,'HoldOut',0.3); idxTrain = training(c,1); idxTest = ~idxTrain; XTrain = X(idxTrain,:); yTrain = yBinom(idxTrain); XTest = X(idxTest,:); yTest = yBinom(idxTest);
Perform lasso regularization for generalized linear model regression with 3-fold cross-validation on the training data. Assume the values in y are binomially distributed. Choose model coefficients corresponding to the Lambda with minimum expected deviance.
[B,FitInfo] = lassoglm(XTrain,yTrain,'binomial','CV',3); idxLambdaMinDeviance = FitInfo.IndexMinDeviance; B0 = FitInfo.Intercept(idxLambdaMinDeviance); coef = [B0; B(:,idxLambdaMinDeviance)]
coef = 5×1
-21.1911
0.0235
0.0670
0.0693
0.0949
Predict exam grades for the test data using the model coefficients found in the previous step. Specify the link function for a binomial response using 'logit'. Convert the prediction values to a logical vector.
yhat = glmval(coef,XTest,'logit');
yhatBinom = (yhat>=0.5);Determine the accuracy of the predictions using a confusion matrix.
c = confusionchart(yTest,yhatBinom);
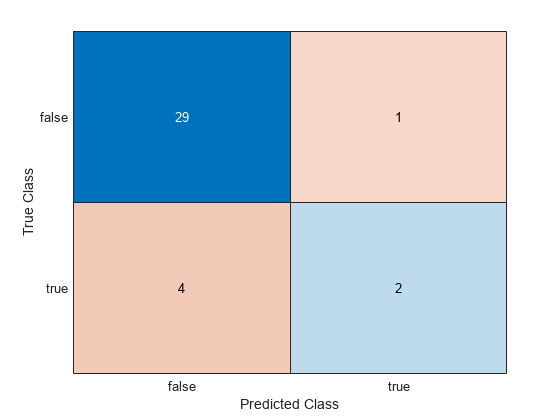
The function correctly predicts 31 exam grades. However, the function incorrectly predicts that 1 student receives a B or above and 4 students receive a grade below a B.
Use Correlation Matrix for Fitting lassoglm
Create a matrix X of N p-dimensional normal variables, where N is large and p = 1000. Create a response vector y from the model y = X*beta + noise, where beta is a vector of coefficients with 50% nonzero values.
rng default % For reproducibility N = 1e4; % Number of samples p = 1e3; % Number of features X = randn(N,p); beta = 1 + 3*rand(p,1); % Multiplicative coefficients activep = randperm(p,p/2); % 50% nonzero coefficients y = X(:,activep)*beta(activep) + randn(N,1)*0.1; % Add noise
Construct the lasso fit without using the covariance matrix. Time the creation.
B = lassoglm(X,y,"normal",UseCovariance=false); % Warm up lasso for reliable timing data tic B = lassoglm(X,y,"normal",UseCovariance=false); timefalse = toc
timefalse = 4.8752
Construct the lasso fit using the covariance matrix. Time the creation.
B2 = lassoglm(X,y,"normal",UseCovariance=true); % Warm up lasso for reliable timing data tic B2 = lassoglm(X,y,"normal",UseCovariance=true); timetrue = toc
timetrue = 1.6029
The fitting time with the covariance matrix is less than the time without it. View the speedup factor that results from using the covariance matrix.
speedup = timefalse/timetrue
speedup = 3.0415
Check that the returned coefficients B and B2 are similar.
norm(B-B2)/norm(B)
ans = 4.8056e-16
The results are virtually identical.
Input Arguments
X — Predictor data
numeric matrix
Predictor data, specified as a numeric matrix. Each row represents one observation, and each column represents one predictor variable.
Data Types: single | double
y — Response data
numeric vector | logical vector | categorical array | numeric matrix
Response data, specified as a numeric vector, logical vector, categorical array, or two-column numeric matrix.
When
distris not'binomial',yis a numeric vector or categorical array of length n, where n is the number of rows inX. The responsey(i)corresponds to row i inX.When
distris'binomial',yis one of the following:Numeric vector of length n, where each entry represents success (
1) or failure (0)Logical vector of length n, where each entry represents success or failure
Categorical array of length n, where each entry represents success or failure
Two-column numeric matrix, where the first column contains the number of successes for each observation and the second column contains the total number of trials
Data Types: single | double | logical | categorical
distr — Distribution of response data
'normal' (default) | 'binomial' | 'poisson' | 'gamma' | 'inverse gaussian'
Distribution of response data, specified as one of the following:
'normal'(default)'binomial''poisson''gamma''inverse gaussian'
lassoglm uses the default link function corresponding to distr.
Specify another link function using the Link name-value
pair argument.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: lassoglm(X,y,'poisson','Alpha',0.5) performs elastic
net regularization assuming that the response values are Poisson distributed. The
'Alpha',0.5 name-value pair argument sets the parameter used
in the elastic net optimization.
Alpha — Weight of lasso versus ridge optimization
1 (default) | positive scalar
Weight of lasso (L1)
versus ridge (L2)
optimization, specified as the comma-separated pair consisting of
'Alpha' and a positive scalar value in the
interval (0,1]. The value
Alpha = 1 represents lasso regression,
Alpha close to 0 approaches
ridge regression, and other values represent elastic net optimization.
See Elastic Net.
Example: 'Alpha',0.75
Data Types: single | double
CacheSize — Size of covariance matrix in megabytes
1000 (default) | positive scalar | 'maximal'
Size of the covariance matrix in megabytes, specified as a positive scalar or 'maximal'. The lassoglm function can use a covariance matrix for fitting when the UseCovariance argument is true or 'auto'.
If UseCovariance is true or 'auto' and CacheSize is 'maximal', lassoglm can attempt to allocate a covariance matrix that exceeds the available memory. In this case, MATLAB® issues an error.
Example: 'CacheSize','maximal'
Data Types: double | char | string
CV — Cross-validation specification for estimating deviance
'resubstitution' (default) | positive integer scalar | cvpartition object
Cross-validation specification for estimating the deviance, specified
as the comma-separated pair consisting of 'CV' and
one of the following:
'resubstitution'—lassoglmusesXandyto fit the model and to estimate the deviance without cross-validation.Positive scalar integer
K—lassoglmusesK-fold cross-validation.cvpartitionobjectcvp—lassoglmuses the cross-validation method expressed incvp. You cannot use a'leaveout'or custom'holdout'partition withlassoglm.
Example: 'CV',10
DFmax — Maximum number of nonzero coefficients
Inf (default) | positive integer scalar
Maximum number of nonzero coefficients in the model, specified as the
comma-separated pair consisting of 'DFmax' and a
positive integer scalar. lassoglm returns results
only for Lambda values that satisfy this
criterion.
Example: 'DFmax',25
Data Types: single | double
Lambda — Regularization coefficients
nonnegative vector
Regularization coefficients, specified as the comma-separated pair
consisting of 'Lambda' and a vector of nonnegative
values. See Lasso.
If you do not supply
Lambda, thenlassoglmestimates the largest value ofLambdathat gives a nonnull model. In this case,LambdaRatiogives the ratio of the smallest to the largest value of the sequence, andNumLambdagives the length of the vector.If you supply
Lambda, thenlassoglmignoresLambdaRatioandNumLambda.If
Standardizeistrue, thenLambdais the set of values used to fit the models with theXdata standardized to have zero mean and a variance of one.
The default is a geometric sequence of NumLambda
values, with only the largest value able to produce
B = 0.
Data Types: single | double
LambdaRatio — Ratio of smallest to largest Lambda values
1e–4 (default) | positive scalar
Ratio of the smallest to the largest Lambda
values when you do not supply Lambda, specified as
the comma-separated pair consisting of 'LambdaRatio'
and a positive scalar.
If you set LambdaRatio = 0, then
lassoglm generates a default sequence of
Lambda values and replaces the smallest one
with 0.
Example: 'LambdaRatio',1e–2
Data Types: single | double
Link — Mapping between mean of response and linear predictor
'comploglog' | 'identity' | 'log' | 'logit' | 'loglog' | ...
Mapping between the mean µ of the response and the
linear predictor Xb, specified as the comma-separated
pair consisting of 'Link' and one of the values in
this table.
| Value | Description |
|---|---|
'comploglog' | log(–log((1 – µ))) = Xb |
| µ = Xb |
| log(µ) = Xb |
| log(µ/(1 – µ)) = Xb |
| log(–log(µ)) = Xb |
'probit' | Φ–1(µ) = Xb, where Φ is the normal (Gaussian) cumulative distribution function |
'reciprocal', default for the distribution 'gamma' | µ–1 = Xb |
| µp = Xb |
A structure of function handles with the field | User-specified link function (see Custom Link Function) |
Example: 'Link','probit'
Data Types: char | string | single | double | cell
MaxIter — Maximum number of iterations allowed
1e4 (default) | positive integer scalar
Maximum number of iterations allowed, specified as the comma-separated
pair consisting of 'MaxIter' and a positive integer
scalar.
If the algorithm executes MaxIter iterations
before reaching the convergence tolerance RelTol,
then the function stops iterating and returns a warning message.
The function can return more than one warning when
NumLambda is greater than
1.
Example: 'MaxIter',1e3
Data Types: single | double
MCReps — Number of Monte Carlo repetitions for cross-validation
1 (default) | positive integer scalar
Number of Monte Carlo repetitions for cross-validation, specified as
the comma-separated pair consisting of 'MCReps' and a
positive integer scalar.
If
CVis'resubstitution'or acvpartitionof type'resubstitution', thenMCRepsmust be1.If
CVis acvpartitionof type'holdout', thenMCRepsmust be greater than1.If
CVis a customcvpartitionof type'kfold', thenMCRepsmust be1.
Example: 'MCReps',2
Data Types: single | double
NumLambda — Number of Lambda values
100 (default) | positive integer scalar
Number of Lambda values
lassoglm uses when you do not supply
Lambda, specified as the comma-separated pair
consisting of 'NumLambda' and a positive integer
scalar. lassoglm can return fewer than
NumLambda fits if the deviance of the fits
drops below a threshold fraction of the null deviance (deviance of the
fit without any predictors X).
Example: 'NumLambda',150
Data Types: single | double
Offset — Additional predictor variable
numeric vector
Additional predictor variable, specified as the comma-separated pair
consisting of 'Offset' and a numeric vector with the
same number of rows as X. The
lassoglm function keeps the coefficient value
of Offset fixed at 1.0.
Data Types: single | double
Options — Options for computing in parallel and setting random streams
structure
Options for computing in parallel and setting random streams, specified as a
structure. Create the Options structure using statset. This table lists the option fields and their
values.
| Field Name | Value | Default |
|---|---|---|
UseParallel | Set this value to true to run computations in
parallel. | false |
UseSubstreams | Set this value to To compute
reproducibly, set | false |
Streams | Specify this value as a RandStream object or
cell array of such objects. Use a single object except when the
UseParallel value is true
and the UseSubstreams value is
false. In that case, use a cell array that
has the same size as the parallel pool. | If you do not specify Streams, then
lassoglm uses the default stream or
streams. |
Note
You need Parallel Computing Toolbox™ to run computations in parallel.
Example: Options=statset(UseParallel=true,UseSubstreams=true,Streams=RandStream("mlfg6331_64"))
Data Types: struct
PredictorNames — Names of predictor variables
{} (default) | string array | cell array of character vectors
Names of the predictor variables, in the order in which they appear in
X, specified as the comma-separated pair
consisting of 'PredictorNames' and a string array or
cell array of character vectors.
Example: 'PredictorNames',{'Height','Weight','Age'}
Data Types: string | cell
RelTol — Convergence threshold for coordinate descent algorithm
1e–4 (default) | positive scalar
Convergence threshold for the coordinate descent algorithm [3], specified as the comma-separated pair
consisting of 'RelTol' and a positive scalar. The
algorithm terminates when successive estimates of the coefficient vector
differ in the L2 norm by a
relative amount less than RelTol.
Example: 'RelTol',2e–3
Data Types: single | double
Standardize — Flag for standardizing predictor data before fitting models
true (default) | false
Flag for standardizing the predictor data X
before fitting the models, specified as the comma-separated pair
consisting of 'Standardize' and either
true or false. If
Standardize is true, then
the X data is scaled to have zero mean and a
variance of one. Standardize affects whether the
regularization is applied to the coefficients on the standardized scale
or the original scale. The results are always presented on the original
data scale.
Example: 'Standardize',false
Data Types: logical
UseCovariance — Indication to use covariance matrix for fitting
'auto' (default) | logical scalar
Indication to use a covariance matrix for fitting, specified as
'auto' or a logical scalar.
'auto'causeslassoglmto attempt to use a covariance matrix for fitting when the number of observations is greater than the number of problem variables,Link='identity', anddistr='normal'. This attempt can fail when memory is insufficient. To find out whetherlassoglmused a covariance matrix for fitting, examine theUseCovariancefield of theFitInfooutput.truecauseslassoglmto use a covariance matrix for fitting as long as the required size does not exceedCacheSize. If the required covariance matrix size exceedsCacheSize,lassoglmissues a warning and does not use a covariance matrix for fitting.falsecauseslassoglmnot to use a covariance matrix for fitting.
Using a covariance matrix for fitting can be faster than not using one, especially for a normally-distributed response, but can require more memory. See Use Correlation Matrix for Fitting lassoglm. The speed increase can negatively affect numerical stability. For details, see Coordinate Descent Algorithm.
Example: 'UseCovariance',true
Data Types: logical | char | string
Weights — Observation weights
1/n*ones(n,1) (default) | nonnegative vector
Observation weights, specified as the comma-separated pair consisting
of 'Weights' and a nonnegative vector.
Weights has length n, where
n is the number of rows of
X. At least two values must be positive.
Data Types: single | double
Output Arguments
B — Fitted coefficients
numeric matrix
Fitted coefficients, returned as a numeric matrix. B
is a p-by-L matrix, where
p is the number of predictors (columns) in
X, and L is the number of
Lambda values. You can specify the number of
Lambda values using the
NumLambda name-value pair argument.
The coefficient corresponding to the intercept term is a field in
FitInfo.
Data Types: single | double
FitInfo — Fit information of models
structure
Fit information of the generalized linear models, returned as a structure with the fields described in this table.
Field in
FitInfo | Description |
|---|---|
Intercept | Intercept term
β0 for each
linear model, a 1-by-L
vector |
Lambda | Lambda parameters in ascending order, a
1-by-L
vector |
Alpha | Value of the Alpha parameter, a
scalar |
DF | Number of nonzero coefficients in B
for each value of Lambda, a
1-by-L
vector |
Deviance | Deviance of the fitted model for each value of
If the model is cross-validated, then
the values for |
PredictorNames | Value of the PredictorNames parameter,
stored as a cell array of character vectors |
UseCovariance | Logical value indicating whether the covariance matrix
was used in fitting. If the covariance was computed and
used, this field is true. Otherwise, this
field is false. |
If you set the CV name-value pair argument to
cross-validate, the FitInfo structure contains these
additional fields.
Field in
FitInfo | Description |
|---|---|
SE | Standard error of Deviance for each
Lambda, as calculated during
cross-validation, a
1-by-L
vector |
LambdaMinDeviance | Lambda value with minimum expected
deviance, as calculated by cross-validation, a
scalar |
Lambda1SE | Largest Lambda value such that
Deviance is within one standard error
of the minimum, a scalar |
IndexMinDeviance | Index of Lambda with the value
LambdaMinDeviance, a scalar |
Index1SE | Index of Lambda with the value
Lambda1SE, a scalar |
More About
Link Function
A link function f(μ) maps a distribution with mean μ to a linear model with data X and coefficient vector b using the formula
f(μ) = Xb.
You can find the formulas for the link functions in the Link
name-value pair argument description. This table lists the link functions that are
typically used for each distribution.
| Distribution Family | Default Link Function | Other Typical Link Functions |
|---|---|---|
'normal' | 'identity' | |
'binomial' | 'logit' | 'comploglog', 'loglog',
'probit' |
'poisson' | 'log' | |
'gamma' | 'reciprocal' | |
'inverse gaussian' | –2 |
Lasso
For a nonnegative value of λ, lassoglm solves the
problem
The function Deviance in this equation is the deviance of the model fit to the responses using the intercept β0 and the predictor coefficients β. The formula for Deviance depends on the
distrparameter you supply tolassoglm. Minimizing the λ-penalized deviance is equivalent to maximizing the λ-penalized loglikelihood.N is the number of observations.
λ is a nonnegative regularization parameter corresponding to one value of
Lambda.The parameters β0 and β are a scalar and a vector of length p, respectively.
As λ increases, the number of nonzero components of β decreases.
The lasso problem involves the L1 norm of β, as contrasted with the elastic net algorithm.
Elastic Net
For α strictly between 0 and 1, and nonnegative λ, elastic net solves the problem
where
Elastic net is the same as lasso when α = 1. For other values of α,
the penalty term Pα(β)
interpolates between the L1 norm
of β and the squared L2 norm
of β. As α shrinks
toward 0, elastic net approaches ridge regression.
Algorithms
Coordinate Descent Algorithm
lassoglm fits many values of λ
simultaneously by an efficient procedure named coordinate
descent, based on Friedman, Tibshirani, and Hastie [3]. The procedure has two main code paths depending on whether the fitting uses a
covariance matrix. You can affect this choice with the
UseCovariance name-value argument.
When lassoglm uses a covariance matrix to fit
N data points and D predictors, the
fitting has a rough computational complexity of D*D. Without a
covariance matrix, the computational complexity is roughly N*D.
So, typically, using a covariance matrix can be faster when N >
D, and the default 'auto' setting of the
UseCovariance argument makes this choice. Using a covariance
matrix causes lassoglm to subtract larger numbers than
otherwise, which can be less numerically stable. For details of the algorithmic
differences, see [3]. For one comparison of timing and accuracy
differences, see Use Correlation Matrix for Fitting lassoglm.
References
[1] Tibshirani, R. “Regression Shrinkage and Selection via the Lasso.” Journal of the Royal Statistical Society. Series B, Vol. 58, No. 1, 1996, pp. 267–288.
[2] Zou, H., and T. Hastie. “Regularization and Variable Selection via the Elastic Net.” Journal of the Royal Statistical Society. Series B, Vol. 67, No. 2, 2005, pp. 301–320.
[3] Friedman, J., R. Tibshirani, and T. Hastie.
“Regularization Paths for Generalized Linear Models via Coordinate
Descent.” Journal of Statistical Software. Vol. 33, No. 1,
2010. https://www.jstatsoft.org/v33/i01
[4] Hastie, T., R. Tibshirani, and J. Friedman. The Elements of Statistical Learning. 2nd edition. New York: Springer, 2008.
[5] Dobson, A. J. An Introduction to Generalized Linear Models. 2nd edition. New York: Chapman & Hall/CRC Press, 2002.
[6] McCullagh, P., and J. A. Nelder. Generalized Linear Models. 2nd edition. New York: Chapman & Hall/CRC Press, 1989.
[7] Collett, D. Modelling Binary Data. 2nd edition. New York: Chapman & Hall/CRC Press, 2003.
Extended Capabilities
Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2012a
Comando MATLAB
Hai fatto clic su un collegamento che corrisponde a questo comando MATLAB:
Esegui il comando inserendolo nella finestra di comando MATLAB. I browser web non supportano i comandi MATLAB.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)