Control System Tuning in Simulink Made Easy
By Pascal Gahinet and Arkadiy Turevskiy, MathWorks
As control engineers know, tuning a control system can be challenging when you must rely on hand-tuning and experience. This is especially true for control systems with multiple feedback loops or tunable components, such as cascaded PID loops, control structures with feedforward and feedback action, and MIMO control loops with significant cross-coupling. Traditionally, engineers tune one element or one control loop at a time. In addition to being iterative and time-consuming, this method requires expertise, is difficult for new engineers to master, and does not guarantee an optimal final design.
Using a helicopter flight control system as an example, this article describes a systematic and automated method for tuning all controller parameters at once subject to standard performance and robustness requirements.
Helicopter Flight Control System: Architecture and Requirements
Figure1 shows the helicopter flight control system modeled in Simulink®. Helicopter dynamics are modeled in the “Helicopter” block. The flight control system generates commands ds, dc, and dT in degrees for the longitudinal cyclic, lateral cyclic, and tail rotor collective, respectively, using measurements of theta (pitch angle), phi (roll angle), and p, q, and r (roll, pitch, and yaw rates). The controller consists of two feedback loops. The inner loop (the static output feedback block, light blue in Figure 1) provides stability augmentation and decoupling. The outer loop (the PI blocks, orange in Figure 1) provides the desired setpoint tracking performance.
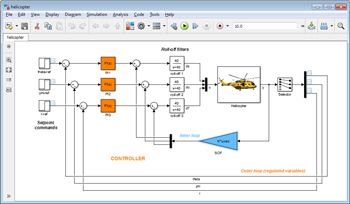
The requirements for the control system are as follows:
- Track setpoint changes in theta, phi, and r with zero steady-state error, settling times of about two seconds, minimal overshoot, and minimal cross-coupling.
- Provide strong multivariable gain and phase margins.
- Limit the closed-loop system bandwidth to guard against neglected high-frequency rotor dynamics and measurement noise.
The flight control system uses lowpass filters with cutoff at 40 rad/s to partially enforce the third objective.
Controller Tuning Challenge
The control system has 21 tunable parameters: six gains for the three PI controllers in the outer loop, and 15 values for the 3-by-5 gain matrix in the inner loop. All PI gains are initialized to one, and the gain matrix in the inner loop is initialized to zero. Simulating the model with these values, we see that the untuned system is unstable (Figure 2).
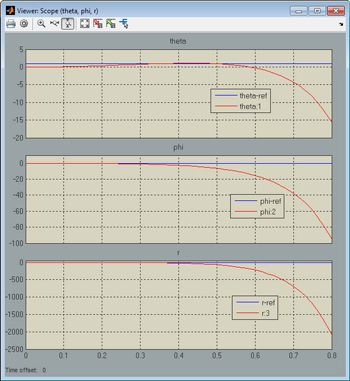
We need to tune all 21 controller parameters to stabilize the system and meet all the requirements. We use the systune command from Robust Control Toolbox™ to jointly tune the inner and outer loops.
Workflow for Automated Controller Tuning
systune tunes control systems modeled in Simulink subject to a mix of time- and frequency-domain requirements. The workflow consists of four main steps:
- Specify the blocks to tune in the Simulink model.
- Define the requirements.
- Tune the control system parameters.
- Update the Simulink blocks with the tuned values and verify the design in simulation.
Specifying the Blocks to Tune
Using the slTunable interface in Simulink Control Design™, we specify the name of the Simulink model and the names of the model blocks to tune. slTunable automatically linearizes the Simulink model and sets up the tuning task for systune.

Defining the Requirements
Robust Control Toolbox provides a comprehensive set of tuning goals, including reference tracking, disturbance rejection, loop shaping, gain and phase margins, and closed-loop pole locations. For this example we use the following requirements:
- Track setpoint changes with a response time of about two seconds and less than 1% steady-state error.

- Ensure robustness to gain variations of 5 dB and phase variations of 40 degrees at the plant inputs and outputs (independently or simultaneously in all channels).

- Limit the natural frequency of the closed-loop poles to 20 rad/s.

Tuning the Control System Parameters
We are now ready to use systune to jointly tune all 21 controller parameters. systune returns the tuned version ST1 of the control system model ST0.

The underlying optimization takes about three seconds. Figure 3 shows that the tuned controller nearly meets all four requirements.
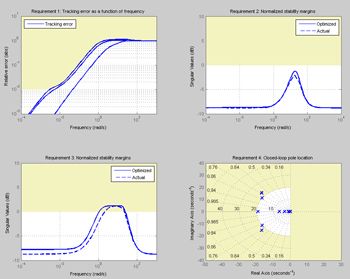
Updating and Verifying the Model
We update the Simulink model block parameters with the tuned values.

Running the simulation with these tuned parameter values confirms that the controller provides a stable response with good tracking and effective decoupling (Figure 4).
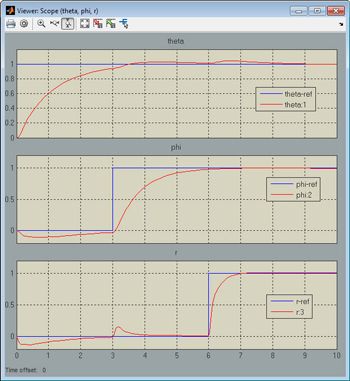
Tuning Capabilities
systune can tune most blocks used to create a control system in Simulink. These include Gain, PID Controller, Transfer Fcn, State-Space, Zero-Pole, Discrete Filter, and LTI System blocks. Any controller architecture created using these blocks can be tuned.
By adjusting the tuning requirements, we can quickly explore the tradeoffs between performance and robustness. We can also explore the benefits and drawbacks of different control architectures and controller complexity. For example, by setting the “SOF” gain to zero and retuning the PI loops with systune, we can test whether the inner feedback loop is necessary. Comparing the results with the original two-loop design suggests that the inner loop has an important stabilizing effect, and should be preserved.
We can also use systune to tune control systems against multiple plant models representing different operating conditions, nominal and degraded operating modes, or the natural variability in the system. For example, a flight control system can be tuned to meet minimal performance and stability requirements not only for the normally functioning flight vehicle but also for a set of scenarios representing various actuator and sensor failures.
While systune is designed for tuning linear controllers in the linear domain, it can also be used to tune gain-scheduled controllers for nonlinear systems, for example, a flight control system whose parameter values have to be scheduled with angle of attack and aircraft speed. systune can tune the entire gain surfaces at once and produces smooth and explicit formulae for the gain dependence on the scheduling variables.
Finally, for engineers familiar with the LQG and H-infinity design techniques, systune extends these techniques in two important ways. You can perform fixed-order and fixed-structure LQG or H-infinity synthesis, and you can optimize the control system parameters using a mix of LQG (H-2) and H-infinity objectives.
systune uses a state-of-the-art nonsmooth optimizer to tune the controller parameters [1,2]. As opposed to “brute-force” optimization methods that rely on extensive simulation of the Simulink model, systune formulates and solves the tuning problem in the frequency domain. As a result, systune delivers high performance with most systems being tuned in seconds. Additionally, as the helicopter flight control system example demonstrates, systune does not require a good initial design and can be started from arbitrary, even unstable settings of the tuned parameters.
Published 2014 - 92155v00
References
-
P. Apkarian and D. Noll, "Nonsmooth H-infinity Synthesis," IEEE Transactions on Automatic Control, 51, pp. 71-86, 2006.
-
P. Apkarian and D. Noll, "Nonsmooth Optimization for Multiband Frequency-Domain Control Design," Automatica, 43, pp. 724-731, 2007.