designAuditoryFilterBank
Design auditory filter bank
Syntax
Description
filterBank = designAuditoryFilterBank(fs)filterBank.
filterBank = designAuditoryFilterBank(fs,Name=Value)
[
returns the center frequency and bandwidth of each filter in the filter bank. You can use
this output syntax with any of the previous input syntaxes.filterBank,Fc,BW] = designAuditoryFilterBank(___)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
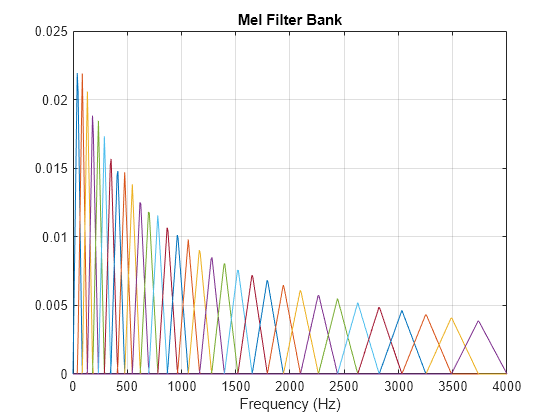
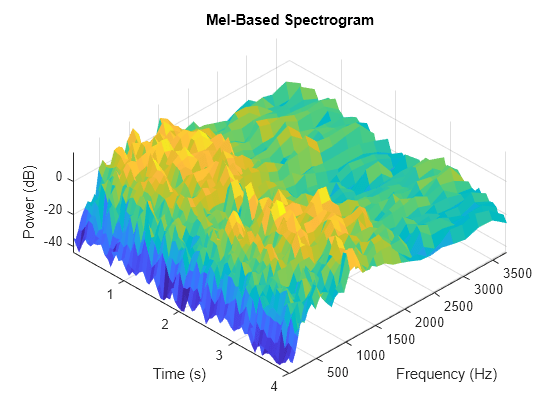
The mel filter bank is designed as half-overlapped triangles equally spaced on the mel scale. The mel scale can be in the O'Shaughnessy style, which follows [1], or the Slaney style, which follows [5].
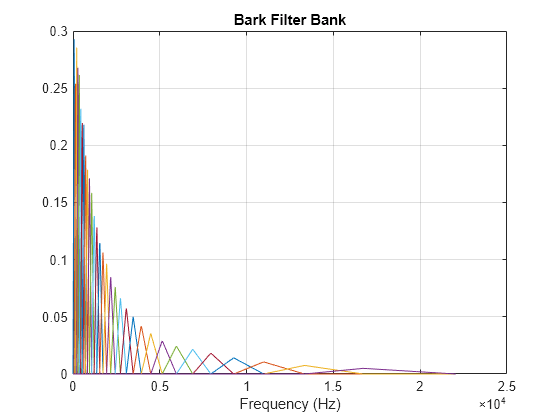
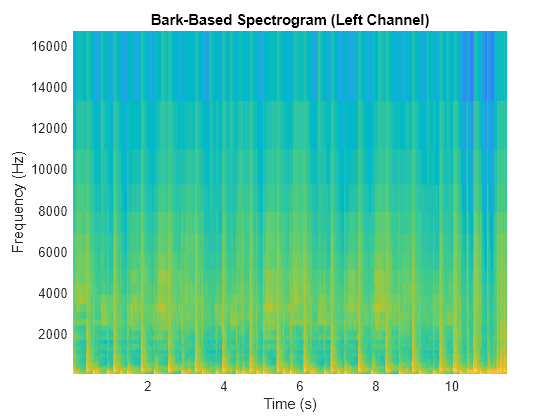
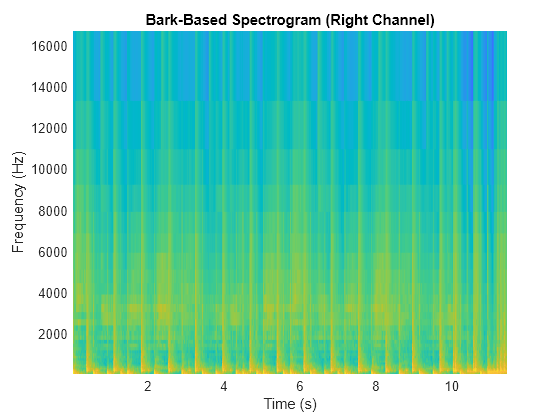
The Bark filter bank is designed as half-overlapped triangles equally spaced on the Bark scale. [2]
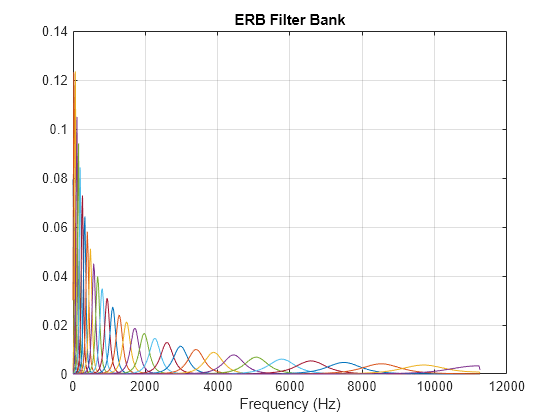
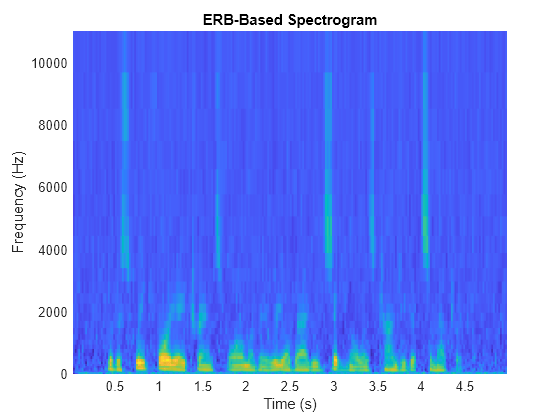
The ERB filter bank is designed as gammatone filters [4] whose center frequencies are equally spaced on the ERB scale. [3]
References
[1] O'Shaughnessy, Douglas. Speech Communication: Human and Machine. Reading, MA: Addison-Wesley Publishing Company, 1987.
[2] Traunmüller, Hartmut. "Analytical Expressions for the Tonotopic Sensory Scale." Journal of the Acoustical Society of America. Vol. 88, Issue 1, 1990, pp. 97–100.
[3] Glasberg, Brian R., and Brian C. J. Moore. "Derivation of Auditory Filter Shapes from Notched-Noise Data." Hearing Research. Vol. 47, Issues 1–2, 1990, pp. 103–138.
[4] Slaney, Malcolm. "An Efficient Implementation of the Patterson-Holdsworth Auditory Filter Bank." Apple Computer Technical Report 35, 1993.
[5] Slaney, Malcolm. "Auditory Toolbox: A MATLAB Toolbox for Auditory Modeling Work." Technical Report, Version 2, Interval Research Corporation, 1998.
Extended Capabilities
Version History
Introduced in R2019bSee Also
gammatoneFilterBank | melSpectrogram | hz2mel | hz2bark | hz2erb | erb2hz | bark2hz | mel2hz