imdct
Inverse modified discrete cosine transform
Description
X = imdct(Y,win,Name,Value)Name to the specified Value.
Unspecified properties have default values.
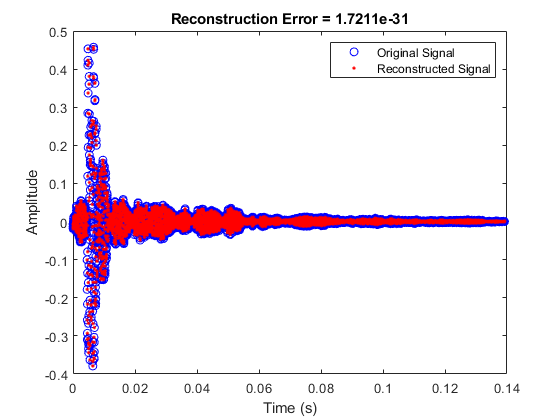
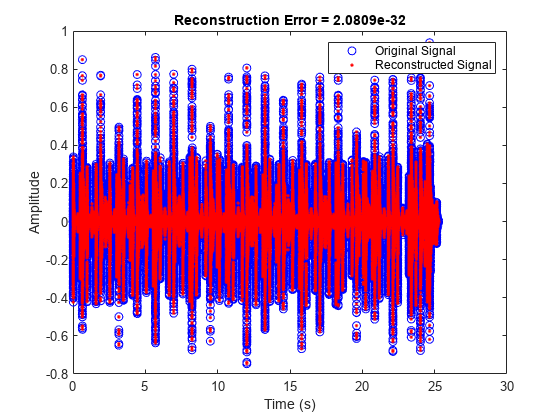
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
The inverse modified discrete cosine transform is a time-frequency transform. Given a
frequency domain input signal Y and window win, the
imdct function performs the follows steps for each independent channel:
Each frame of the input is converted into a time-domain representation:
where N is the number of elements in
win.Each frame of the time-domain signal is multiplied by the window,
win.The frames are overlap-added with 50% overlap to construct a contiguous time-domain signal. If
PadInputis set to true, theimdctfunction assumes the original input signal in the forward transform (mdct) was padded with N/2 zeros on the front and back and removes the padding. By default,PadInputis set totrue.
References
[1] Princen, J., A. Johnson, and A. Bradley. "Subband/Transform Coding Using Filter Bank Designs Based on Time Domain Aliasing Cancellation." IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP). 1987, pp. 2161–2164.
[2] Princen, J., and A. Bradley. "Analysis/Synthesis Filter Bank Design Based on Time Domain Aliasing Cancellation." IEEE Transactions on Acoustics, Speech, and Signal Processing. Vol. 34, Issue 5, 1986, pp. 1153–1161.
Extended Capabilities
Version History
Introduced in R2019a