Reverberator
Add reverberation to audio signal
Libraries:
Audio Toolbox /
Effects
Description
The Reverberator block adds reverberation to mono or stereo audio signals. You can tune parameters of the Reverberator block to mimic different acoustic environments.
Examples
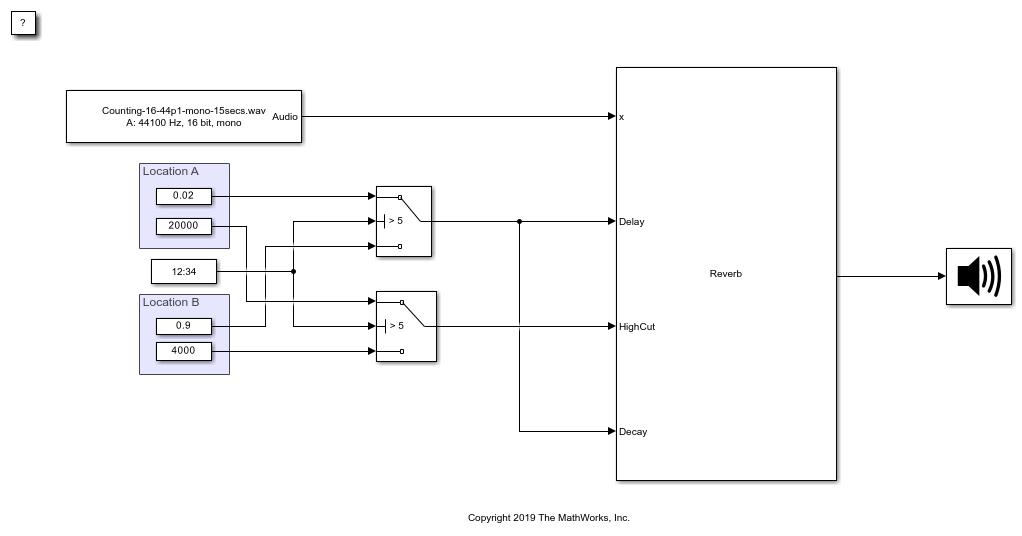
Mimic Acoustic Environments
Examine the Reverberator block in a Simulink® model and tune parameters. The reverberation parameters in this model mimic a large room with hard walls, such as a gymnasium.
Trigger Reverberation Parameters
Examine the Reverberator block in a Simulink® model where the reverberation parameters are triggered by time.
Ports
Input
Matrix input –– Each column of the input is treated as an independent channel.
1-D vector input –– The input is treated as a single channel.
This port is unnamed unless you specify additional input ports.
Data Types: single | double
Dependencies
To enable this port, select Specify from input port for the Pre-delay (s) parameter.
Data Types: single | double
Dependencies
To enable this port, select Specify from input port for the Highcut frequency (Hz) parameter.
Data Types: single | double
Dependencies
To enable this port, select Specify from input port for the Diffusion parameter.
Data Types: single | double
Dependencies
To enable this port, select Specify from input port for the Decay factor parameter.
Data Types: single | double
Dependencies
To enable this port, select Specify from input port for the High frequency damping parameter.
Data Types: single | double
Dependencies
To enable this port, select Specify from input port for the Wet/dry mix parameter.
Data Types: single | double
Output
The Reverberator block outputs the reverberated signal as a two-column matrix.
Data Types: single | double
Parameters
If a parameter is listed as tunable, then you can change its value during simulation.
Pre-delay for reverberation is the time between hearing direct sound and the first early reflection. The value of Pre-delay (s) is proportional to the size of the room being modeled.
To specify Pre-delay (s) from an input port, select Specify from input port for the parameter.
Tunable: Yes
Lowpass filter cutoff is the –3 dB cutoff frequency for the single-pole lowpass filter at the front of the reverberator structure. It prevents the application of reverberation to high-frequency components of the input.
To specify Highcut frequency (Hz) from an input port, select Specify from input port for the parameter.
Tunable: Yes
Diffusion is proportional to the rate at which the reverb tail builds in density. Increasing Diffusion pushes the reflections closer together, thickening the sound. Reducing Diffusion creates more discrete echoes.
To specify Diffusion from an input port, select Specify from input port for the parameter.
Tunable: Yes
Decay factor is inversely proportional to the time it takes for reflections to run out of energy. To model a large room, use a long reverb tail (low decay factor). To model a small room, use a short reverb tail (high decay factor).
To specify Decay factor from an input port, select Specify from input port for the parameter.
Tunable: Yes
High frequency damping is proportional to the attenuation of high frequencies in the reverberation output. Setting High frequency damping to a large value makes high-frequency reflections decay faster than low-frequency reflections.
To specify High frequency damping from an input port, select Specify from input port for the parameter.
Tunable: Yes
Wet/dry mix is the ratio of wet (reverberated) signal to dry (original) signal that your Reverberator block outputs.
To specify Wet/dry mix from an input port, select Specify from input port for the parameter.
Tunable: Yes
When you select this parameter, the block inherits its sample rate from the input signal. When you clear this parameter, you specify the sample rate in Input sample rate (Hz).
Tunable: Yes
Dependencies
To enable this parameter, clear the Inherit sample rate from input parameter.
Interpreted execution– Simulate the model using the MATLAB® interpreter. This option reduces startup time and the simulation speed is comparable toCode generation. In this mode, you can debug the source code of the block.Code generation– Simulate the model using generated C code. The first time you run a simulation, Simulink® generates C code for the block. The C code is reused for subsequent simulations, as long as the model does not change. This option requires additional startup time, but the speed of the subsequent simulations is comparable toInterpreted execution.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Algorithms
The algorithm to add reverberation follows the plate-class reverberation topology described in [1] and is based on a 29,761 Hz sample rate.
The algorithm has five stages.

The description for the algorithm that follows is for a stereo input. A mono input is a simplified case.
A stereo signal is converted to a mono signal: .
A delay followed by a lowpass filter preconditions the mono signal.

The pre-delay output is determined as , where the Pre-delay (s) parameter determines the value of k.
The signal is fed through a single-pole lowpass filter with transfer function
where
fc is the cutoff frequency specified by the Pre-delay (s) parameter.
fs is the sampling frequency specified by the Inherit sample rate from input parameter or the Input sample rate (Hz) parameter.
The signal is decorrelated by passing through a series of four allpass filters.

The allpass filters are of the form
where β is the coefficient specified
by the Diffusion property and k is
the delay as follows:
For AP1, k =
142.For AP2, k =
107.For AP3, k =
379.For AP4, k =
277.
The signal is fed into the tank, where it circulates to simulate the decay of a reverberation tail.

The following description tracks the signal as it progresses through the top of the tank. The signal progression through the bottom of the tank follows the same pattern, with different delay specifications.
The new signal enters the top of the tank and is added to the circulated signal from the bottom of the tank.
The signal passes through a modulated allpass filter:
β is the coefficient specified by the Diffusion parameter.
k is the variable delay specified by a 1 Hz sinusoid with amplitude = (8/29761) × (sample rate). To account for fractional delay resulting from the modulating k, allpass interpolation is used [2].
The signal is delayed again, and then passes through a lowpass filter:
φ is the coefficient specified by the High frequency damping parameter.
The signal is multiplied by a gain specified by the Decay factor parameter. The signal then passes through an allpass filter:
β is the coefficient specified by the Diffusion parameter.
k is set to
1800for the top of the tank and2656for the bottom of the tank.
The signal is delayed again and then circulated to the bottom half of the tank for the next iteration.
A similar pattern is executed in parallel for the bottom half
of the tank. The output of the tank is calculated as the signed sum
of delay lines picked off at various points from the tank. The summed
output is multiplied by 0.6.
The wet (processed) signal is then added to the dry (original) signal:
where the Wet/dry mix parameter determines κ.
References
[1] Dattorro, Jon. "Effect Design, Part 1: Reverberator and Other Filters." Journal of the Audio Engineering Society. Vol. 45, Issue 9, 1997, pp. 660–684.
[2] Dattorro, Jon. "Effect Design, Part 2: Delay-Line Modulation and Chorus." Journal of the Audio Engineering Society. Vol. 45, Issue 10, 1997, pp. 764–788.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2016a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleziona un sito web
Seleziona un sito web per visualizzare contenuto tradotto dove disponibile e vedere eventi e offerte locali. In base alla tua area geografica, ti consigliamo di selezionare: .
Puoi anche selezionare un sito web dal seguente elenco:
Come ottenere le migliori prestazioni del sito
Per ottenere le migliori prestazioni del sito, seleziona il sito cinese (in cinese o in inglese). I siti MathWorks per gli altri paesi non sono ottimizzati per essere visitati dalla tua area geografica.
Americhe
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)