Progettazione di un servo controller LQR in Simulink

Questo esempio mostra la progettazione di un servo controller LQR in Simulink® utilizzando un'applicazione per l'autopilota di un aereo.

Aprire il modello di aereo.

open_system("lqrpilot")

In questo modello:

• Il blocco Linearized Dynamics contiene la cellula linearizzata.

• sf_aerodyn è un blocco di funzione S contenente le equazioni non lineari per $\left(\theta ,\varphi \right)=\left(0,{15}^{\circ }\right)$.

• Il segnale di errore tra $\varphi$ e ${\varphi }_{\mathrm{ref}}$ viene fatto passare per un integratore che contribuisce ad azzerare l'errore.

L'apertura del modello carica inoltre il file MAT lqrpilotData che contiene i seguenti dati.

• Le matrici A e B delle equazioni di stato

• La matrice di stato A15 linearizzata

• La matrice K_lqr del guadagno LQG finale

Equazioni stato-spazio dell'aeromobile

Questa equazione è l'equazione di stato standard di un sistema stato-spazio.

$$\dot{\mathit{x}}=\mathit{A}\mathit{x}+\mathit{B}\mathit{u}$$

Per il sistema dell'aeromobile, il vettore di stato è il seguente.

$$\mathit{x}={\left[\mathit{u},\mathit{v},\mathit{w},\mathit{p},\mathit{q},\mathit{r},\theta ,\varphi \right]}^{\mathit{T}}$$

Le variabili $\mathit{u}$, $\mathit{v}$ e $\mathit{w}$ sono le tre velocità rispetto al telaio del corpo, come mostrato nella figura seguente.

Le variabili $\varphi$ e $\theta$ sono il rollio e il beccheggio. $\mathit{p}$, $\mathit{q}$ e $\mathit{r}$ sono rispettivamente il rollio, il beccheggio e i tassi d’imbardata.

Le dinamiche dell’aeromobile sono non lineari. La seguente equazione mostra i componenti non lineari aggiunti all'equazione stato-spazio, dove $\mathit{g}$ è l'accelerazione dovuta alla gravità.

$$\dot{\mathit{x}}=\mathit{Ax}+\mathit{Bu}+\left[\begin{array}{c}-\mathit{g}\cdot \sin \theta \\ \mathit{g}\cdot \cos \theta \cdot \sin \varphi \\ \mathit{g}\cdot \cos \theta \cdot \cos \varphi \\ 0\\ 0\\ 0\\ \mathit{q}\cdot \cos \varphi -\mathit{r}\cdot \sin \varphi \\ \left(\mathit{q}\cdot \sin \varphi +\mathit{r}\cdot \cos \varphi \right)\cdot \tan \theta \end{array}\right]$$

Trimming

Ai fini della progettazione LQG, le dinamiche non lineari sono sottoposte a trimming a $\varphi ={15}^{\circ }$ e le variabili $\mathit{p}$, $\mathit{q}$, $\mathit{r}$ e $\theta$ sono impostate a zero. Dato che $\mathit{u}$, $\mathit{v}$ e $\mathit{w}$ non influiscono sul termine non lineare dell'equazione precedente, il risultato è un modello linearizzato intorno a $\left(\theta ,\varphi \right)=\left(0,{15}^{\circ }\right)$, con tutti i restanti stati impostati a zero.

Lo script lqrdes mostra come calcolare il modello linearizzato A15 in questo punto di funzionamento sottoposto a trimming.

Definizione del problema

L’obiettivo della progettazione è di eseguire una virata coordinata e costante, come illustrato in questa figura.

Per raggiungere questo obiettivo è necessario progettare un controller che comandi una virata costante tramite l’esecuzione di un rollio di 60°. Si assuma inoltre che l'angolo di beccheggio $\theta$ debba rimanere il più vicino possibile a zero.

Risultati

Lo script lqrdes mostra come calcolare la matrice K_lqr del guadagno LQG.

Nel modello lqrpilot, assicurarsi che il blocco switch sia configurato per selezionare l'output del blocco Nonlinear Dynamics.

Eseguire il modello.

sim("lqrpilot")

Visualizzare la risposta del rollio $\varphi$ a una variazione di gradino di 60°. Il sistema traccia il rollio comandato in circa 60 secondi.

open_system("lqrpilot/phi (roll angle)")

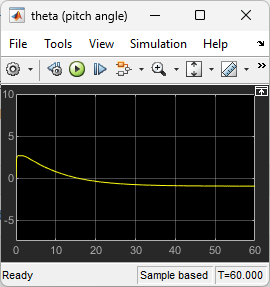
Visualizzare l'angolo di beccheggio $\theta$. Il controller è riuscito a mantenere l'angolo di beccheggio a un valore relativamente basso.

open_system("lqrpilot/theta (pitch angle)")

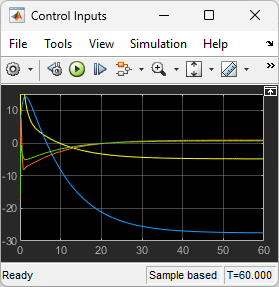
Infine, visualizzare gli input di controllo.

open_system("lqrpilot/Control Inputs")

È possibile regolare i valori Q e R nello script lqrdes per provare diversi potenziali progetti. È inoltre possibile confrontare le simulazioni della dinamica del sistema lineare e non lineare per vedere gli effetti delle non linearità sulle prestazioni del sistema.

Vedi anche

Argomenti

• Filtri di Kalman
• Progettazione di un controllo lineare-quadratico-gaussiano (LQG)
• Progettazione di un regolatore LQG
• Progettazione di un servo controller LQG