Rimozione del rumore a bassa frequenza in Simulink utilizzando un filtro adattivo LMS normalizzato

La traduzione di questa pagina non è aggiornata. Fai clic qui per vedere l'ultima versione in inglese.

I filtri adattivi tengono traccia della natura dinamica di un sistema, consentendo di eliminare i segnali che variano nel tempo. Le librerie DSP System Toolbox™ contengono blocchi che implementano algoritmi di filtro adattivo del minimo quadratico medio (LMS), LMS a blocchi, LMS a blocchi rapidi e del minimo quadratico ricorsivo (RLS). Questi filtri minimizzano la differenza tra il segnale in uscita e il segnale desiderato, alterando i loro coefficienti del filtro. Nel tempo, il segnale di uscita del filtro adattivo si avvicina maggiormente al segnale che si desidera riprodurre.

Progettazione di un filtro adattivo in Simulink

Questo esempio utilizza:

Apri live script

Questo esempio riguarda la progettazione di un filtro adattivo LMS per rimuovere il rumore a bassa frequenza del segnale:

Se il modello creato in Aggiunta di un filtro digitale al modello non è aperto sul desktop, aprire ex_gstut5 che è un modello equivalente.

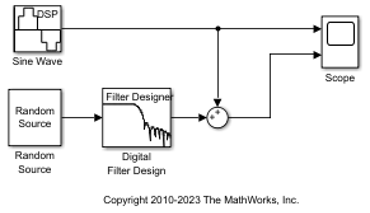
Aprire la libreria DSP System Toolbox™ digitando dsplib nel prompt dei comandi di MATLAB®.

Rimuovere il rumore a bassa frequenza dal segnale aggiungendo un blocco LMS Filter al sistema. Nello scenario dell’areo, questo equivale a sottrarre il rumore del vento all’interno della cabina di pilotaggio dall’ingresso del microfono. Fare doppio clic sulla libreria Filtering, quindi fare doppio clic sulla sotto libreria Adaptive Filters. Aggiungere il blocco LMS Filter nel modello.

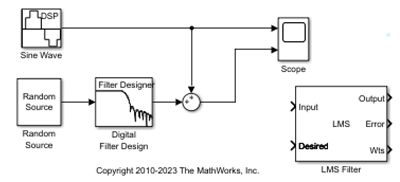
Impostare i parametri del blocco LMS Filter per modellare l'output del blocco Digital Filter Design. Aprire la finestra di dialogo del blocco LMS Filter facendo doppio clic sul blocco stesso. Impostare e applicare i parametri del blocco come segue:

Algoritmo = Normalized LMS
Lunghezza del filtro = 32
Specificare la dimensione del passo tramite = Dialog
Dimensione del passo (mu) = 0,1
Fattore di dispersione (0 to 1) = 1,0
Valore iniziale dei pesi del filtro = 0
Azzerare la casella di spunta Adapt port (Adatta porta).
Ripristinare la porta = None
Selezionare la casella di spunta Output filter weights (Pesi del filtro in uscita).

Sulla base di questi parametri, il blocco LMS Filter calcola i pesi del filtro utilizzando le equazioni LMS normalizzate. L'ordine del filtro specificato è lo stesso dell'ordine del filtro del blocco Digital Filter Design. Il parametro Step size (mu) (Dimensione del passo (mu)) definisce la granularità delle fasi di aggiornamento del filtro. Poiché il parametro Leakage factor (0 to 1) (Fattore di dispersione (da 0 a 1)) è impostato su 1,0, i valori attuali del coefficiente del filtro dipendono dalle condizioni iniziali del filtro e da tutti i valori precedenti in entrata. Il valore iniziale dei pesi del filtro (coefficienti) è zero. Poiché è stata selezionata la casella di spunta Output filter weights (Pesi del filtro in uscita), la porta Wts viene visualizzata sul blocco. Il blocco fornisce i pesi del filtro da questa porta.

Ora che i parametri di blocco del blocco LMS Filter sono stati impostati, si può incorporare questo blocco nel diagramma a blocchi.

Aggiunta di un filtro adattivo al modello

Questo esempio utilizza:

Apri live script

In questo esempio, il segnale sinusoidale originale viene recuperato incorporando nel sistema il filtro adattivo progettato in Progettazione di un filtro adattivo in Simulink. Nello scenario dell’aereo, il filtro adattivo modella il rumore a bassa frequenza sentito all'interno della cabina di pilotaggio. Di conseguenza, è possibile rimuovere il rumore in modo che la voce del pilota sia l'unico input per il microfono:

Se il modello creato in Progettazione di un filtro adattivo in Simulink non è aperto sul desktop, aprire ex_gstut6 che è un modello equivalente.

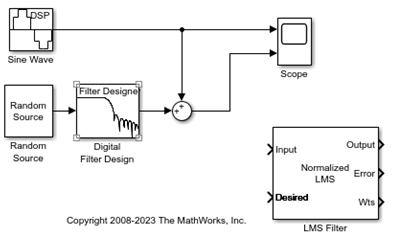
Aggiungere un blocco Sum al modello per sottrarre l'uscita del filtro adattivo dal segnale sinusoidale con rumore a bassa frequenza. Dalla libreria Simulink fallback for tm_simulink Math Operations, trascinare un blocco Sum nel modello. Aprire la finestra di dialogo del blocco Sum facendo doppio clic sul blocco stesso. Modificare il parametro List of signs (Elenco dei segni) in |+-, quindi fare clic su OK.

Incorporare il blocco LMS Filter nel sistema.

Collegare l'uscita del blocco Random Source alla porta in ingresso del blocco LMS Filter. Nello scenario dell’aereo, il rumore casuale è il rumore bianco misurato dal sensore all'esterno dell’aereo. Il blocco LMS Filter modella l'effetto della fusoliera dell'aeroplano sul rumore.
Collegare l'uscita del blocco Digital Filter Design alla porta desiderata sul blocco LMS Filter. Questo è il segnale che si desidera riprodurre dal blocco LMS.
Collegare l'uscita del blocco LMS Filter alla porta negativa del blocco Sum aggiunto nel passaggio 2.
Collegare l'uscita del primo blocco Sum alla porta positiva del secondo blocco Sum. Il modello dovrebbe ora essere simile alla figura seguente.

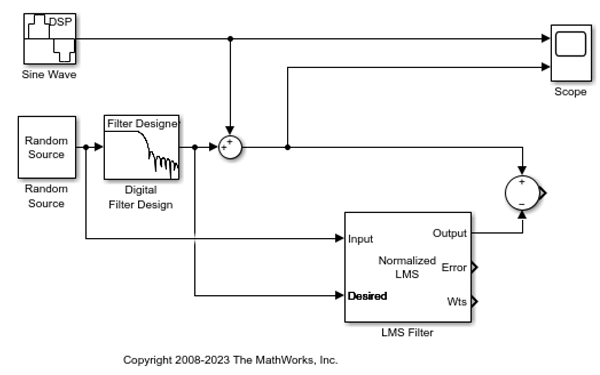
L'ingresso positivo al secondo blocco Sum è la somma del segnale in entrata e del rumore a bassa frequenza s(n) + y. L'ingresso negativo al secondo blocco Sum è la miglior stima del blocco LMS Filter del rumore a bassa frequenza y'. Quando si sottraggono i due segnali, si ottiene un'approssimazione del segnale in entrata.

${s (n)}_{approx} = s (n) + y - y^{'}$

In questa equazione:

$s (n)$ è il segnale in entrata.
${s (n)}_{approx}$ è l’approssimazione del segnale in entrata.
$y$ è il rumore creato dal blocco Random Source e dal blocco Digital Filter Design.
$y^{'}$ è l'approssimazione del rumore del blocco LMS Filter.

Poiché il blocco LMS Filter può solo approssimare il rumore, è ancora presente una differenza tra il segnale in entrata e la sua approssimazione. Nei passaggi successivi, impostare il blocco Scope in modo da poter confrontare il segnale sinusoidale originale con la sua approssimazione.

Aggiungere due ulteriori ingressi e assi al blocco Scope. Aprire la finestra di dialogo del blocco Scope facendo doppio clic sul blocco stesso. Fare clic sul pulsante Parameters (Parametri). Per il parametro Number of axes (Numero di assi), immettere 4. Chiudere la finestra di dialogo facendo clic su OK.

Etichettare i nuovi assi Scope. Nella finestra Scope, fare clic con il pulsante destro del mouse sul terzo asse e selezionare Axes properties (Proprietà dell’asse). Proprietà Scope: si apre la finestra di dialogo dell’asse 3. Nella casella Title (Titolo), immettere Approximation of Input Signal. Chiudere la finestra di dialogo facendo clic su OK. Ripetere questa procedura per il quarto asse ed etichettarlo Error.

Collegare l'uscita del secondo blocco Sum alla terza porta del blocco Scope.

Collegare l'uscita della porta Error (Errore) sul blocco LMS Filter alla quarta porta del blocco Scope. Il modello dovrebbe ora essere simile alla figura seguente.

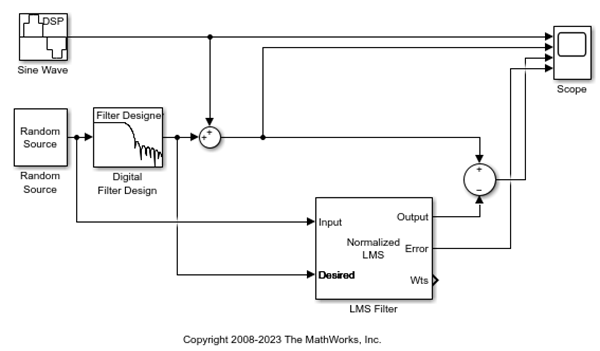
In questo esempio, l'uscita della porta Error (Errore) è la differenza tra il segnale desiderato del filtro LMS e il suo segnale in uscita. Poiché l'errore non è mai zero, il filtro continua a modificare i coefficienti del filtro per approssimare meglio il rumore a bassa frequenza. Migliore è l'approssimazione, maggiore è il rumore a bassa frequenza che può essere rimosso dal segnale sinusoidale. Il prossimo argomento Visualizzazione dei coefficienti del filtro adattivo, illustra come visualizzare i coefficienti del filtro adattivo man mano che cambiano nel tempo.

Visualizzazione dei coefficienti del filtro adattivo

Questo esempio utilizza:

Apri live script

I coefficienti di un filtro adattativo cambiano nel tempo secondo un algoritmo scelto. Una volta che l'algoritmo ottimizza la prestazione del filtro, questi coefficienti di filtro raggiungono i loro valori di stato stazionario. Mentre la simulazione è in esecuzione, è possibile visualizzare la variazione dei coefficienti per osservare il loro stabilizzarsi sui valori di stato stazionario. Quindi, si può determinare se questi valori sono implementabili nel sistema corrente:

Se il modello creato in Add an Aggiunta di un filtro adattivo al modello (Aggiungi un) non è aperto sul desktop, aprire ex_gstut7 che è un modello equivalente.

Si noti che la porta Wts del filtro adattivo, che produce i pesi del filtro, deve ancora essere collegata.

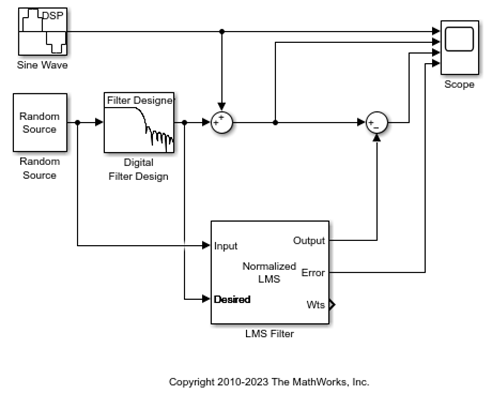
Aprire la libreria DSP System Toolbox™ digitando dsplib nel prompt dei comandi di MATLAB®.

Visualizzare i coefficienti del filtro collegando un blocco Time Scope alla porta Wts del blocco LMS Filter.

Modificare le seguenti proprietà di configurazione nel blocco Time Scope:

Arco di tempo = 0,05
Limiti Y (minimo) = -0,15
Limiti Y (massimo) = 0,5

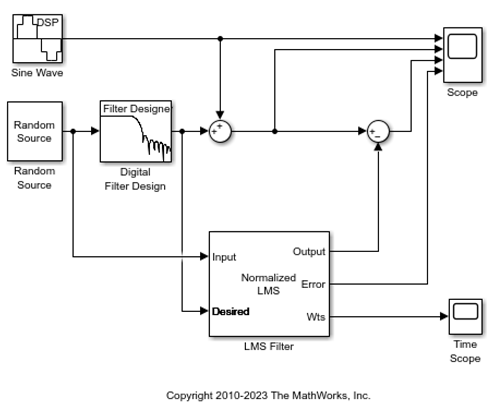
Aprire Model Settings (Impostazioni modello). Nella scheda Modeling (Modellazione), fare clic su Model Settings (Impostazioni modello). Nel pannello Solver (Risolutore), impostare i seguenti parametri di configurazione:

Tempo di arresto = inf
Tipo = Fixed-step
Solver = discrete (no continuous states)

Consigliamo questi parametri di configurazione per i modelli che contengono blocchi DSP System Toolbox. Poiché questi blocchi calcolano i valori direttamente anziché risolvere equazioni differenziali, è necessario configurare Simulink® Solver affinché si comporti come uno schedulatore. Quando il Solver è in modalità di schedulazione, utilizza il tempo di campionamento di un blocco per determinare quando viene eseguito il codice dietro ogni blocco. Ad esempio, il tempo di campionamento dei blocchi Sine Wave e Random Source in questo modello è 0,05. Il Solver esegue il codice dietro questi blocchi e dietro ogni altro blocco con questo tempo di campionamento, una volta ogni 0,05 secondi.

Nota: quando si lavora con modelli che contengono blocchi DSP System Toolbox, utilizzare i blocchi di origine che consentono di specificare il loro tempo di campionamento. Se il blocco di origine non dispone di un parametro Sample time (Tempo di campionamento), è necessario aggiungere un blocco di mantenimento dell'ordine zero nel modello e utilizzarlo per specificare il tempo di campionamento. Per ulteriori informazioni, vedere Continuous-Time Source Blocks. L'eccezione a questa regola è il blocco Constant, che può avere un tempo di campionamento costante. Quando questo blocco è presente, Simulink lo esegue e registra il valore costante una volta, all'inizio della simulazione, e successivamente ogni volta che si sintonizza un parametro. Ciò consente simulazioni più veloci e un codice generato più compatto.

Eseguire il modello e osservare il comportamento dei coefficienti del filtro nel Time Scope che si apre automaticamente all'avvio della simulazione. Nel tempo, i coefficienti del filtro si avvicinano ai loro valori di stato stazionario.

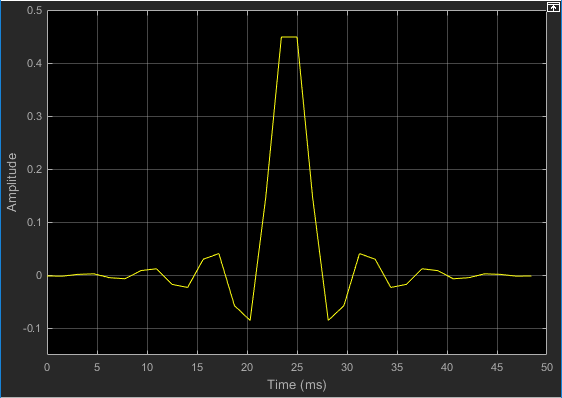
È inoltre possibile visualizzare il comportamento del sistema nella finestra Scope. Nel tempo, l'errore diminuisce e l'approssimazione del segnale in entrata corrisponde maggiormente al segnale di ingresso sinusoidale originale.

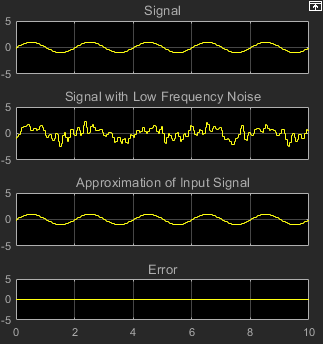
È stato creato un modello in grado di cancellare il rumore adattivo.

Sommario

Si è appreso come creare un filtro passa bassa utilizzando il blocco Digital Filter Design. Si è inoltre appreso come creare un filtro adattivo utilizzando il blocco LMS Filter. Il prodotto DSP System Toolbox dispone di altri blocchi in grado di progettare e implementare filtri digitali e adattivi. Per ulteriori informazioni sulle capacità di filtraggio di questo prodotto, vedere Filter Design e Filter Analysis.

Poiché tutti i blocchi in questo modello hanno lo stesso tempo di campionamento, questo modello è a frequenza singola e Simulink^® lo ha eseguito in modalità Solver SingleTasking. Se i blocchi nel modello hanno tempi di campionamento diversi, il modello è a multifrequenza e Simulink potrebbe eseguirlo in modalità Solver MultiTasking. Per ulteriori informazioni sulle modalità solver, vedere Recommended Settings for Discrete-Time Simulations.

Per informazioni su come generare codice dal modello utilizzando il prodotto Simulink Coder™, vedere Generate C Code from Simulink Model.

Vedi anche

LMS Filter | Digital Filter Design