Code Generation of Matrices and Arrays
MATLAB® stores matrix data and arrays (1–D, 2–D, ...) in column-major format as a vector. Simulink® and the code generator can store array data in column-major or row-major format. For an array stored in column-major layout, the elements of the columns are contiguous in memory. In row-major layout, the elements of the rows are contiguous. Array layout is also referred to as order, format, and representation. The order in which elements are stored can be important for integration, usability, and performance. Certain algorithms perform better on data stored in a particular order.
Programming languages and environments assume a single array layout for all data. MATLAB and Fortran use column-major layout by default, whereas C and C++ use row-major layout. With Simulink Coder™, you can generate C/C++ code that uses row-major layout or column-major layout.
Array Storage in Computer Memory
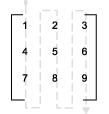
Computer memory stores data in terms of one-dimensional arrays. For example, when you declare a 3-by-3 matrix, the software stores this matrix as a one-dimensional array with nine elements. By default, MATLAB stores these elements with a column-major array layout. The elements of each column are contiguous in memory.
Consider the matrix
A:
A =
1 2 3
4 5 6
7 8 9A translates to an array of length 9 in
this order: A(1) = A(1,1) = 1; A(2) = A(2,1) = 4; A(3) = A(3,1) = 7; A(4) = A(1,2) = 2; A(5) = A(2,2) = 5;
In column-major format, the next element of an array in memory is accessed by incrementing the first index of the array. For example, these element pairs are stored sequentially in memory:
A(i)andA(i+1)B(i,j)andB(i+1,j)C(i,j,k)andC(i+1,j,k)
The matrix A is represented in memory by default with this
arrangement:
1 4 7 2 5 8 3 6 9
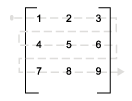
In row-major array layout, the programming language stores row elements contiguously in memory. In row-major layout, the elements of the array are stored as:
1 2 3 4 5 6 7 8 9
You can store the N-dimensional arrays in column-major or row-major layout. In column-major layout, the elements from the first (leftmost) dimension or index are contiguous in memory. In row-major layout, the elements from the last (rightmost) dimension or index are contiguous.
For more information on the internal representation of MATLAB data, see MATLAB Data.
Code generation software uses column-major format by default for several reasons:
The world of signal and array processing is largely in column-major array layout: MATLAB, LAPack, Fortran90, and DSP libraries.
A column is equivalent to a channel in frame-based processing. In this case, column-major storage is more efficient.
A column-major array is self-consistent with its component submatrices:
A column-major 2-D array is a simple concatenation of 1-D arrays.
A column-major 3-D array is a simple concatenation of 2-D arrays.
The stride is the number of memory locations to index to the next element in the same dimension. The stride of the first dimension is one element. The stride of the nth dimension element is the product of the sizes of the lower dimensions.
Row-major n-D arrays have their stride of 1 for the highest dimension. Submatrix manipulations are typically accessing a scattered data set in memory, which does not allow for efficient indexing.
C uses row-major format. MATLAB and Simulink use column-major format by default. You can configure the code generation software to generate code with a row-major array layout. If you are integrating external C code with the generated code, see the considerations listed in this table.
| Action | Consider |
|---|---|
| Configure array layout of the model for code generation. | In the Configuration Parameters dialog box, set model configuration parameter
Array layout to
Column-major or
Row-major. |
| Enable efficient row-major algorithms for simulation and code generation. | Select model configuration parameter Use algorithms optimized for row-major array layout. |
| Integrate external C code functions in row-major array layout with the generated code. | Create S-functions that integrate external code functions with the generated code by using:
Use the C Caller block to call external C functions into Simulink. Specify array layout of custom C functions by using model configuration parameter Default function array layout. You can also use |
Code Generator Matrix Parameters
The compiled model file, model.rtw.rtw file, paste it into a MATLAB file, and have MATLAB recognize it.
Column-Major Layout
For example, the 3-by-3 matrix in the Constant block
1 2 3
4 5 6
7 8 9model.rtwParameter {
Identifier "Constant_Value"
LogicalSrc P0
Protected no
Value [1.0, 4.0, 7.0, 2.0, 5.0, 8.0, 3.0, 6.0, 9.0]
CGTypeIdx 18
ContainerCGTypeIdx 19
ReferencedBy Matrix(1,4)
[[0, -1, 0, 0];]
GraphicalRef Matrix(1,2)
[[0, 1];]
BHMPrmIdx 0
GraphicalSource [0, 1]
OwnerSysIdx [0, -1]
VarGroupIdx [1, 0]
WasAccessedAsVariable 1
}The model_data.c
Parameters model_P = {
/* Expression: [ [1,2,3] ; [4,5,6] ;[7,8,9]]
* Referenced by: '<Root>/Constant '
*/
{ 1.0, 4.0, 7.0, 2.0, 5.0, 8.0, 3.0, 6.0, 9.0 }
};Row-Major Layout
For example, the 3-by-3 matrix in the Constant block
1 2 3
4 5 6
7 8 9model.rtwParameter {
Identifier "Constant_Value"
LogicalSrc P0
Protected no
Value [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0]
CGTypeIdx 18
ContainerCGTypeIdx 19
ReferencedBy Matrix(1,4)
[[0, -1, 0, 0];]
GraphicalRef Matrix(1,2)
[[0, 1];]
BHMPrmIdx 0
GraphicalSource [0, 1]
OwnerSysIdx [0, -1]
VarGroupIdx [1, 0]
WasAccessedAsVariable 1
}The model_data.h
Parameters model_P = {
/* Expression: [ [1,2,3] ; [4,5,6] ;[7,8,9]]
* Referenced by: '<Root>/Constant '
*/
{ 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0 }
};Internal Data Storage for Complex Number Arrays
Simulink and code generator internal data storage formatting differs from MATLAB internal data storage formatting only in the storage of complex number arrays. In MATLAB, the real and imaginary parts are stored in separate arrays. In Simulink and the code generator, the parts are stored in an interleaved format. The numbers in memory alternate real, imaginary, real, imaginary, and so forth. This convention allows efficient implementations of small signals on Simulink lines, for Mux blocks, and other virtual signal manipulation blocks. For example, the signals do not actively copy their inputs, just the references.
Unsupported Blocks for Row-Major Code Generation
The code generator does not support these blocks for code generation in row-major array layout.
Continuous
Action Port
Derivative
Integrator
Integrator Limited
Integrator, Second-Order
Integrator, Second-Order Limited
PID Controller
PID Controller (2DOF)
State-Space
Transfer Fcn
Transport Delay
Variable Time Delay
Variable Transport Delay
Zero-Pole
User-Defined Functions
Level-2 MATLAB S-Function
Sources
From Spreadsheet
Signal Attributes
IC
Discrete
The code generator does not support these blocks for code generation in row-major
array layout if the Input processing block parameter is set to
Elements as channels (sample based) and the block is
connected to a State Reader or State Writer block.
Discrete Transfer Function
Discrete Filter
Discrete FIR Filter
Additional Limitations for Row-Major Code Generation
Bounded variable-size signals are not supported for row-major code generation.
The Stateflow®
rising,falling, andcrossingoperators are not supported for row-major code generation.
Model Advisor Checks for Row-Major Code Generation
Array layout can be important for integration, usability, and performance. Programming languages and environments assume a single array layout for all data; you can generate C/C++ code that uses row-major layout. The code that you generate by using row-major algorithms performs with better speed and efficient memory usage when operating on data with row-major array layout.
To check that your model is configured for efficient row-major code generation and check the compatibility of existing elements with row-major code generation, use the Model Advisor checks in folder By Task > Row-Major Code Generation. Checks include: