PLL with Feed Forward

Compute position and angular frequency from orthogonal sinusoidal signals

Since R2023b

• 

Libraries:
Motor Control Blockset / Signal Management

Description

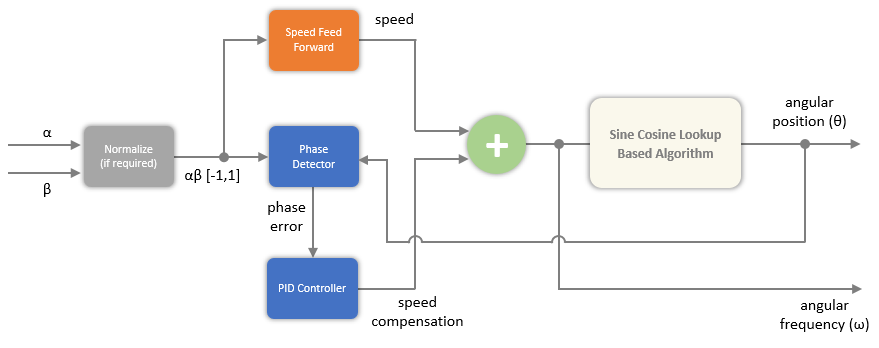
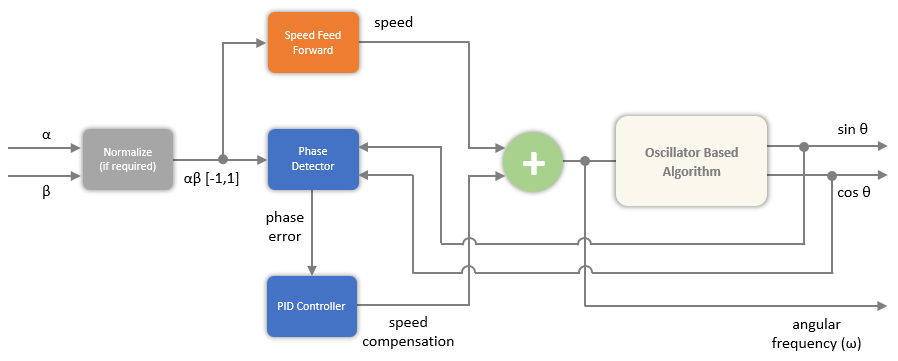
The PLL with Feed Forward block computes angular position (θ) or its sine and cosine equivalents (sin θ, cos θ) and the angular frequency (ω) from two orthogonal sinusoidal signals.

In addition to the angular frequency, the block uses either a sine-cosine lookup table to calculate the angular position or an oscillator based algorithm to compute the sine and cosine equivalents of position. You can use the Position output parameter to output either angular position or its sine and cosine equivalents.

The two orthogonal sinusoidal input signals must have identical peak magnitudes. If the inputs are not normalized in the range of [-1,1], select the Enable input normalization parameter.

The following image shows the relationship between block inputs and outputs:

For more information on the block algorithm, see Algorithm.

Note

The block does not support 16-bit fixed-point inputs.

Examples

Simulate Initial Position Estimation and Field-Weakening Control of IPMSM Using Pulsating High-Frequency Injection and Extended EMF Observer

Uses sensorless techniques such as pulsating high-frequency injection and extended EMF observer to estimate and track motor position to simulate interior permanent magnet synchronous motor (IPMSM) operation using field-weakening control (FWC).

Open Model

Ports

Input

α — α-axis signal

scalar

Input signal along the α-axis.

Data Types: single | double | fixed point

β — β-axis signal

scalar

Input signal along the β-axis.

Data Types: single | double | fixed point

Rst — External reset pulse

scalar

External pulse that resets the block.

Data Types: single | double | fixed point

Output

θ — Angular position

scalar

Angular position (in either degrees, radians, or per-unit) that the block computes from the orthogonal input signals.

Dependencies

To enable this port, set the Position output parameter to Angular position.

Data Types: single | double | fixed point

Sin θ — Sine of angular position

scalar

Sine equivalent of the computed angular position.

Dependencies

To enable this port, set the Position output parameter to Sine and Cosine Position.

Data Types: single | double | fixed point

Cos θ — Cos of angular position

scalar

Cosine equivalent of the computed angular position.

Dependencies

To enable this port, set the Position output parameter to Sine and Cosine Position.

Data Types: single | double | fixed point

ω — Angular frequency

scalar

Angular frequency (in either degrees/sec, radians/sec, or hertz) of the orthogonal input signals.

Data Types: single | double | fixed point

Parameters

Enable input normalization — Enable block to normalize inputs

on (default) | off

The block normalizes the α and β orthogonal input signals only if you select this parameter.

Position output — Type of position output

Angular position (default) | Sine and Cosine Position

Type of position output that the block should generate:

• Angular position — Select this option to use a sine-cosine lookup table to compute the angular position (θ).

• Sine and Cosine Position — Select this option to use an oscillator based algorithm to compute the sine and cosine equivalents (sin θ and cos θ) of the angular position.

Discrete step size (s) — Sample time after which block executes again

50e-6 (default) | scalar

The fixed time interval (in seconds) between consecutive instances of block execution.

PLL Parameters

Frequency ratio — Ratio of frequencies of output and input signals

1 (default) | scalar

The ratio of the frequency of the output signal to the frequency of the input signal of the block.

Maximum application frequency (Hz) — Maximum applicable input frequency

7500 (default) | scalar

Maximum possible frequency of the input signals (in hertz).

Cutoff frequency for output filter (Hz) — Cutoff frequency of lowpass filter

15 (default) | scalar

Cutoff frequency of the lowpass filter that the block uses to filter the estimated angular frequency (in hertz).

Number of data points for lookup table — Size of lookup table array

1024 (default) | scalar

Size of the lookup table array that the block provides to the Sine-Cosine Lookup block, which is used internally. This parameter accepts a value between 125 and 4095.

Dependencies

To enable this parameter, set Position output to Angular position.

Proportional (P) — Proportional controller gain

942.4778 (default) | scalar

Proportional gain (K_p) of the PID controller used by the block to compute the angular frequency.

Integral (I) — Integral controller gain

222066.099 (default) | scalar

Integral gain (K_i) of the PID controller used by the block to compute the angular frequency.

Click Compute default parameters to calculate an approximate proportional gain (K_p) and integral gain (K_i) and update these fields.

Datatypes

Position unit — Unit of position output

Degrees (default) | Radians | Per-unit

Unit of the position output.

Dependencies

To enable this parameter, set Position output to Angular position.

Position data type — Data type of position output

single (default) | double | fixed point

Data type of the position output.

Frequency unit — Unit of angular frequency output

Degrees/sec (default) | Radians/sec | Hz

Unit of the angular frequency output.

Frequency data type — Data type of angular frequency output

single (default) | double | fixed point

Data type of the angular frequency output.

Table data type — Data type of sine-cosine lookup table

single (default) | double | fixed point

Data type of the sine-cosine lookup table used by the block.

Dependencies

To enable this parameter, set Position output to Angular position.

Algorithms

The following image provides an overview of how the block uses an algorithm based on sine-cosine lookup table to compute the angular position (θ). Set the Position output to Angular position to use this algorithm.

The following image provides an overview of how the block uses an oscillator-based algorithm to compute the sine and cosine equivalents of angular position (θ). Set the Position output to Sine and Cosine Position to use this algorithm.

The following equation describes the state equation of the oscillator-based algorithm.

$$\dot{x}=\left[\begin{array}{cc}0& \omega \\ -\omega & 0\end{array}\right]x$$

where, ω is the frequency of oscillation.

Tuning feed-forward angular-frequency phase-locked loop (PLL)

The following image shows a linearized model of the angular frequency feed-forward PLL that you can use for tuning purposes.

From this model you can obtain the following transfer function of position estimation error (ΔE(s)) with respect to actual position (θ(s)) to tune the feed-forward PLL.

$$\frac{\Delta E\left(s\right)}{\theta \left(s\right)}=\frac{s^3}{\left(s+{\omega }_c\right)\left(s^2+K_{p}s+K_i\right)}$$

where:

• K_p and K_i are the proportional and integral gains, respectively, of the PID controller used by the block for angular frequency computation.

• ω_c is the cutoff frequency for the output filter.

References

[1] G. Liu, H. Zhang and X. Song, "Position-Estimation Deviation-Suppression Technology of PMSM Combining Phase Self-Compensation SMO and Feed-Forward PLL," in IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 9, no. 1, pp. 335-344, Feb. 2021, doi: 10.1109/JESTPE.2020.2967508.

[2] Se-Kyo Chung, "A phase tracking system for three phase utility interface inverters," in IEEE Transactions on Power Electronics, vol. 15, no. 3, pp. 431-438, May 2000, doi: 10.1109/63.844502.

[3] Sreeraman Rajan, Sichun Wang, Robert Inkol, and Alain Joyal. "Efficient Approximations for the Arctangent Function." IEEE SIGNAL PROCESSING MAGAZINE (MAY 2006).

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2023b