Lane Keeping Assist System
Simulate lane-keeping assistance using adaptive model predictive controller

Libraries:
Model Predictive Control Toolbox /
Automated Driving
Description
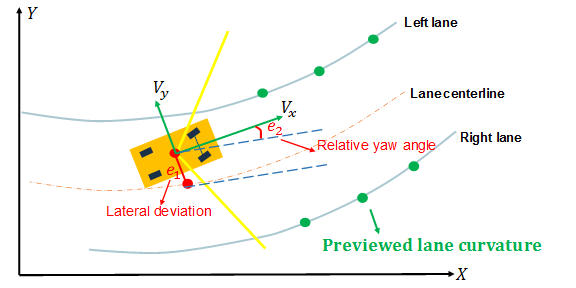
The Lane Keeping Assist System block simulates a lane keeping assist (LKA) system that keeps an ego vehicle traveling along the center of a straight or curved road by adjusting the front steering angle. The controller reduces the lateral deviation and relative yaw angle of the ego vehicle with respect to the lane centerline. The block computes optimal control actions while satisfying steering angle constraints using adaptive model predictive control (MPC).
To customize your controller, for example to use advanced MPC features or modify controller initial conditions, click Create LKA subsystem.
Examples
Lane Keeping Assist System Using Model Predictive Control
Design an MPC controller that keeps an ego vehicle traveling along the center of a straight or curved road by adjusting the front steering angle.
Lane Keeping Assist with Lane Detection
Simulate and generate code for an automotive lane keeping assist controller.
(Automated Driving Toolbox)
Ports
Input
Road curvature, specified as 1/R, where R is the radius of the curve in meters.
The road curvature is:
Positive when the road curves toward the positive Y axis of the global coordinate system.
Negative when the road curves toward the negative Y axis of the global coordinate system.
Zero for a straight road.
The controller models the road curvature as a measured disturbance with previewing. You can specify the curvature as a:
Scalar signal — Specify the curvature for the current control interval. The controller uses this curvature value across the prediction horizon.
Vector signal with length less than or equal to the Prediction Horizon parameter — Specify the current and predicted curvature values across the prediction horizon. If the length of the vector is less than the prediction horizon, then the controller uses the final curvature value in the vector for the remainder of the prediction horizon.
Ego vehicle velocity in m/s.
Ego vehicle lateral deviation in meters from the centerline of the lane. The lateral deviation e1 is positive when the ego vehicle is to the right of the centerline and negative when the ego vehicle is to the left of the centerline.
Ego vehicle longitudinal axis angle in radians from the centerline of the lane, defined as:
Here, θe is the ego vehicle angle and θc is the centerline angle, with both angles defined in the global coordinate frame.
Minimum front steering angle constraint in radians. Use this input port when the minimum steering angle varies at run time.
Dependencies
To enable this port, select corresponding Use external source parameter.
Maximum front steering angle constraint in radians. Use this input port when the maximum steering angle varies at run time.
Dependencies
To enable this port, select corresponding Use external source parameter.
Controller optimization enable signal. When this signal is:
Nonzero, the controller performs optimization calculations and generates a Steering angle control signal.
Zero, the controller does not perform optimization calculations. In this case, the Steering angle output signal remains at the value it had when the optimization was disabled. The controller continues to update its internal state estimates.
Dependencies
To enable this port, select the Use external signal to enable or disable optimization parameter.
Actual steering angle in radians applied to the ego vehicle. The controller uses this signal to estimate the ego vehicle model states. Use this input port when the control signal applied to the ego vehicle does not match the optimal control signal computed by the model predictive controller. This mismatch can occur when, for example:
The Lane Keeping Assist System is not the active controller. Maintaining an accurate state estimate when the controller is not active prevents bumps in the control signal when the controller becomes active.
The steering actuator fails and does not provide the correct control signal to the ego vehicle.
Dependencies
To enable this port, select the Use external control signal for bumpless transfer between PFC and other controllers parameter.
State matrix of ego vehicle predictive model. The number of rows in the state matrix corresponds to the number of states in the predictive model. This matrix must be square.
The ego vehicle predictive model defined by Vehicle dynamics matrix A, Vehicle dynamics matrix B, and Vehicle dynamics matrix C must be minimal.
Dependencies
To enable this port, select the Use vehicle model parameter.
Input-to-state matrix of ego vehicle predictive model. The number of rows in this signal must match the number of rows in Vehicle dynamics matrix A.
The ego vehicle predictive model defined by Vehicle dynamics matrix A, Vehicle dynamics matrix B, and Vehicle dynamics matrix C must be minimal.
Dependencies
To enable this port, select the Use vehicle model parameter.
State-to-output matrix of ego vehicle predictive model. The number of columns in this signal must match the number of rows in Vehicle dynamics matrix A.
The ego vehicle predictive model defined by Vehicle dynamics matrix A, Vehicle dynamics matrix B, and Vehicle dynamics matrix C must be minimal.
Dependencies
To enable this port, select the Use vehicle model parameter.
Output
Front steering angle control signal in radians generated by the controller. The front steering angle is the angle of the front tires from the longitudinal axis of the vehicle. The steering angle is positive towards the positive lateral axis of the ego vehicle.
Parameters
Parameters Tab
Ego Vehicle
Select this parameter to define the ego vehicle model used by the MPC controller by specifying properties of the ego vehicle. The ego vehicle model is the linear model from the front steering angle to the lateral velocity and yaw angle rate. For more information, see Ego Vehicle Predictive Model.
To define the vehicle model, specify the following block parameters:
Total mass
Yaw moment of inertia
Longitudinal distance from center of gravity to front tires
Longitudinal distance from center of gravity to rear tires
Cornering stiffness of front tires
Cornering stiffness of rear tires
For more information on the ego vehicle model, see Ego Vehicle Predictive Model.
Selecting this parameter clears the Use vehicle model parameter.
Programmatic Use
Block Parameter:
ModelType |
| Type: string, character vector |
Default:
"Use vehicle parameters" |
Select this parameter to define the state-space matrices of the ego vehicle model used by the MPC controller. This model is the linear model from the front steering angle in radians to the lateral velocity in meters per second and yaw angle rate in radians per second. For more information on the ego vehicle model, see Ego Vehicle Predictive Model.
To define the initial internal model, specify the A, B, and C state-space matrices. The internal model must be a minimal realization with no direct feedthrough, and the dimensions of A, B, and C must be consistent.
Typically, the ego vehicle steering model is velocity-dependent, and therefore, it varies over time. To update the internal model at run time, use the Vehicle dynamics A, Vehicle dynamics B, and Vehicle dynamics C input ports.
Selecting this parameter clears the Use vehicle parameters parameter.
Programmatic Use
Block Parameter:
ModelType |
| Type: string, character vector |
Default:
"Use vehicle parameters" |
Ego vehicle mass in kg.
Dependencies
To enable this parameter, select the Use vehicle parameters parameter.
Programmatic Use
Block Parameter:
VehicleMass |
| Type: string, character vector |
Default:
"1575" |
Moment of inertia about the ego vehicle vertical axis in Kg·m2.
Dependencies
To enable this parameter, select the Use vehicle parameters parameter.
Programmatic Use
Block
Parameter:
VehicleYawInertia |
| Type: string, character vector |
Default:
"2875" |
Distance from the ego vehicle center of mass to its front tires in meters, measured along the longitudinal axis of the vehicle.
Dependencies
To enable this parameter, select the Use vehicle parameters parameter.
Programmatic Use
Block Parameter:
LengthToFront |
| Type: string, character vector |
Default:
"1.2" |
Distance from the ego vehicle center of mass to its rear tires in meters, measured along the longitudinal axis of the vehicle.
Dependencies
To enable this parameter, select the Use vehicle parameters parameter.
Programmatic Use
Block Parameter:
LengthToRear |
| Type: string, character vector |
Default:
"1.6" |
Front tire stiffness in N/rad, defined as the relationship between the side force on the front tires and the angle of the tires to the longitudinal axis of the vehicle.
Dependencies
To enable this parameter, select the Use vehicle parameters parameter.
Programmatic Use
Block Parameter:
FrontTireStiffness |
| Type: string, character vector |
Default:
"19000" |
Rear tire stiffness in N/rad, defined as the relationship between the side force on the rear tires and the angle of the tires to the longitudinal axis of the vehicle.
Dependencies
To enable this parameter, select the Use vehicle parameters parameter.
Programmatic Use
Block Parameter:
RearTireStiffness |
| Type: string, character vector |
Default:
"33000" |
Initial state matrix of ego vehicle predictive model. The number of rows in the state matrix corresponds to the number of states in the predictive model. This matrix must be square.
The initial ego vehicle predictive model defined by A, B, and C must be minimal.
Typically, the ego vehicle model varies over time. To update the state matrix at run time, use the Vehicle dynamics A input port.
Dependencies
To enable this parameter, select the Use vehicle model parameter.
Programmatic Use
Block Parameter:
EgoModelMatrixA |
| Type: string, character vector |
Default:
"[-4.4021
,-12.4603;1.3913,-5.1868]" |
Initial input-to-state matrix of ego vehicle predictive model. The number of rows in this parameter must match the number of rows in A.
The initial ego vehicle predictive model defined by A, B, and C must be minimal.
Typically, the ego vehicle model varies over time. To update the input-to-state matrix at run time, use the Vehicle dynamics B input port.
Dependencies
To enable this parameter, select the Use vehicle model parameter.
Programmatic Use
Block Parameter:
EgoModelMatrixB |
| Type: string, character vector |
Default:
"[24.1270;15.8609]" |
Initial state-to-output matrix of ego vehicle predictive model. The number of columns in this parameter must match the number of rows in A.
The initial ego vehicle predictive model defined by A, B, and C must be minimal.
Typically, the ego vehicle model varies over time. To update the state-to-output matrix at run time, use the Vehicle dynamics C input port.
Dependencies
To enable this parameter, select the Use vehicle model parameter.
Programmatic Use
Block Parameter:
EgoModelMatrixC |
| Type: string, character vector |
Default:
"[1,0;0,1]" |
Initial velocity of the ego vehicle model when the lane-keeping assist is enabled in m/s. This velocity can differ from the actual ego vehicle initial velocity.
Note
A very small initial velocity, for example eps,
can produce a nonminimal realization for the controller plant model,
causing an error. To prevent this error, set the initial velocity to
a larger value, for example 1e-3.
Programmatic Use
Block Parameter:
InitialLongVel |
| Type: string, character vector |
Default:
"15" |
Total transport lag, τ, in the ego vehicle model in seconds. This lag includes actuator, sensor, and communication lags. For each input-output channel, the transport lag is approximated by:
Programmatic Use
Block Parameter:
TransportLag |
| Type: string, character vector |
Default:
"0" |
Lane Keeping Controller Constraints
Minimum front steering angle constraint in radians.
If the minimum steering angle varies over time, add the Minimum steering angle input port to the block by selecting Use external source.
Dependencies
This parameter must be less than the Maximum steering angle parameter.
Programmatic Use
Block
Parameter:
MinSteering |
| Type: string, character vector |
Default:
"-0.26" |
Maximum front steering angle constraint in radians.
If the maximum steering angle varies over time, add the Maximum steering angle input port to the block by selecting Use external source.
Dependencies
This parameter must be greater than the Minimum steering angle parameter.
Programmatic Use
Block
Parameter:
MaxSteering |
| Type: string, character vector |
Default:
"0.26" |
Model Predictive Controller Settings
Controller sample time in seconds.
Programmatic Use
Block Parameter:
Ts |
| Type: string, character vector |
Default:
"0.1" |
Controller prediction horizon steps. The controller prediction time is the product of the sample time and the prediction horizon.
Programmatic Use
Block Parameter:
PredictionHorizon |
| Type: string, character vector |
Default:
"30" |
Closed-loop controller performance. The default parameter value provides a balanced controller design. Specifying a:
Smaller value produces a more robust controller with smoother control actions.
Larger value produces a more aggressive controller with a faster response time.
When you modify this parameter, the change is applied to the controller immediately.
Programmatic Use
Block Parameter:
ControllerBehavior |
| Type: string, character vector |
Default:
"0.5" |
Block Tab
Configure the controller to apply a suboptimal solution after a specified maximum number of iterations, which guarantees the worst-case execution time for your controller.
For more information, see Suboptimal QP Solution.
Dependencies
After selecting this parameter, specify the Maximum iteration number parameter.
Programmatic Use
Block Parameter:
suboptimal |
| Type: string, character vector |
Default:
"off" |
Maximum number of controller optimization iterations.
Dependencies
To enable this parameter, select the Use suboptimal solution parameter.
Programmatic Use
Block
Parameter:
maxiter |
| Type: string, character vector |
Default:
"10" |
To add the Enable optimization input port to the block, select this parameter.
Programmatic Use
Block
Parameter:
optmode |
| Type: string, character vector |
Default:
"off" |
To add the External control signal input port to the block, select this parameter.
Programmatic Use
Block Parameter:
trackmode |
| Type: string, character vector |
Default:
"off" |
Generate a custom LKA subsystem, which you can modify for your application. The controller configuration data for the custom controller is exported to the MATLAB® workspace as a structure.
You can modify the custom controller subsystem to:
Modify default MPC settings or use advanced MPC features.
Modify the default controller initial conditions.
Algorithms
The default ego vehicle predictive model is the following state-space model:
Here:
VX is the longitudinal velocity of the car. At the start of the simulation, this velocity is equal to the Initial condition for longitudinal velocity parameter. At run time, this velocity is equal to the Longitudinal velocity input signal.
m is the Total mass parameter.
IZ is the Yaw moment of inertia parameter.
LF is the Longitudinal distance from center of gravity to front tires parameter.
LR is the Longitudinal distance from center of gravity to rear tires parameter.
CF is the Cornering stiffness of front tires parameter.
CR is the Cornering stiffness of rear tires parameter.
The input to this model is the steering angle in radians, and the outputs are the lateral velocity in meters per second and yaw angle rate in radians per second.
To define a different ego vehicle predictive model, select the Use vehicle model parameter, and specify the initial state-space model. Then, specify the run-time values of the state-space matrices using the Vehicle dynamics A, Vehicle dynamics B, and Vehicle dynamics C input signals.
The controller creates its internal predictive model by augmenting the ego vehicle dynamic model. The augmented model includes the road curvature as a measured disturbance input signal.
By default, the model predictive controller assumes the following initial conditions for the ego vehicle:
Longitudinal velocity is equal to the Initial longitudinal velocity parameter.
Lateral velocity is zero.
Steering angle is zero.
Yaw angle rate is zero.
If the initial conditions in your model do not match these conditions, the Steering angle output can exhibit an initial bump at the start of the simulation.
To modify the controller initial conditions to match your simulation, create a custom lane-keeping control system by, on the Block tab, clicking Create LKA subsystem.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Version History
Introduced in R2018a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleziona un sito web
Seleziona un sito web per visualizzare contenuto tradotto dove disponibile e vedere eventi e offerte locali. In base alla tua area geografica, ti consigliamo di selezionare: .
Puoi anche selezionare un sito web dal seguente elenco:
Come ottenere le migliori prestazioni del sito
Per ottenere le migliori prestazioni del sito, seleziona il sito cinese (in cinese o in inglese). I siti MathWorks per gli altri paesi non sono ottimizzati per essere visitati dalla tua area geografica.
Americhe
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)

