Constrained Nonlinear Optimization Algorithms
Constrained Optimization Definition
Constrained minimization is the problem of finding a vector x that is a local minimum to a scalar function f(x) subject to constraints on the allowable x:
such that one or more of the following holds: c(x) ≤ 0, ceq(x) = 0, A·x ≤ b, Aeq·x = beq, l ≤ x ≤ u. There are even more constraints used in semi-infinite programming; see fseminf Problem Formulation and Algorithm.
fmincon Trust Region Reflective Algorithm
Trust-Region Methods for Nonlinear Minimization
Many of the methods used in Optimization Toolbox™ solvers are based on trust regions, a simple yet powerful concept in optimization.
To understand the trust-region approach to optimization, consider the unconstrained minimization problem, minimize f(x), where the function takes vector arguments and returns scalars. Suppose you are at a point x in n-space and you want to improve, i.e., move to a point with a lower function value. The basic idea is to approximate f with a simpler function q, which reasonably reflects the behavior of function f in a neighborhood N around the point x. This neighborhood is the trust region. A trial step s is computed by minimizing (or approximately minimizing) over N. This is the trust-region subproblem,
| (1) |
The current point is updated to be x + s if f(x + s) < f(x); otherwise, the current point remains unchanged and N, the region of trust, is shrunk and the trial step computation is repeated.
The key questions in defining a specific trust-region approach to minimizing f(x) are how to choose and compute the approximation q (defined at the current point x), how to choose and modify the trust region N, and how accurately to solve the trust-region subproblem. This section focuses on the unconstrained problem. Later sections discuss additional complications due to the presence of constraints on the variables.
In the standard trust-region method ([48]), the quadratic approximation q is defined by the first two terms of the Taylor approximation to F at x; the neighborhood N is usually spherical or ellipsoidal in shape. Mathematically the trust-region subproblem is typically stated
| (2) |
where g is the gradient of f at the current point x, H is the Hessian matrix (the symmetric matrix of second derivatives), D is a diagonal scaling matrix, Δ is a positive scalar, and ‖ . ‖ is the 2-norm. Good algorithms exist for solving Equation 2 (see [48]); such algorithms typically involve the computation of all eigenvalues of H and a Newton process applied to the secular equation
Such algorithms provide an accurate solution to Equation 2. However, they require time proportional to several factorizations of H. Therefore, for large-scale problems a different approach is needed. Several approximation and heuristic strategies, based on Equation 2, have been proposed in the literature ([42] and [50]). The approximation approach followed in Optimization Toolbox solvers is to restrict the trust-region subproblem to a two-dimensional subspace S ([39] and [42]). Once the subspace S has been computed, the work to solve Equation 2 is trivial even if full eigenvalue/eigenvector information is needed (since in the subspace, the problem is only two-dimensional). The dominant work has now shifted to the determination of the subspace.
The two-dimensional subspace S is determined with the aid of a preconditioned conjugate gradient process described below. The solver defines S as the linear space spanned by s1 and s2, where s1 is in the direction of the gradient g, and s2 is either an approximate Newton direction, i.e., a solution to
| (3) |
or a direction of negative curvature,
| (4) |
The philosophy behind this choice of S is to force global convergence (via the steepest descent direction or negative curvature direction) and achieve fast local convergence (via the Newton step, when it exists).
A sketch of unconstrained minimization using trust-region ideas is now easy to give:
Formulate the two-dimensional trust-region subproblem.
Solve Equation 2 to determine the trial step s.
If f(x + s) < f(x), then x = x + s.
Adjust Δ.
These four steps are repeated until convergence. The trust-region dimension Δ is adjusted according to standard rules. In particular, it is decreased if the trial step is not accepted, i.e., f(x + s) ≥ f(x). See [46] and [49] for a discussion of this aspect.
Optimization Toolbox solvers treat a few important special cases of f with specialized functions: nonlinear least-squares, quadratic functions, and linear least-squares. However, the underlying algorithmic ideas are the same as for the general case. These special cases are discussed in later sections.
Preconditioned Conjugate Gradient Method
A popular way to solve large, symmetric, positive definite systems of linear equations Hp = –g is the method of Preconditioned Conjugate Gradients (PCG). This iterative approach requires the ability to calculate matrix-vector products of the form H·v where v is an arbitrary vector. The symmetric positive definite matrix M is a preconditioner for H. That is, M = C2, where C–1HC–1 is a well-conditioned matrix or a matrix with clustered eigenvalues.
In a minimization context, you can assume that the Hessian matrix H is symmetric. However, H is guaranteed to be positive definite only in the neighborhood of a strong minimizer. Algorithm PCG exits when it encounters a direction of negative (or zero) curvature, that is, dTHd ≤ 0. The PCG output direction p is either a direction of negative curvature or an approximate solution to the Newton system Hp = –g. In either case, p helps to define the two-dimensional subspace used in the trust-region approach discussed in Trust-Region Methods for Nonlinear Minimization.
Linear Equality Constraints
Linear constraints complicate the situation described for unconstrained minimization. However, the underlying ideas described previously can be carried through in a clean and efficient way. The trust-region methods in Optimization Toolbox solvers generate strictly feasible iterates.
The general linear equality constrained minimization problem can be written
| (5) |
where A is an m-by-n matrix (m ≤ n). Some Optimization Toolbox solvers preprocess A to remove strict linear dependencies using a technique based on the LU factorization of AT [46]. Here A is assumed to be of rank m.
The method used to solve Equation 5 differs from the unconstrained approach in two significant ways. First, an initial feasible point x0 is computed, using a sparse least-squares step, so that Ax0 = b. Second, Algorithm PCG is replaced with Reduced Preconditioned Conjugate Gradients (RPCG), see [46], in order to compute an approximate reduced Newton step (or a direction of negative curvature in the null space of A). The key linear algebra step involves solving systems of the form
| (6) |
where approximates A (small nonzeros of A are set to zero provided rank is not lost) and C is a sparse symmetric positive-definite approximation to H, i.e., C = H. See [46] for more details.
Box Constraints
The box constrained problem is of the form
| (7) |
where l is a vector of lower bounds, and u is a vector of upper bounds. Some (or all) of the components of l can be equal to –∞ and some (or all) of the components of u can be equal to ∞. The method generates a sequence of strictly feasible points. Two techniques are used to maintain feasibility while achieving robust convergence behavior. First, a scaled modified Newton step replaces the unconstrained Newton step (to define the two-dimensional subspace S). Second, reflections are used to increase the step size.
The scaled modified Newton step arises from examining the Kuhn-Tucker necessary conditions for Equation 7,
| (8) |
where
and the vector v(x) is defined below, for each 1 ≤ i ≤ n:
If gi < 0 and ui < ∞ then vi = xi – ui
If gi ≥ 0 and li > –∞ then vi = xi – li
If gi < 0 and ui = ∞ then vi = –1
If gi ≥ 0 and li = –∞ then vi = 1
The nonlinear system Equation 8 is not differentiable everywhere. Nondifferentiability occurs when vi = 0. You can avoid such points by maintaining strict feasibility, i.e., restricting l < x < u.
The scaled modified Newton step sk for the nonlinear system of equations given by Equation 8 is defined as the solution to the linear system
| (9) |
at the kth iteration, where
| (10) |
and
| (11) |
Here Jv plays the role of the Jacobian of |v|. Each diagonal component of the diagonal matrix Jv equals 0, –1, or 1. If all the components of l and u are finite, Jv = diag(sign(g)). At a point where gi = 0, vi might not be differentiable. is defined at such a point. Nondifferentiability of this type is not a cause for concern because, for such a component, it is not significant which value vi takes. Further, |vi| will still be discontinuous at this point, but the function |vi|·gi is continuous.
Second, reflections are used to increase the step size. A (single) reflection step is defined as follows. Given a step p that intersects a bound constraint, consider the first bound constraint crossed by p; assume it is the ith bound constraint (either the ith upper or ith lower bound). Then the reflection step pR = p except in the ith component, where pRi = –pi.
fmincon Active Set Algorithm
Introduction
In constrained optimization, the general aim is to transform the problem into an easier subproblem that can then be solved and used as the basis of an iterative process. A characteristic of a large class of early methods is the translation of the constrained problem to a basic unconstrained problem by using a penalty function for constraints that are near or beyond the constraint boundary. In this way the constrained problem is solved using a sequence of parametrized unconstrained optimizations, which in the limit (of the sequence) converge to the constrained problem. These methods are now considered relatively inefficient and have been replaced by methods that have focused on the solution of the Karush-Kuhn-Tucker (KKT) equations. The KKT equations are necessary conditions for optimality for a constrained optimization problem. If the problem is a so-called convex programming problem, that is, f(x) and Gi(x), i = 1,...,m, are convex functions, then the KKT equations are both necessary and sufficient for a global solution point.
Referring to GP (Equation 1), the Kuhn-Tucker equations can be stated as
| (12) |
in addition to the original constraints in Equation 1.
The first equation describes a canceling of the gradients between the objective function and the active constraints at the solution point. For the gradients to be canceled, Lagrange multipliers (λi, i = 1,...,m) are necessary to balance the deviations in magnitude of the objective function and constraint gradients. Because only active constraints are included in this canceling operation, constraints that are not active must not be included in this operation and so are given Lagrange multipliers equal to 0. This is stated implicitly in the last two Kuhn-Tucker equations.
The solution of the KKT equations forms the basis to many nonlinear programming algorithms. These algorithms attempt to compute the Lagrange multipliers directly. Constrained quasi-Newton methods guarantee superlinear convergence by accumulating second-order information regarding the KKT equations using a quasi-Newton updating procedure. These methods are commonly referred to as Sequential Quadratic Programming (SQP) methods, since a QP subproblem is solved at each major iteration (also known as Iterative Quadratic Programming, Recursive Quadratic Programming, and Constrained Variable Metric methods).
The 'active-set' algorithm cannot use sparse data; see Sparsity in Optimization Algorithms.
Sequential Quadratic Programming (SQP)
SQP methods represent the state of the art in nonlinear programming methods. Schittkowski [36], for example, has implemented and tested a version that outperforms every other tested method in terms of efficiency, accuracy, and percentage of successful solutions, over a large number of test problems.
Based on the work of Biggs [1], Han [22], and Powell ([32] and [33]), the method allows you to closely mimic Newton's method for constrained optimization just as is done for unconstrained optimization. At each major iteration, an approximation is made of the Hessian of the Lagrangian function using a quasi-Newton updating method. This is then used to generate a QP subproblem whose solution is used to form a search direction for a line search procedure. An overview of SQP is found in Fletcher [13], Gill et al. [19], Powell [35], and Schittkowski [23]. The general method, however, is stated here.
Given the problem description in GP (Equation 1) the principal idea is the formulation of a QP subproblem based on a quadratic approximation of the Lagrangian function.
| (13) |
Here you simplify Equation 1 by assuming that bound constraints have been expressed as inequality constraints. You obtain the QP subproblem by linearizing the nonlinear constraints.
Quadratic Programming (QP) Subproblem
| (14) |
This subproblem can be solved using any QP algorithm (see, for instance, Quadratic Programming Solution). The solution is used to form a new iterate
xk + 1 = xk + αkdk.
The step length parameter αk is determined by an appropriate line search procedure so that a sufficient decrease in a merit function is obtained (see Updating the Hessian Matrix). The matrix Hk is a positive definite approximation of the Hessian matrix of the Lagrangian function (Equation 13). Hk can be updated by any of the quasi-Newton methods, although the BFGS method (see Updating the Hessian Matrix) appears to be the most popular.
A nonlinearly constrained problem can often be solved in fewer iterations than an unconstrained problem using SQP. One of the reasons for this is that, because of limits on the feasible area, the optimizer can make informed decisions regarding directions of search and step length.
Consider Rosenbrock's function with an additional nonlinear inequality constraint, g(x),
| (15) |
This was solved by an SQP implementation in 31 iterations compared to 37 for the unconstrained case. The figure shows the path to the solution point x = [0.9072,0.8228] starting at x = [–1.9,2.0].
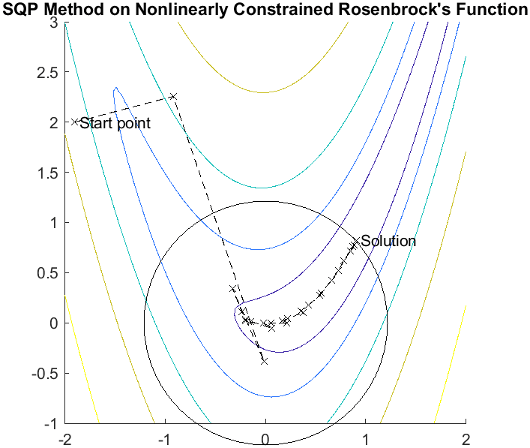
SQP Implementation
The SQP implementation consists of three main stages, which are discussed briefly in the following subsections:
Updating the Hessian Matrix. At each major iteration a positive definite quasi-Newton approximation of the Hessian of the Lagrangian function, H, is calculated using the BFGS method, where λi, i = 1,...,m, is an estimate of the Lagrange multipliers.
| (16) |
where
Powell [33] recommends keeping the Hessian positive definite even though it might be positive indefinite at the solution point. A positive definite Hessian is maintained providing is positive at each update and that H is initialized with a positive definite matrix. When is not positive, qk is modified on an element-by-element basis so that . The general aim of this modification is to distort the elements of qk, which contribute to a positive definite update, as little as possible. Therefore, in the initial phase of the modification, the most negative element of qk*sk is repeatedly halved. This procedure is continued until is greater than or equal to a small negative tolerance. If, after this procedure, is still not positive, modify qk by adding a vector v multiplied by a constant scalar w, that is,
| (17) |
where
and increase w systematically until becomes positive.
The functions fmincon, fminimax, fgoalattain,
and fseminf all use SQP. If Display is
set to 'iter' in options, then
various information is given such as function values and the maximum
constraint violation. When the Hessian has to be modified using the
first phase of the preceding procedure to keep it positive definite,
then Hessian modified is displayed. If the Hessian
has to be modified again using the second phase of the approach described
above, then Hessian modified twice is displayed.
When the QP subproblem is infeasible, then infeasible is displayed. Such displays
are usually not a cause for concern but indicate that the problem
is highly nonlinear and that convergence might take longer than usual.
Sometimes the message no update is displayed, indicating that is nearly zero. This can be
an indication that the problem setup is wrong or you are trying to
minimize a noncontinuous function.
Quadratic Programming Solution. At each major iteration of the SQP method,
a QP problem of the following form is solved, where Ai refers
to the ith row of the m-by-n matrix A.
| (18) |
The method used in Optimization Toolbox functions is an active set strategy (also known as a projection method) similar to that of Gill et al., described in [18] and [17]. It has been modified for both Linear Programming (LP) and Quadratic Programming (QP) problems.
The solution procedure involves two phases. The first phase involves the calculation of a feasible point (if one exists). The second phase involves the generation of an iterative sequence of feasible points that converge to the solution. In this method an active set, , is maintained that is an estimate of the active constraints (i.e., those that are on the constraint boundaries) at the solution point. Virtually all QP algorithms are active set methods. This point is emphasized because there exist many different methods that are very similar in structure but that are described in widely different terms.
is updated at each iteration k, and this is used to form a basis for a search direction . Equality constraints always remain in the active set . The notation for the variable is used here to distinguish it from dk in the major iterations of the SQP method. The search direction is calculated and minimizes the objective function while remaining on any active constraint boundaries. The feasible subspace for is formed from a basis Zk whose columns are orthogonal to the estimate of the active set (i.e., ). Thus a search direction, which is formed from a linear summation of any combination of the columns of Zk, is guaranteed to remain on the boundaries of the active constraints.
The matrix Zk is formed from the last m – l columns of the QR decomposition of the matrix , where l is the number of active constraints and l < m. That is, Zk is given by
| (19) |
where
Once Zk is found, a new search direction is sought that minimizes q(d) where is in the null space of the active constraints. That is, is a linear combination of the columns of Zk: for some vector p.
Then if you view the quadratic as a function of p, by substituting for , you have
| (20) |
Differentiating this with respect to p yields
| (21) |
∇q(p) is referred to as the projected gradient of the quadratic function because it is the gradient projected in the subspace defined by Zk. The term is called the projected Hessian. Assuming the Hessian matrix H is positive definite (which is the case in this implementation of SQP), then the minimum of the function q(p) in the subspace defined by Zk occurs when ∇q(p) = 0, which is the solution of the system of linear equations
| (22) |
A step is then taken of the form
| (23) |
At each iteration, because of the quadratic nature of the objective function, there are only two choices of step length α. A step of unity along is the exact step to the minimum of the function restricted to the null space of . If such a step can be taken, without violation of the constraints, then this is the solution to QP (Equation 18). Otherwise, the step along to the nearest constraint is less than unity and a new constraint is included in the active set at the next iteration. The distance to the constraint boundaries in any direction is given by
| (24) |
which is defined for constraints not in the active set, and where the direction is towards the constraint boundary, i.e., .
When n independent constraints are included in the active set, without location of the minimum, Lagrange multipliers, λk, are calculated that satisfy the nonsingular set of linear equations
| (25) |
If all elements of λk are positive, xk is the optimal solution of QP (Equation 18). However, if any component of λk is negative, and the component does not correspond to an equality constraint, then the corresponding element is deleted from the active set and a new iterate is sought.
Initialization. The algorithm requires a feasible point to start. If the current point from the SQP method is not feasible, then you can find a point by solving the linear programming problem
| (26) |
The notation Ai indicates the ith row of the matrix A. You can find a feasible point (if one exists) to Equation 26 by setting x to a value that satisfies the equality constraints. You can determine this value by solving an under- or overdetermined set of linear equations formed from the set of equality constraints. If there is a solution to this problem, then the slack variable γ is set to the maximum inequality constraint at this point.
You can modify the preceding QP algorithm for LP problems by setting the search direction to the steepest descent direction at each iteration, where gk is the gradient of the objective function (equal to the coefficients of the linear objective function).
| (27) |
If a feasible point is found using the preceding LP method, the main QP phase is entered. The search direction is initialized with a search direction found from solving the set of linear equations
| (28) |
where gk is the gradient of the objective function at the current iterate xk (i.e., Hxk + c).
If a feasible solution is not found for the QP problem, the direction of search for the main SQP routine is taken as one that minimizes γ.
Line Search and Merit Function. The solution to the QP subproblem produces a vector dk, which is used to form a new iterate
| (29) |
The step length parameter αk is determined in order to produce a sufficient decrease in a merit function. The merit function used by Han [22] and Powell [33] of the following form is used in this implementation.
| (30) |
Powell recommends setting the penalty parameter
| (31) |
This allows positive contribution from constraints that are inactive in the QP solution but were recently active. In this implementation, the penalty parameter ri is initially set to
| (32) |
where represents the Euclidean norm.
This ensures larger contributions to the penalty parameter from constraints with smaller gradients, which would be the case for active constraints at the solution point.
fmincon SQP Algorithm
The sqp algorithm (and nearly identical sqp-legacy algorithm)
is similar to the active-set algorithm (for a description,
see fmincon Active Set Algorithm).
The basic sqp algorithm is described in Chapter
18 of Nocedal and Wright [31].
The sqp algorithm is essentially the same
as the sqp-legacy algorithm, but has a different
implementation. Usually, sqp has faster execution
time and less memory usage than sqp-legacy.
The most important differences between the sqp and
the active-set algorithms are:
Strict Feasibility With Respect to Bounds
The sqp algorithm takes every iterative step
in the region constrained by bounds. Furthermore, finite difference
steps also respect bounds. Bounds are not strict; a step can be exactly
on a boundary. This strict feasibility can be beneficial when your
objective function or nonlinear constraint functions are undefined
or are complex outside the region constrained by bounds.
Robustness to Non-Double Results
During its iterations, the sqp algorithm
can attempt to take a step that fails. This means an objective function
or nonlinear constraint function you supply returns a value of Inf, NaN,
or a complex value. In this case, the algorithm attempts to take a
smaller step.
Refactored Linear Algebra Routines
The sqp algorithm uses a different set of
linear algebra routines to solve the quadratic programming subproblem, Equation 14. These routines
are more efficient in both memory usage and speed than the active-set routines.
Reformulated Feasibility Routines
The sqp algorithm has two new approaches
to the solution of Equation 14 when constraints are not satisfied.
The
sqpalgorithm combines the objective and constraint functions into a merit function. The algorithm attempts to minimize the merit function subject to relaxed constraints. This modified problem can lead to a feasible solution. However, this approach has more variables than the original problem, so the problem size in Equation 14 increases. The increased size can slow the solution of the subproblem. These routines are based on the articles by Spellucci [60] and Tone [61]. Thesqpalgorithm sets the penalty parameter for the merit function Equation 30 according to the suggestion in [41].Suppose nonlinear constraints are not satisfied, and an attempted step causes the constraint violation to grow. The
sqpalgorithm attempts to obtain feasibility using a second-order approximation to the constraints. The second-order technique can lead to a feasible solution. However, this technique can slow the solution by requiring more evaluations of the nonlinear constraint functions.
fmincon Interior Point Algorithm
Barrier Function
The interior-point approach to constrained minimization is to solve a sequence of approximate minimization problems. The original problem is
| (33) |
| (34) |
The approximate problem Equation 34 is a sequence of equality constrained problems. These are easier to solve than the original inequality-constrained problem Equation 33.
To solve the approximate problem, the algorithm uses one of two main types of steps at each iteration:
A direct step in (x, s). This step attempts to solve the KKT equations, Equation 2 and Equation 3, for the approximate problem via a linear approximation. This is also called a Newton step.
By default, the algorithm first attempts to take a direct step. If it cannot, it attempts a CG step. One case where it does not take a direct step is when the approximate problem is not locally convex near the current iterate.
At each iteration the algorithm decreases a merit function, such as
| (35) |
If either the objective function or a nonlinear constraint function returns a
complex value, NaN, Inf, or an error at an iterate
xj, the algorithm rejects
xj. The rejection has the same
effect as if the merit function did not decrease sufficiently: the algorithm
then attempts a different, shorter step. Wrap any code that can error in
try-catch:
function val = userFcn(x)
try
val = ... % code that can error
catch
val = NaN;
endThe objective and constraints must yield proper (double)
values at the initial point.
Direct Step
The following variables are used in defining the direct step:
H denotes the Hessian of the Lagrangian of fμ:
(36) Jg denotes the Jacobian of the constraint function g.
Jh denotes the Jacobian of the constraint function h.
S = diag(s).
λ denotes the Lagrange multiplier vector associated with constraints g
Λ = diag(λ).
y denotes the Lagrange multiplier vector associated with h.
e denote the vector of ones the same size as g.
Equation 38 defines the direct step (Δx, Δs):
| (37) |
This equation comes directly from attempting to solve Equation 2 and Equation 3 using a linearized Lagrangian.
You can symmetrize the equation by premultiplying the second variable Δs by S–1:
| (38) |
In order to solve this equation for (Δx, Δs), the algorithm makes an LDL factorization of the matrix; see
ldl. This is the most
computationally expensive step. One result of this factorization is a
determination of whether the projected Hessian is positive definite or not; if
not, the algorithm uses a conjugate gradient step, described in Conjugate Gradient Step.
Update Barrier Parameter
For the approximate problem Equation 34 to approach the original problem, the
barrier parameter μ needs to decrease toward 0 as the
iterations proceed. The algorithm has two barrier parameter update options,
which you specify using the BarrierParamUpdate option:
'monotone' (default) and
'predictor-corrector'.
The 'monotone' option decreases the parameter
μ by a factor of 1/100 or 1/5 when the approximate
problem is solved with sufficient accuracy in the previous iteration. The option
uses a factor of 1/100 when the algorithm takes only one or two iterations to
achieve sufficient accuracy, and uses 1/5 otherwise. The measure of accuracy is
the following test, which determines if the size of all terms on the right side
of Equation 38 is less than μ:
Note
fmincon overrides the
BarrierParamUpdate setting to
'monotone' in either of these cases:
The problem has no inequality constraints, including bound constraints.
The
SubproblemAlgorithmoption is'cg'.
The 'predictor-corrector' algorithm for updating the
barrier parameter μ is similar to the linear programming
Predictor-Corrector algorithm.
Predictor-corrector steps can accelerate the existing Fiacco-McCormick (monotone) approach by adjusting for the linearization error in the Newton steps. The effects of the predictor-corrector algorithm are twofold: it often improves step directions and simultaneously updates the barrier parameter adaptively with the centering parameter σ to encourage iterates to follow the central path. See Nocedal and Wright’s [31] discussion of predictor-corrector steps for linear programs to understand why the central path allows larger step sizes and, consequently, faster convergence.
The predictor step uses the linearized step with μ = 0, meaning without a barrier function:
Define ɑs and ɑλ to be the largest step sizes that do not violate the nonnegativity constraints.
Now compute the complementarity from the predictor step.
| (39) |
where m is the number of constraints.
The first corrector step adjusts for the quadratic term neglected in the Newton root-finding linearization
To correct the quadratic error, solve the linear system for the corrector step direction.
The second corrector step is a centering step. The centering correction is based on the variable σ on the right side of the equation
Here, σ is defined as
where μP is defined in equation Equation 39, and .
To prevent the barrier parameter from decreasing too quickly, potentially destabilizing the algorithm, the algorithm keeps the centering parameter σ above 1/100. This action causes the barrier parameter μ to decrease by no more than a factor of 1/100.
Algorithmically, the first correction and centering steps are independent of each other, so they are computed together. Furthermore, the matrix on the left for the predictor and both corrector steps is the same. So, algorithmically, the matrix is factorized once, and this factorization is used for all these steps.
The algorithm can reject the proposed predictor-corrector step when the step increases the merit function value Equation 35, increases the complementarity by at least a factor of two, or the computed inertia is incorrect (the problem looks nonconvex). In these cases, the algorithm attempts to take a different step or a conjugate gradient step.
Conjugate Gradient Step
The conjugate gradient approach to solving the approximate problem Equation 34 is similar to other conjugate gradient calculations. In this case, the algorithm adjusts both x and s, keeping the slacks s positive. The approach is to minimize a quadratic approximation to the approximate problem in a trust region, subject to linearized constraints.
Specifically, let R denote the radius of the trust region, and let other variables be defined as in Direct Step. The algorithm obtains Lagrange multipliers by approximately solving the KKT equations
in the least-squares sense, subject to λ being positive. Then it takes a step (Δx, Δs) to approximately solve
| (40) |
| (41) |
Feasibility Mode
When the EnableFeasibilityMode option is
true and the iterations do not decrease the infeasibility
quickly enough, the algorithm switches to feasibility mode. This switch happens
after the algorithm fails to decrease the infeasibility in normal mode, and then
fails again after switching to conjugate gradient mode. Therefore, for best
performance when the solver fails to find a feasible solution without
feasibility mode, set the SubproblemAlgorithm to
'cg' when using feasibility mode. Doing so avoids
fruitless searching in normal mode.
The feasibility mode algorithm is based on Nocedal, Öztoprak, and Waltz [1]. The algorithm ignores the objective function and instead tries to minimize the infeasibility, defined as the sum of the positive parts of the inequality constraint functions and the absolute value of the equality constraint functions. In terms of the relaxation variables , which correspond to inequalities, positive parts of equalities, and negative parts of equalities, respectively, the problem is
subject to the constraints
To solve the relaxed problem, the software uses an interior-point formulation with a logarithmic barrier function and the slacks to minimize
subject to the constraints
The solution process for the relaxed problem begins with μ initialized to the current barrier parameter value. The slack variable sI is initialized to the current inequality slack value, inherited from the main mode. The r variables are initialized to
The remaining slacks are initialized to
Starting at this initial point, the feasibility mode algorithm reuses the code for the normal interior-point algorithm. This process requires special step computations because the r variables are linear and, therefore, their associated second derivatives are zero. In other words, the objective function Hessian for the feasibility problem is rank-deficient. Therefore, the algorithm cannot take a Newton step. Instead, the algorithm takes a steepest-descent direction step. The algorithm starts with the gradient of the objective with respect to the variables, projects the gradient onto the null space of the Jacobian of the constraints, and rescales the resulting vector so that it has an appropriate step length. This step can be effective at reducing the infeasibility.
The feasibility mode algorithm ends when it reduces the infeasibility by a factor of 10. When feasibility mode ends, the algorithm passes the variables x and sI to the main algorithm, and discards the other slack variables and relaxation variables r.
References
[1] Nocedal, Jorge, Figen Öztoprak, and Richard A. Waltz. An Interior Point Method for Nonlinear Programming with Infeasibility Detection Capabilities. Optimization Methods & Software 29(4), July 2014, pp. 837–854.
Interior-Point Algorithm Options
Here are the meanings and effects of several options in the interior-point algorithm.
HonorBounds— When set totrue, every iterate satisfies the bound constraints you have set. When set tofalse, the algorithm may violate bounds during intermediate iterations.HessianApproximation— When set to:'bfgs',fminconcalculates the Hessian by a dense quasi-Newton approximation.'lbfgs',fminconcalculates the Hessian by a limited-memory, large-scale quasi-Newton approximation.'fin-diff-grads',fminconcalculates a Hessian-times-vector product by finite differences of the gradient(s); other options need to be set appropriately.
HessianFcn—fminconuses the function handle you specify inHessianFcnto compute the Hessian. See Including Hessians.HessianMultiplyFcn— Give a separate function for Hessian-times-vector evaluation. For details, see Including Hessians and Hessian Multiply Function.SubproblemAlgorithm— Determines whether or not to attempt the direct Newton step. The default setting'factorization'allows this type of step to be attempted. The setting'cg'allows only conjugate gradient steps.
For a complete list of options see Interior-Point Algorithm in fmincon
options.
fminbnd Algorithm
fminbnd is a solver available in any MATLAB® installation.
It solves for a local minimum in one dimension within a bounded interval.
It is not based on derivatives. Instead, it uses golden-section search
and parabolic interpolation.
fseminf Problem Formulation and Algorithm
fseminf Problem Formulation
fseminf addresses optimization problems
with additional types of constraints compared to those addressed by fmincon.
The formulation of fmincon is
such that c(x) ≤ 0, ceq(x) = 0, A·x ≤ b, Aeq·x = beq, and l ≤ x ≤ u.
fseminf adds the following set of semi-infinite
constraints to those already given. For wj in
a one- or two-dimensional bounded interval or rectangle Ij,
for a vector of continuous functions K(x, w),
the constraints are
Kj(x, wj) ≤ 0 for all wj∈Ij.
The term “dimension” of an fseminf problem
means the maximal dimension of the constraint set I:
1 if all Ij are intervals,
and 2 if at least one Ij is
a rectangle. The size of the vector of K does not
enter into this concept of dimension.
The reason this is called semi-infinite programming is that there are a finite number of variables (x and wj), but an infinite number of constraints. This is because the constraints on x are over a set of continuous intervals or rectangles Ij, which contains an infinite number of points, so there are an infinite number of constraints: Kj(x, wj) ≤ 0 for an infinite number of points wj.
You might think a problem with an infinite number of constraints
is impossible to solve. fseminf addresses this
by reformulating the problem to an equivalent one that has two stages:
a maximization and a minimization. The semi-infinite constraints are
reformulated as
| (42) |
where |K| is the number of components of the vector K; i.e., the number of semi-infinite constraint functions. For fixed x, this is an ordinary maximization over bounded intervals or rectangles.
fseminf further simplifies the problem
by making piecewise quadratic or cubic approximations κj(x, wj) to
the functions Kj(x, wj),
for each x that the solver visits. fseminf considers
only the maxima of the interpolation function κj(x, wj),
instead of Kj(x, wj),
in Equation 42. This
reduces the original problem, minimizing a semi-infinitely constrained
function, to a problem with a finite number of constraints.
Sampling Points. Your semi-infinite constraint function must provide a set of sampling points, points used in making the quadratic or cubic approximations. To accomplish this, it should contain:
The initial spacing
sbetween sampling points wA way of generating the set of sampling points w from
s
The initial spacing s is a |K|-by-2
matrix. The jth row of s represents
the spacing for neighboring sampling points for the constraint function Kj.
If Kj depends on a one-dimensional wj,
set s(j,2) = 0. fseminf updates
the matrix s in subsequent iterations.
fseminf uses the matrix s to
generate the sampling points w, which it then uses
to create the approximation κj(x, wj).
Your procedure for generating w from s should
keep the same intervals or rectangles Ij during
the optimization.
Example of Creating Sampling Points. Consider a problem with two semi-infinite constraints, K1 and K2. K1 has one-dimensional w1, and K2 has two-dimensional w2. The following code generates a sampling set from w1 = 2 to 12:
% Initial sampling interval
if isnan(s(1,1))
s(1,1) = .2;
s(1,2) = 0;
end
% Sampling set
w1 = 2:s(1,1):12;fseminf specifies s as NaN when
it first calls your constraint function. Checking for this allows
you to set the initial sampling interval.
The following code generates a sampling set from w2 in a square, with each component going from 1 to 100, initially sampled more often in the first component than the second:
% Initial sampling interval if isnan(s(1,1)) s(2,1) = 0.2; s(2,2) = 0.5; end % Sampling set w2x = 1:s(2,1):100; w2y = 1:s(2,2):100; [wx,wy] = meshgrid(w2x,w2y);
The preceding code snippets can be simplified as follows:
% Initial sampling interval
if isnan(s(1,1))
s = [0.2 0;0.2 0.5];
end
% Sampling set
w1 = 2:s(1,1):12;
w2x = 1:s(2,1):100;
w2y = 1:s(2,2):100;
[wx,wy] = meshgrid(w2x,w2y);fseminf Algorithm
fseminf essentially reduces the problem
of semi-infinite programming to a problem addressed by fmincon. fseminf takes
the following steps to solve semi-infinite programming problems:
At the current value of x,
fseminfidentifies all the wj,i such that the interpolation κj(x, wj,i) is a local maximum. (The maximum refers to varying w for fixed x.)fseminftakes one iteration step in the solution of thefminconproblem:such that c(x) ≤ 0, ceq(x) = 0, A·x ≤ b, Aeq·x = beq, and l ≤ x ≤ u, where c(x) is augmented with all the maxima of κj(x, wj) taken over all wj∈Ij, which is equal to the maxima over j and i of κj(x, wj,i).
fseminfchecks if any stopping criterion is met at the new point x (to halt the iterations); if not, it continues to step 4.fseminfchecks if the discretization of the semi-infinite constraints needs updating, and updates the sampling points appropriately. This provides an updated approximation κj(x, wj). Then it continues at step 1.
