adaptmesh

Create adaptive 2-D mesh and solve PDE

This page describes the legacy workflow. New features might not be compatible with the legacy workflow. In the recommended workflow, see generateMesh for mesh generation and solvepde for PDE solution.

Syntax

[u,p,e,t] = adaptmesh(g,b,c,a,f)

[u,p,e,t] = adaptmesh(g,b,c,a,f,Name,Value)

Description

[u,p,e,t] = adaptmesh(g,b,c,a,f) generates an adaptive [p,e,t] mesh and returns the solution u for an elliptic 2-D PDE problem

$$-\nabla \cdot \left(c\nabla u\right)+au=f$$

for (x,y) ∊ Ω, or the elliptic system PDE problem

$$-\nabla \cdot \left(c\otimes \nabla u\right)+au=f$$

with the problem geometry and boundary conditions given by g and b. The mesh is described by the p, e, and t matrices.

Upon termination, the function issues one of these messages:

• Adaption completed. (This means that the Tripick function returned zero triangles to refine.)

• Maximum number of triangles obtained.

• Maximum number of refinement passes obtained.

[u,p,e,t] = adaptmesh(g,b,c,a,f,Name,Value) performs adaptive mesh generation and PDE solution for elliptic 2-D PDE problems using one or more Name,Value pair arguments.

Examples

Adaptive Mesh Generation and Mesh Refinement

Solve the Laplace equation over a circle sector, with Dirichlet boundary conditions u = cos(2/3atan2(y,x)) along the arc and u = 0 along the straight lines, and compare the resulting solution to the exact solution. Set the options so that adaptmesh refines the triangles using the worst error criterion until it obtains a mesh with at least 500 triangles.

c45 = cos(pi/4);
L1 = [2 -c45 0  c45 0 1 0 0 0 0]';
L2 = [2 -c45 0 -c45 0 1 0 0 0 0]';
C1 = [1 -c45  c45 -c45 -c45 1 0 0 0 1]';
C2 = [1  c45  c45 -c45  c45 1 0 0 0 1]';
C3 = [1  c45 -c45  c45  c45 1 0 0 0 1]';
g = [L1 L2 C1 C2 C3];

[u,p,e,t] = adaptmesh(g,"cirsb",1,0,0,"Maxt",500,...
                     "Tripick","pdeadworst");

Number of triangles: 204
Number of triangles: 208
Number of triangles: 217
Number of triangles: 230
Number of triangles: 265
Number of triangles: 274
Number of triangles: 332
Number of triangles: 347
Number of triangles: 460
Number of triangles: 477
Number of triangles: 699

Maximum number of triangles obtained.

Find the maximal absolute error.

x = p(1,:); y = p(2,:);
exact = ((x.^2 + y.^2).^(1/3).*cos(2/3*atan2(y,x)))'; 
max(abs(u - exact))

ans = 
0.0028

Find the number of triangles.

size(t,2)

ans = 
699

Plot the mesh.

pdemesh(p,e,t)

Test how many refinements you need with a uniform triangle mesh.

[p,e,t] = initmesh(g); 
[p,e,t] = refinemesh(g,p,e,t); 
u = assempde("cirsb",p,e,t,1,0,0); 
x = p(1,:);
y = p(2,:); 
exact = ((x.^2 + y.^2).^(1/3).*cos(2/3*atan2(y,x)))'; 
max(abs(u - exact))

ans = 
0.0116

Find the number of triangles in this case.

size(t,2)

ans = 
816

Refine the mesh one more time. The maximal absolute error for uniform meshing is still greater than for adaptive meshing.

[p,e,t] = refinemesh(g,p,e,t); 
u = assempde("cirsb",p,e,t,1,0,0); 
x = p(1,:);
y = p(2,:); 
exact = ((x.^2 + y.^2).^(1/3).*cos(2/3*atan2(y,x)))'; 
max(abs(u - exact))

ans = 
0.0075

Find the number of triangles in this case.

size(t,2)

ans = 
3264

Plot the mesh.

pdemesh(p,e,t)

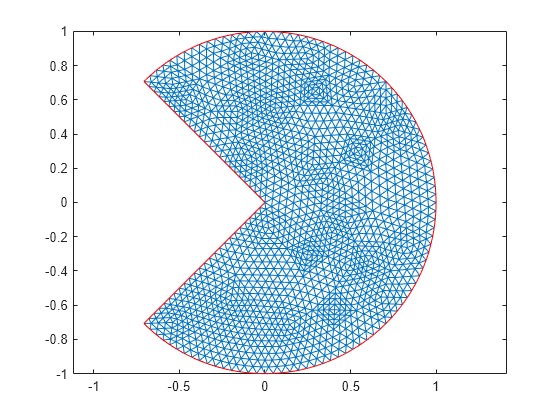
Uniform refinement with more triangles produces a larger error. Typically, a problem with regular solution has an $$O(h^2)$$ error. However, this solution is singular since $$u\approx r^{1/3}$$ at the origin.

Input Arguments

g — Geometry description

decomposed geometry matrix | geometry function | handle to geometry function | AnalyticGeometry object

Geometry description, specified as a decomposed geometry matrix, a geometry function, a handle to the geometry function, or an AnalyticGeometry object. For details about a decomposed geometry matrix, see decsg. For details about a geometry function, see Parameterized Function for 2-D Geometry Creation.

A geometry function must return the same result for the same input arguments in every function call. Thus, it must not contain functions and expressions designed to return a variety of results, such as random number generators.

Data Types: double | char | string | function_handle

b — Boundary conditions

boundary matrix | boundary file | PDEModel object

Boundary conditions, specified as a boundary matrix, boundary file, or a PDEModel object with the boundary condition in its BoundaryConditions property. Pass a boundary file as a function handle or as a file name. Typically, you export a boundary matrix from the PDE Modeler app.

Example: b = 'circleb1', b = "circleb1", or b = @circleb1

Data Types: double | char | string | function_handle

c — PDE coefficient

scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

PDE coefficient, specified as a scalar, matrix, character vector, character array, string scalar, string vector, or coefficient function. c represents the c coefficient in the scalar PDE

$$-\nabla \cdot \left(c\nabla u\right)+au=f$$

or in the system of PDEs

$$-\nabla \cdot \left(c\otimes \nabla u\right)+au=f$$

The coefficients c, a, and f can depend on the solution u if you use the nonlinear solver by setting the value of "Nonlin" to "on". The coefficients cannot be functions of the time t.

Example: "cosh(x+y.^2)"

Data Types: double | char | string | function_handle

a — PDE coefficient

scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

PDE coefficient, specified as a scalar, matrix, character vector, character array, string scalar, string vector, or coefficient function. a represents the a coefficient in the scalar PDE

$$-\nabla \cdot \left(c\nabla u\right)+au=f$$

or in the system of PDEs

$$-\nabla \cdot \left(c\otimes \nabla u\right)+au=f$$

The coefficients c, a, and f can depend on the solution u if you use the nonlinear solver by setting the value of "Nonlin" to "on". The coefficients cannot be functions of the time t.

Example: 2*eye(3)

Data Types: double | char | string | function_handle

f — PDE coefficient

scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

PDE coefficient, specified as a scalar, matrix, character vector, character array, string scalar, string vector, or coefficient function. f represents the f coefficient in the scalar PDE

$$-\nabla \cdot \left(c\nabla u\right)+au=f$$

or in the system of PDEs

$$-\nabla \cdot \left(c\otimes \nabla u\right)+au=f$$

The coefficients c, a, and f can depend on the solution u if you use the nonlinear solver by setting the value of "Nonlin" to "on". The coefficients cannot be function of the time t.

Example: char("sin(x)";"cos(y)";"tan(z)")

Data Types: double | char | string | function_handle

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: [u,p,e,t] = adaptmesh(g,"cirsb",1,0,0,"Maxt",500,"Tripick","pdeadworst","Ngen",50)

Maxt — Maximum number of new triangles

Inf (default) | positive integer

Maximum number of new triangles, specified as a positive integer.

Data Types: double

Ngen — Maximum number of triangle generations

10 (default) | positive integer smaller than intmax

Maximum number of triangle generations, specified as a positive integer smaller than intmax.

Data Types: double

Mesh — Initial mesh

mesh generated by initmesh (default) | [p,e,t] | {p,e,t}

Initial mesh, specified as [p,e,t] or {p,e,t} triples. By default, the function uses the mesh generated by the initmesh function.

Data Types: double

Tripick — Triangle selection method

indices of triangles returned by pdeadworst (default) | MATLAB^® function

Triangle selection method, specified as a MATLAB function. By default, the function uses the indices of triangles returned by the pdeadworst function.

Given the error estimate computed by the function pdejmps, the triangle selection method identifies the triangles to be refined in the next triangle generation. The function is called using the arguments p, t, cc, aa, ff, u, errf, and Par.

• p and t represent the current generation of triangles.

• cc, aa, and ff are the current coefficients for the PDE problem, expanded to the triangle midpoints.

• u is the current solution.

• errf is the computed error estimate.

• Par is the optional argument of adaptmesh.

The matrices cc, aa, ff, and errf all have Nt columns, where Nt is the current number of triangles. The numbers of rows in cc, aa, and ff are exactly the same as the input arguments c, a, and f. errf has one row for each equation in the system. The two standard triangle selection methods are pdeadworst and pdeadgsc.

• pdeadworst identifies triangles where errf exceeds a fraction of the worst value. The default fraction value is 0.5. You can change it by specifying the Par argument value when calling adaptmesh.

• pdeadgsc selects triangles using a relative tolerance criterion.

Data Types: double

Par — Function parameter for triangle selection method

0.5 (default) | number

Function parameter for the triangle selection method, specified as a number between 0 and 1. The pdeadworst triangle selection method uses it as its wlevel argument. The pdeadgsc triangle selection method uses it as its tol argument.

Data Types: double

Rmethod — Triangle refinement method

"longest" (default) | "regular"

Triangle refinement method, specified as "longest" or "regular". For details on the refinement method, see refinemesh.

Data Types: char | string

Nonlin — Toggle to use a nonlinear solver

"off" (default) | "on"

Toggle to use a nonlinear solver, specified as "on" or "off".

Data Types: char | string

Toln — Nonlinear tolerance

1e-4 (default) | positive number

Nonlinear tolerance, specified as a positive number. The function passes this argument to pdenonlin, which iterates until the magnitude of the residual is less than Toln.

Data Types: double

Init — Nonlinear initial value

0 (default) | scalar | vector of characters | vector of numbers

Nonlinear initial value, specified as a scalar, a vector of characters, or a vector of numbers. The function passes this argument to pdenonlin, which uses it as an initial guess in its "U0" argument.

Data Types: double

Jac — Nonlinear Jacobian calculation

"fixed" (default) | "lumped" | "full"

Nonlinear Jacobian calculation, specified as "fixed", "lumped", or "full". The function passes this argument to pdenonlin, which uses it as an initial guess in its "Jacobian" argument.

Data Types: char | string

Norm — Nonlinear solver residual norm

Inf (default) | p value for L^p norm

Nonlinear solver residual norm, specified as p value for L^p norm. p can be any positive real value, Inf, or -Inf. The p norm of a vector v is sum(abs(v)^p)^(1/p). The function passes this argument to pdenonlin, which uses it as an initial guess in its "Norm" argument.

Data Types: double | char | string

MesherVersion — Algorithm for generating initial mesh

"preR2013a" (default) | "R2013a"

Algorithm for generating initial mesh, specified as "R2013a" or "preR2013a". The "R2013a" algorithm runs faster, and can triangulate more geometries than the "preR2013a" algorithm. Both algorithms use Delaunay triangulation.

Data Types: char | string

Output Arguments

u — PDE solution

vector

PDE solution, returned as a vector.

• If the PDE is scalar, meaning that it has only one equation, then u is a column vector representing the solution u at each node in the mesh.

• If the PDE is a system of N > 1 equations, then u is a column vector with N*Np elements, where Np is the number of nodes in the mesh. The first Np elements of u represent the solution of equation 1, the next Np elements represent the solution of equation 2, and so on.

p — Mesh points

2-by-Np matrix

Mesh points, returned as a 2-by-Np matrix. Np is the number of points (nodes) in the mesh. Column k of p consists of the x-coordinate of point k in p(1,k) and the y-coordinate of point k in p(2,k). For details, see Mesh Data as [p,e,t] Triples.

e — Mesh edges

7-by-Ne matrix

Mesh edges, returned as a 7-by-Ne matrix. Ne is the number of edges in the mesh. An edge is a pair of points in p containing a boundary between subdomains, or containing an outer boundary. For details, see Mesh Data as [p,e,t] Triples.

t — Mesh elements

4-by-Nt matrix

Mesh elements, returned as a 4-by-Nt matrix. Nt is the number of triangles in the mesh.

The t(i,k), with i ranging from 1 through end-1, contain indices to the corner points of element k. For details, see Mesh Data as [p,e,t] Triples. The last row, t(end,k), contains the subdomain numbers of the elements.

Algorithms

Mesh Refinement for Improving Solution Accuracy

Partial Differential Equation Toolbox™ provides the refinemesh function for global, uniform mesh refinement for 2-D geometries. It divides each triangle into four similar triangles by creating new corners at the mid-sides, adjusting for curved boundaries. You can assess the accuracy of the numerical solution by comparing results from a sequence of successively refined meshes. If the solution is smooth enough, more accurate results can be obtained by extrapolation.

The solutions of equations often have geometric features such as localized strong gradients. An example of engineering importance in elasticity is the stress concentration occurring at reentrant corners, such as the MATLAB L-shaped membrane. In such cases, it is more efficient to refine the mesh selectively. The selection that is based on estimates of errors in the computed solutions is called adaptive mesh refinement.

The adaptive refinement generates a sequence of solutions on successively finer meshes, at each stage selecting and refining those elements that are judged to contribute most to the error. The process stops34 when the maximum number of elements is exceeded, when each triangle contributes less than a preset tolerance, or when an iteration limit is reached. You can provide an initial mesh, or let adaptmesh call initmesh automatically. You also choose selection and termination criteria parameters. The three components of the algorithm are the error indicator function (computes an estimate of the element error contribution), the mesh refiner (selects and subdivides elements), and the termination criteria.

Error Estimate for FEM Solution

The adaptation is a feedback process. It is easily applied to a larger range of problems than those for which its design was tailored. Estimates, selection criteria, and so on must be optimal for giving the most accurate solution at fixed cost or lowest computational effort for a given accuracy. Such results have been proven only for model problems, but generally, the equidistribution heuristic has been found nearly optimal. Element sizes must be chosen so that each element contributes the same to the error. The theory of adaptive schemes makes use of a priori bounds for solutions in terms of the source function f. For nonelliptic problems, such bounds might not exist, while the refinement scheme is still well defined and works.

The error indicator function used in the software is an elementwise estimate of the contribution, based on [1] and [2]. For Poisson's equation –Δu = f on Ω, the following error estimate for the FEM-solution u_h holds in the L₂-norm $$\Vert \cdot \Vert$$:

$$\Vert \nabla (u-u_h)\Vert \le \alpha \Vert hf\Vert +\beta D_h(u_h)$$

where h = h(x) is the local mesh size, and

$$D_h(v)={\left({\displaystyle \sum _{\tau \in E_1}{h}_{\tau }^2{\left[\frac{\partial v}{\partial n_{\tau }}\right]}^2}\right)}^{1/2}$$

The braced quantity is the jump in normal derivative of v across the edge τ, h_τ is the length of the edge τ, and the sum runs over E_i, the set of all interior edges of the triangulation. The coefficients α and β are independent of the triangulation. This bound is turned into an elementwise error indicator function E(K) for the element K by summing the contributions from its edges.

The general form of the error indicator function for the elliptic equation

–∇ · (c∇u) + au = f

(1)

is

$$E\left(K\right)=\alpha {\Vert h\left(f-au\right)\Vert }_K+\beta {\left(\frac{1}{2}{\displaystyle \sum _{\tau \in \partial K}{h}_{\tau }^2{\left(n_{\tau }·c\nabla u_h\right)}^2}\right)}^{1/2}$$

where $$n_{\tau }$$ is the unit normal of the edge τ and the braced term is the jump in flux across the element edge. The L₂ norm is computed over the element K. The pdejmps function computes this error indicator.

Mesh Refinement Functions

Partial Differential Equation Toolbox mesh refinement is geared to elliptic problems. For reasons of accuracy and ill-conditioning, such problems require the elements not to deviate too much from being equilateral. Thus, even at essentially one-dimensional solution features, such as boundary layers, the refinement technique must guarantee reasonably shaped triangles.

When an element is refined, new nodes appear on its midsides, and if the neighbor triangle is not refined in a similar way, it is said to have hanging nodes. The final triangulation must have no hanging nodes, and they are removed by splitting neighbor triangles. To avoid further deterioration of triangle quality in successive generations, the "longest edge bisection" scheme is used in [3], in which the longest side of a triangle is always split, whenever any of the sides have hanging nodes. This guarantees that no angle is ever smaller than half the smallest angle of the original triangulation.

There are two selection criteria. One, pdeadworst, refines all elements with value of the error indicator larger than half the worst of any element. The other, pdeadgsc, refines all elements with an indicator value exceeding a specified dimensionless tolerance. The comparison with the tolerance is properly scaled with respect to domain, solution size, and so on.

Mesh Refinement Termination Criteria

For smooth solutions, error equidistribution can be achieved by the pdeadgsc selection if the maximum number of elements is large enough. The pdeadworst adaptation only terminates when the maximum number of elements has been exceeded or when the iteration limit is reached. This mode is natural when the solution exhibits singularities. The error indicator of the elements next to the singularity might never vanish, regardless of element size, making equidistribution impossible.

References

[1] Johnson, C. Numerical Solution of Partial Differential Equations by the Finite Element Method. Lund, Sweden: Studentlitteratur, 1987.

[2] Johnson, C., and K. Eriksson. Adaptive Finite Element Methods for Parabolic Problems I: A Linear Model Problem. SIAM J. Numer. Anal, 28, (1991), pp. 43–77.

[3] Rosenberg, I.G., and F. Stenger. A lower bound on the angles of triangles constructed by bisecting the longest side. Mathematics of Computation. Vol 29, Number 10, 1975, pp 390–395.

Version History

Introduced before R2006a

R2013a: Performance and robustness enhancements in meshing algorithm

adaptmesh provides an enhancement option for increased meshing speed and robustness. Choose the enhanced algorithm by setting the MesherVersion name-value pair to 'R2013a'. The default MesherVersion value of 'preR2013a' gives the same mesh as previous toolbox versions.

The enhancement is available inpdeModeler from the Mesh > Parameters > Mesher version menu.