bearingFaultBands
Generate frequency bands around the characteristic fault frequencies of ball or roller bearings for spectral feature extraction
Syntax
Description
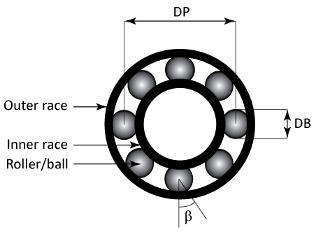
FB = bearingFaultBands(FR,NB,DB,DP,beta)FB of a roller or ball
bearing using its physical parameters. FR is the rotational speed of
the shaft or inner race, NB is the number of balls or rollers,
DB is the ball or roller diameter, DP is the
pitch diameter, and beta is the contact angle in degrees. The values
in FB have the same implicit units as FR.
FB = bearingFaultBands(___,Name,Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
bearingFaultBands computes the different characteristic bearing
frequencies as follows:
Outer race defect frequency,
Inner race defect frequency,
Rolling element (ball) defect frequency,
Cage (train) defect frequency,
References
[1] Chandravanshi, M & Poddar, Surojit. "Ball Bearing Fault Detection Using Vibration Parameters." International Journal of Engineering Research & Technology. 2. 2013.
[2] Singh, Sukhjeet & Kumar, Amit & Kumar, Navin. "Motor Current Signature Analysis for Bearing Fault Detection in Mechanical Systems." Procedia Materials Science. 6. 171–177. 10.1016/j.mspro.2014.07.021. 2014.
[3] Roque, Antonio & Silva, Tiago & Calado, João & Dias, J. "An approach to fault diagnosis of rolling bearings." WSEAS Transactions on Systems and Control. 4. 2009.
Version History
Introduced in R2019b


