interp1
Syntax
Description
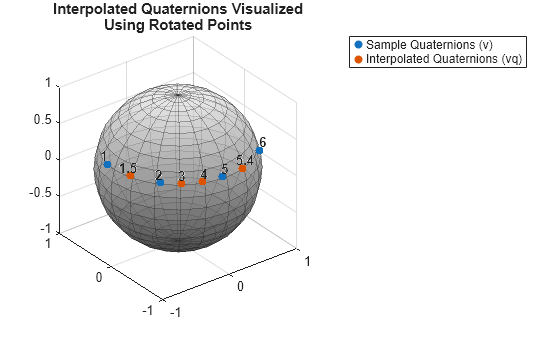
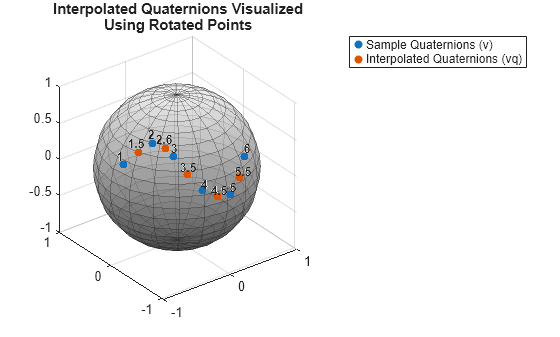
vq = interp1(x,v,xq)x specifies the sample
points, and v specifies the quaternions that contains the
corresponding values v(x). xq specifies the query
points. By default, the function uses "slerp-short" interpolation
method.
vq = interp1(v,xq)v:
When
vis a vector of quaternions, the default points are1:length(v).When
vis an array of quaternions, the default points are1:size(v,1).
Use this syntax when you are not concerned about the absolute distances between sample points.
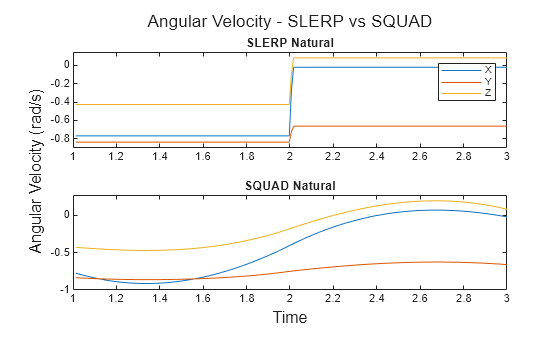
vq = interp1(v,xq,method,extrapolation)
Examples
Input Arguments
Output Arguments
Algorithms
References
[1] Shoemake, Ken. "Animating Rotation with Quaternion Curves." ACM SIGGRAPH Computer Graphics 19, no. 3 (July 1985): 245–54. https://doi.org/10.1145/325165.325242.
[2] Dam, Erik B., Martin Koch, and Martin Lillholm. Quaternions, Interpolation and Animation. Technical Report DIKU-TR-98/5. Department of Computer Science, University of Copenhagen, July 17, 1998. https://web.mit.edu/2.998/www/QuaternionReport1.pdf.
Extended Capabilities
Version History
Introduced in R2025a