barthannwin
Modified Bartlett-Hann window
Description
Examples
Input Arguments
Output Arguments
Algorithms
The equation for computing the coefficients of a Modified Bartlett-Hanning window is
where and the window length is .
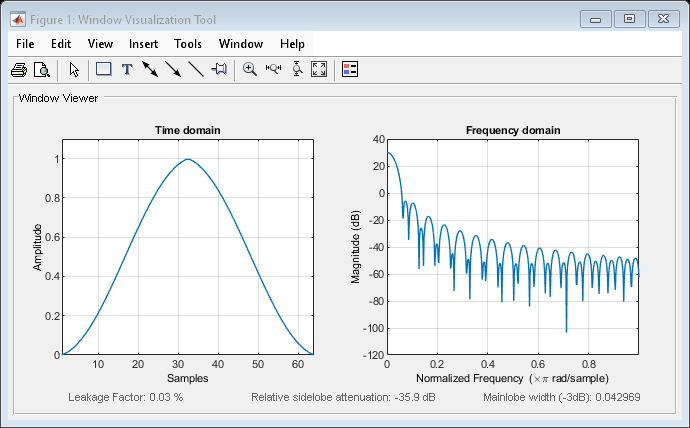
Like Bartlett, Hann, and Hamming windows, this window has a mainlobe at the origin and asymptotically decaying sidelobes on both sides. It is a linear combination of weighted Bartlett and Hann windows with near sidelobes lower than both Bartlett and Hann and with far sidelobes lower than both Bartlett and Hamming windows. The mainlobe width of the modified Bartlett-Hann window is not increased relative to either Bartlett or Hann window mainlobes.
References
[1] Ha, Y. H., and J. A. Pearce. “A New Window and Comparison to Standard Windows.” IEEE® Transactions on Acoustics, Speech, and Signal Processing. Vol. 37, Number 2, 1999, pp. 298–301.
[2] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999, p. 468.
Extended Capabilities
Version History
Introduced before R2006aSee Also
Apps
Functions
bartlett|blackmanharris|bohmanwin|nuttallwin|parzenwin|rectwin|triang| WVTool