Detect Periodicity in a Signal with Missing Samples
Consider the weight of a person as recorded (in pounds) during the leap year 2012. The person did not record their weight every day. You would like to study the periodicity of the signal, even though some data points are missing.
Load the data and convert the measurements to kilograms. Missed readings are set to NaN. Determine how many points are missing.
load('weight2012.dat') wgt = weight2012(:,2)/2.20462; fprintf('Missing %d samples of %d\n',sum(isnan(wgt)),length(wgt))
Missing 27 samples of 366
Determine if the signal is periodic by analyzing it in the frequency domain. The Lomb-Scargle algorithm is designed to handle data with missing samples or data that have been sampled irregularly.
Find the cycle durations, measuring time in weeks.
[p,f] = plomb(wgt,7,'normalized'); plot(f,p) xlabel('Frequency (week^{-1})')
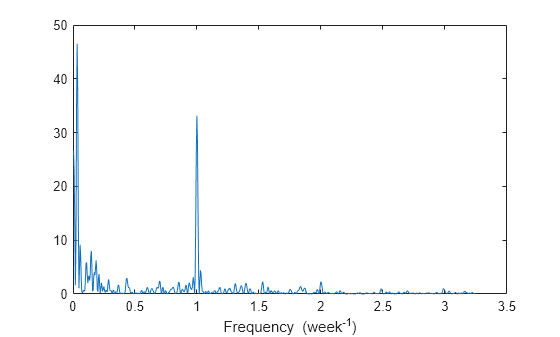
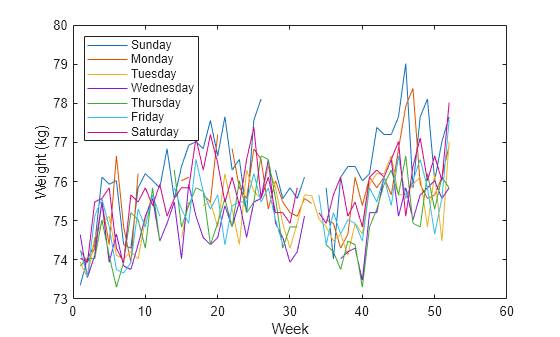
Notice how the person's weight oscillates weekly. Is there a noticeable pattern from week to week? Eliminate the last two days of the year to get 52 weeks. Reorder the measurements according to the day of the week.
wgd = reshape(wgt(1:7*52),[7 52])'; plot(wgd) xlabel('Week') ylabel('Weight (kg)') dweek = datetime([repmat([2012 1],7,1) (1:7)'],'Format','eeee'); legend(string(dweek),'Location','northwest')
Smooth out the fluctuations using a filter that fits low-order polynomials to subsets of the data. Specifically, set it to fit cubic polynomials to sets of seven days.
wgs = sgolayfilt(wgd,3,7); plot(wgs) xlabel('Week') ylabel('Smoothed weight (kg)') legend(string(dweek),'Location','southeast')

This person tends to eat more, and thus weigh more, during the weekend. Verify by computing the daily means. Exclude the missing values from the calculation.
for jk = 1:7 wgm = find(~isnan(wgd(:,jk))); fprintf('%s mean: %5.1f kg\n',dweek(jk),mean(wgd(wgm,jk))) end
Sunday mean: 76.3 kg Monday mean: 75.7 kg Tuesday mean: 75.2 kg Wednesday mean: 74.9 kg Thursday mean: 75.1 kg Friday mean: 75.3 kg Saturday mean: 75.8 kg
See Also
datestr | plomb | sgolayfilt