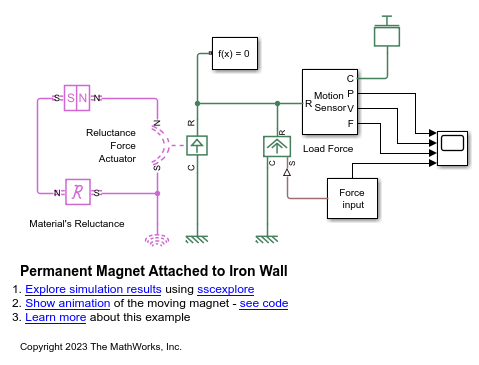
Permanent Magnet
Libraries:
Simscape /
Foundation Library /
Magnetic /
Magnetic Elements
Description
The Permanent Magnet block models a component that passively generates a magnetic field. Use this block to model a magnet that does not magnetize or demagnetize. The magnetic field of the permanent magnet has a magnetic flux density that increases linearly with an increase in the strength of the external magnetic field.
The Permanent Magnet block is equivalent to a Flux Source block and a Reluctance block in parallel or an MMF Source block and a Reluctance block in series. To parameterize the magnet from manufacturer specifications of remanent flux density, magnetic permeability, or coercivity, use the Permanent Magnet block.
Equations
When you subject the Permanent Magnet block to an external magnetic field, the block approximates the flux density B of the resultant magnetic field using one of these linear relationships:
where:
Br is the Remanent flux density of magnet parameter.
μm is the Relative magnetic permeability of material parameter.
μ0 is the magnetic permeability in a vacuum.
H is the strength of the external magnetic field.
Hc is the Coercivity of magnet parameter.
Specify which parameters the block uses to define the linear equation using the Remanent field parametrization parameter.
The linear relationship is valid only when the magnet does not magnetize or demagnetize. The block operates in the second quadrant of the B-H curve:
B ≥ 0
H ≤ 0
The magnetic flux φ flowing through the magnet is defined as:
φ = AB,
where A is the Cross-sectional area parameter.
The magnetomotive force (mmf) across the block is defined as:
MMF = Hl,
where l is the Length of magnet parameter.
The mmf across the block is defined as:
MMF = MMF(N) - MMF(S),
where N and S are the north and south terminals of the permanent magnet, respectively. The flux is positive when the flux flows through the device from the north to the south terminal.
Variables
To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.
Examples
Ports
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2023b