CCCV Battery Charger

Constant-current constant-voltage battery charger

Since R2019a

Description

The CCCV Battery Charger block implements a generic dynamic model battery charger. This model supports three-phase wye or delta AC, one-phase AC, or DC voltage input. The model also provides an optional ambient temperature input for charging voltage temperature compensation.

The figure shows the equivalent circuit for the CCCV Battery Charger block.

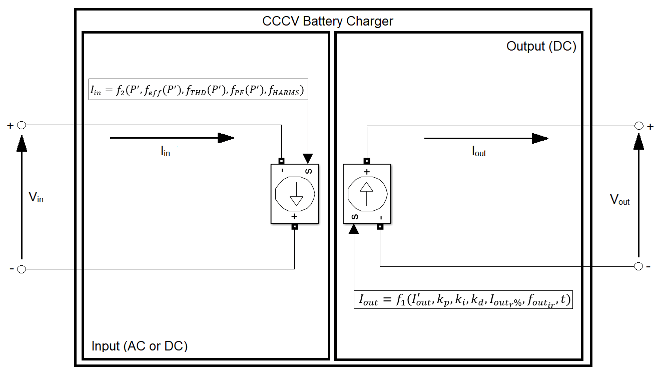
Equations

Output characteristics

The output current of the battery charger is

$I_{out}=f_1(I_{out}^{\text{'}},k_p,k_i,k_d,I_{ou{t}_r\%},f_{ou{t}_{ir}},t)=I_{out}^{\text{'}}\frac{k_i}{k_d{s}^2+k_{p}s+k_i}+\frac{I_{ou{t}_r\%}}{100}\text{sin}(2\pi f_{ou{t}_{ir}}t)$

Variables for the output current and related equations are:

• I_out is the output current command, in A.

• I'_out is the pre-filtered current command, in A.

• k_p is the PID filter proportional gain.

• k_i is the PID filter integral gain.

• k_d is the PID filter differential gain.

• I_outr% is the current output ripple, in %.

• f_outir is the current output ripple frequency, in Hz.

• t is the time, in s.

• ξ is the dampening factor, which is limited to values between 0 and 0.9.

• ⍵_n is the is radian frequency, in rad/s.

• d_% is the overshoot, in %.

• t_s is the settling time, in s.

• I_CC is the pre-filtered current regulated current command, in A.

• I_bulk is the constant current command, in A.

• I_CV is the pre-filtered voltage regulated current command, in A.

• V'_out is the voltage command, in V.

• V'_tc is the voltage command, in V.

• V_out is the temperature compensated voltage effect, in V.

• $\overline{V_{out}}$ is the mean measured output voltage, in V.

• T_a is the ambient temperature, in °C.

• T_nom is the nominal ambient temperature, in °C.

• V_tc is the voltage compensation ratio, in V/°C.

• V_abs is the absorption voltage, in V.

• V_float is the float voltage, in V.

• P is the output power, in W.

• $\overline{I_{out}}$ is the mean measured output current, in A.

The control gains are:

$k_d=1$

$k_p=2\xi {\omega }_n$

$k_i={\omega }_n^2$

The dampening factor is

$\xi =-\frac{\ln \left(\frac{d_{\%}}{100}\right)}{\sqrt{{\pi }^2+\ln {\left(\frac{d_{\%}}{100}\right)}^2}}$

When the output control is current regulated the radian frequency is

${\omega }_n=\frac{-\text{log}(0.02)}{t_s\xi }$

When the output control is voltage regulated the radian frequency is

${\omega }_n=\frac{-\text{log}(0.001)}{\xi }$

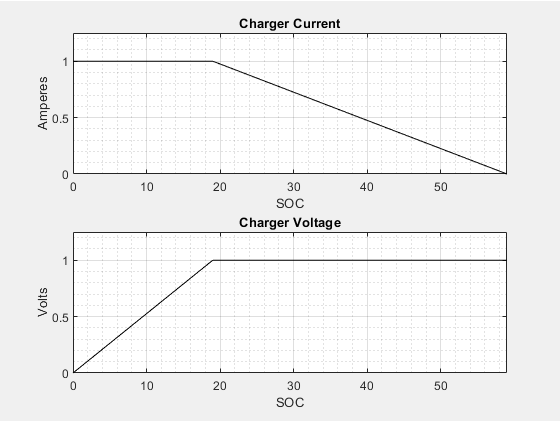
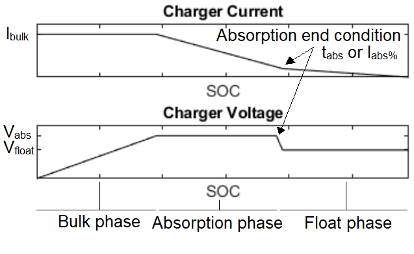
The pre-filtered current command, I'_out, is provided either from the pre-filtered current regulated current command, I_CC, or from the pre-filtered voltage regulated current command, I_CV. The graphs show the different charging cycle phases.

If the Output control mode is set to Constant Current only (CC) or Constant Current - Constant Voltage (CCCV) and V_out is lower than Float voltage or Absorption voltage, while the Absorption end condition isn’t met

$I_{out}^{\text{'}}=I_{CC}=I_{bulk}$

If the Output control mode is set to Constant Current only (CC) or Constant Current - Constant Voltage (CCCV) and V_out is equal to the Float voltage or Absorption voltage, while the Absorption end condition isn’t met

$I_{out}^{\text{'}}=I_{CV}=\frac{(V_{out}^{\text{'}}+V_{tc}^{\text{'}})I_{out}}{\overline{V_{out}}}$

When the Enable absorption phase option is selected and the battery charger switches from constant current to constant voltage control, if the Absorption end condition is not met, the ambient temperature voltage compensation, V'_tc is defined as

$V_{tc}^{\text{'}}=\left(T_a-T_{nom}\right)V_{tc}$

Otherwise, the ambient temperature voltage compensation, V'_tc is defined as

$V_{tc}^{\text{'}}=0$

When the Enable absorption phase option is selected and the battery charger switches from constant current to constant voltage control, if the Absorption end condition is not met, the ambient temperature voltage compensation, V'_out is defined as

$V_{out}^{\text{'}}=V_{abs}$

Otherwise, the ambient temperature voltage compensation, V'_out is defined as

$V_{out}^{\text{'}}=V_{float}$

The output power is defined as

$P=\overline{V_{out}}\overline{I_{out}}$

Input characteristics

The input current of the battery charger is

$I_{in}=f_2(P^{\text{'}},f_{eff}\left(P^{\text{'}}\right),f_{THD}\left(P^{\text{'}}\right),f_{PF}\left(P^{\text{'}}\right),f_{HARMS})$

Variables for the input current and related equations are:

• I_in is the input current command, in A.

• P' is the normalized output power.

• P is the output power, in W.

• P_nom is the nominal output power, in W.

• I'_n is the normalized harmonic amplitude.

• f_in is the input voltage frequency, in Hz.

• f_n is the harmonic frequency, in Hz.

• t is the time, in s.

• V_inA is the input voltage delayed by the fifth of its period, in V.

• V_in is the input voltage of phase A delayed by the fifth of its period, in V.

• I_inr% is the input current ripple, in %.

• f_inir is the input current ripple frequency, in Hz.

• θ_Vin is the input voltage angle, in rad.

• θ_VinA is the input voltage angle of phase A, in rad.

$P^{\text{'}}=\frac{P}{P_{nom}}$

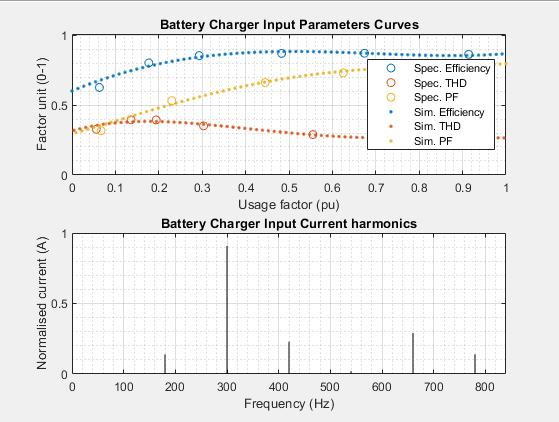
Where, f_eff, is a polynomial function following the parameters Charger efficiency and Efficiency usage factor. This polynomial order is half of the number of data pairs entered. For input values of, P', between 0 and 1, the polynomial must return values between 0 and 1. Otherwise, the polynomial order is reduced until this condition is met. If the order reaches 0, the output will remain constant for the mean value of the dataset.

Where, f_THD, is a polynomial function following the parameters Total harmonic distortion and THD usage factor. This polynomial order is half of the number of data pairs entered. For input values of, P', between 0 and 1, the polynomial must return values between 0 and 1. Otherwise, the polynomial order is reduced until this condition is met. If the order reaches 0, the output will remain constant for the mean value of the dataset.

Where, f_PF, is a polynomial function following the parameters Power factor and PF usage factor. This polynomial order is half of the number of data pairs entered. For input values of, P', between 0 and 1, the polynomial must return values between 0 and 1. Otherwise, the polynomial order is reduced until this condition is met. If the order reaches 0, the output will remain constant for the mean value of the dataset.

Where, f_HARMS, is the sum of sine waves specified with the parameters Harmonics amplitude and Harmonics frequency following the expression

$f_{HARMS}={{\displaystyle \sum }}^{\text{}}{I}_n^{\text{'}}\text{sin}(2\pi f_{in}{f}_{n}t)$

When the Type parameter is set to DC,

$I_{in}=\frac{P^{\text{'}}}{f_{eff}{V}_{in}}+I_{in\_r\%}\text{sin}(2\pi f_{i{n}_{ir}}t)$

When the Type parameter is set to 1-phase AC ,

$I_{in}=\frac{\sqrt{2}{P}^{\text{'}}}{f_{eff}{f}_{PF}{V}_{in}}\left(f_{THD}{f}_{HARMS}+\sin \left({\theta }_{V_{in}}-\text{acos}\left(f_{PF}\right)\right)\right)$

When the Type parameter is set to 3-phase AC (wye) :

$I_{inA}=\frac{\sqrt{2}{P}^{\text{'}}}{3f_{eff}{f}_{PF}{V}_{inA}}\left(f_{THD}{f}_{HARMS}+\sin \left({\theta }_{V_{inA}}-\text{acos}\left(f_{PF}\right)\right)\right)$

$I_{inB}=\frac{\sqrt{2}{P}^{\text{'}}}{3f_{eff}{f}_{PF}{V}_{inA}}\left(f_{THD}{f}_{HARMS}+\sin \left({\theta }_{V_{inA}}-\text{acos}\left(f_{PF}\right)+\frac{1}{3f_{in}}\right)\right)$

$I_{inC}=\frac{\sqrt{2}{P}^{\text{'}}}{3f_{eff}{f}_{PF}{V}_{inA}}\left(f_{THD}{f}_{HARMS}+\sin \left({\theta }_{V_{inA}}-\text{acos}\left(f_{PF}\right)+\frac{2}{3f_{in}}\right)\right)$

When the Type parameter is set to 3-phase AC (delta) :

$I_{inA}=\frac{\sqrt{2}{P}^{\text{'}}}{3f_{eff}{f}_{PF}{V}_{inA}}\left(\frac{1}{3}{f}_{THD}{f}_{HARMS}\text{'}+\frac{1}{\sqrt{3}}\sin \left({\theta }_{V_{inA}}+\frac{\pi }{6}-\text{acos}\left(f_{PF}\right)\right)\right)$

$I_{inB}=\frac{\sqrt{2}{P}^{\text{'}}}{3f_{eff}{f}_{PF}{V}_{inA}}\left(\frac{1}{3}{f}_{THD}{f}_{HARMS}\text{'}\text{'}+\frac{1}{\sqrt{3}}\sin \left({\theta }_{V_{inA}}+\frac{\pi }{6}-\text{acos}\left(f_{PF}\right)+\frac{1}{3f_{in}}\right)\right)$

Where:

$f_{THD}{f}_{HARMS}\text{'}=f_{THD}{f}_{HARMS}\left(\omega t\right)-f_{THD}{f}_{HARMS}\left(\omega t+\frac{1}{3f_{in}}\right)$

$f_{THD}{f}_{HARMS}\text{'}\text{'}=f_{THD}{f}_{HARMS}\left(\omega t+\frac{1}{3f_{in}}\right)-f_{THD}{f}_{HARMS}\left(\omega t+\frac{2}{3f_{in}}\right)$

Assumptions and Limitations

Model Assumptions

• The output load consists of an adequately sized battery.

• Three-phase alternative current inputs are balanced, synchronized, and without jitter.

• The ambient temperature does not affect the charger’s parameters.

Limitations

• The output power is independent from the input power.

Ports

Input

Ta — Ambient temperature

scalar

Ambient temperature supplied to the model. To enable this port, select the Simulate voltage compensation check box.

CC — Constant current

scalar

Signal that defines the current threshold.

This port is visible only when the Dynamic input thresholds parameter is selected, and when the Output control mode parameter is set to Constant Current - Constant Voltage or to Constant Current only.

CV — Constant voltage

vector

Signal that defines the voltage threshold.

This port is visible only when the Dynamic input thresholds parameter is selected, and when the Output control mode parameter is set to Constant Current - Constant Voltage or to Constant Voltage only.

Output

m — Mode

scalar

Simulink^® output of the block specified as a vector containing eight signals. You can demultiplex these signals by using the Bus Selector block from the Simulink library.

Signal	Definition	Units
Input Voltage	The battery charger’s input voltage	V
Input Current	The battery charger’s input current	A
Output Voltage	The battery charger’s output voltage	V
Output Current	The battery charger’s output current	A
Output Ah	The battery charger’s output Ah. The Ah is calculated as: $$Ah=\frac{\overline{I_{out}}{t}_s}{3600}(n)+Ah(n-1)$$	Ah
Output kWh	The battery charger’s output kWh $$kWh=\frac{\overline{V_{out}{I}_{out}}{t}_s}{3600}(n)+Ah(n-1)$$	kWh
Voltage Limit	The battery charger’s output voltage limit	V
Current Limit	The battery charger’s output current limit	A

Conserving

A — a-phase voltage

scalar

A-phase voltage.

B — b-phase voltage

scalar

B-phase voltage.

C — c-phase voltage

scalar

C-phase voltage.

V+ — DC positive voltage

scalar

Positive DC voltage.

V- — DC negative voltage

scalar

Negative DC voltage.

Parameters

General

Preset — Parameterization method

Custom specifications (default) | Primax P4500F-3-125-10 | Transtronic 020-0085-00

The parameter contains a list of two predetermined battery chargers. The parameters in the CCCV Battery Charger block are not enabled when a preset is selected.

Nominal power (W) — Nominal power

1500 (default)

The nominal power, P_nom, of the battery charger in W. The nominal power is used for normalized parameters Charger efficiency, Total harmonic distortion and Power factor. This parameter must be greater than or equal to the product of Bulk current and Float voltage or Absorption voltage if Enable absorption phase is selected.

Input

Type — Input voltage type

3-phases AC (wye) (default) | 3-phases AC (delta) | 1-phase AC | DC

Input voltage type:

• 3-phases AC (wye) — The A, B, and C ports become visible to supply the balanced three-phase alternating current power.

• 3-phases AC (delta) — The A, B, and C ports become visible to supply the balanced three-phase alternating current power.

• 1-phases AC — The A and B ports become visible to supply the balanced single-phase alternating current power.

• DC — The + and - ports become visible to supply the direct current power.

External neutral connection — Neutral connection option

cleared (default) | selected

Option to enable access to a neutral connection externally through the N port. Otherwise, the neutral is internally connected.

Dependencies

This option is enabled when the Type is set to 3-phases AC (wye).

Effective voltage (V) — Effective voltage

208 (default)

Effective voltage, V_eff, of the battery charger power input in V. When Type is either 3-phases AC (wye) or 3-phases AC (delta), the effective voltage must the rms line voltage.

Frequency (Hz) — Frequency

60 (default)

Frequency, f_in, of the battery charger power input in Hz.

Dependencies

This parameter is accessible when Type is set to 3-phases AC (wye), 3-phases AC (delta), or 1-phase AC.

Current ripple (%) — Current ripple

10 (default)

Current ripple, I(_inr%), of the battery charger input current.

Dependencies

This parameter is accessible when Type is set to DC (wye).

Ripple frequency (Hz) — Ripple frequency

1000 (default)

Ripple frequency of the battery charger input current.

Dependencies

This parameter is accessible when Type is set to DC (wye).

Plot Curves — Click to plot input parameter and input current harmonics curves for the battery charger.

Simulate efficiency — Efficiency simulation option

cleared (default) | selected

Option to simulate efficiency.

Dependencies

When this parameter is selected, the parameters Charger efficiency and Efficiency usage factor become visible. Otherwise, the battery charger efficiency factor is set to a constant value of 1.

Charger efficiency [0-1] — Battery charger efficiency factor

[0.627 0.803 0.855 0.871 0.872 0.864] (default)

Efficiency factor, η_y, of the battery charger. This parameter is used with the Efficiency usage factor to approximate a polynomial function corresponding to the full operation range efficiency normalized on the Nominal Power.

Efficiency usage factor (pu) — Battery charger efficiency usage factor

[0.063 0.177 0.293 0.483 0.674 0.914] (default)

Efficiency usage factor of the battery charger. This parameter is used with the Charger efficiency to approximate a polynomial function corresponding to the full operation range efficiency normalized on the Nominal Power.

Simulate THD — THD simulation option

cleared (default) | selected

Total harmonic distortion (THD) simulation option.

Dependencies

When this parameter is selected, the parameters Total harmonic distortion, THD usage factor, Harmonics amplitude, and Harmonics frequency become visible. Otherwise, the battery charger THD factor is set to a constant value of 0.

Total harmonic distortion [0-1] — THD

[0.327 0.394 0.394 0.351 0.289 0.265] (default)

The total harmonic distortion factor, THD_y, of the battery charger. This parameter is used with the THD usage factor (pu) to approximate a polynomial function corresponding to the full operation range THD normalized on the Nominal Power.

THD usage factor (pu) — THD usage factor

[0.056 0.136 0.194 0.303 0.555 0.916] (default)

The total harmonic distortion usage factor, THD_y, of the battery charger. This parameter is used with the Total harmonic distortion [0-1] to approximate a polynomial function corresponding to the full operation range THD normalized on the Nominal Power.

Harmonics amplitude (A) — Harmonic amplitude

[0.199 1.297 0.328 0.029 0.416 0.200] (default)

Harmonics amplitude, I_n, of the battery charger input current in A. This parameter is used with the Harmonics frequency to generate the battery charger’s input current harmonics signature. The harmonics amplitude parameter’s values are normalized to 1 using this:

$I_n^{\text{'}}=\frac{I_n}{\sqrt{{{\displaystyle \sum }}^{\text{}}{I}_n^2}}$

Dependencies

This parameter is accessible when the Type is set to 3-phases AC (wye), 3-phases AC (delta), or 1-phase AC.

Harmonics frequency (n) — Harmonic frequency

[3 5 7 9 11 13] (default)

The harmonics frequency, f_n, of the battery charger’s input current in n multiples of Frequency. This parameter is used with the Harmonics amplitude to generate the battery charger’s input current harmonics signature.

Dependencies

This parameter is accessible when the Type is either 3-phases AC (wye), 3-phases AC (delta), or 1-phase AC.

Simulate power factor — Power factor simulation option

cleared (default) | selected

Option to simulate power factor. Otherwise, the battery charger’s PF is set to a constant equal to 1.

Dependencies

This parameter is accessible when the Type is set to 3-phases AC (wye), 3-phases AC (delta), or 1-phase AC. When this parameter is selected, the parameters Power factor and PF usage factor become visible.

Power factor [0-1] — Power factor

[0.316 0.532 0.662 0.731 0.780 0.792] (default)

Total harmonic distortion factor, or power factor, PF_y, of the battery charger. This parameter is used with the PF usage factor to approximate a polynomial function corresponding to the full operation range’s PF normalized on the Nominal Power.

Dependencies

This parameter is accessible when the Type is set to 3-phases AC (wye), 3-phases AC (delta), or 1-phase AC.

PF usage factor (pu) — Power factor usage factor

[0.067 0.230 0.445 0.625 0.794 0.919] (default)

The PF usage factor, PF_y, of the battery charger. This parameter is used with the Power factor to approximate a polynomial function corresponding to the full operation range PF normalized on the Nominal Power

Charging Mode

Output control mode — Output control method

Constant Current - Constant Voltage (CCCV) (default) | Constant Current only (CC) | Constant Voltage only (CV)

Methods for output control are:

• Constant Current - Constant Voltage (CCCV) — This charging mode regulates the output current and voltage.

• Constant Current only (CC) — This charging mode regulates the output current.

• Constant Voltage only (CV) — This charging mode regulates the output voltage.

Dependencies

Different options expose different parameters.

Dynamic input thresholds — Dynamic input thresholds option

selected (default) | cleared

Option to enable dynamic access to the output current and voltage thresholds. Otherwise, these thresholds are set withBulk current and Float voltage or Absorption voltage.

Dependencies

The CC or CV input ports become visible to supply the current and voltage thresholds depending on the Output control mode selected.

Bulk current (A) — Bulk current

10 (default)

The bulk current, I_bulk, of the battery charger maximum output current in A. While the output voltage is lower than Float voltage or Absorption voltage, the battery charger limits the output current to maintain a constant current.

Dependencies

This parameter is accessible when the Output control mode is either Constant Current - Constant Voltage (CCCV) or Constant Current only (CC).

Float voltage (V) — Float voltage

138 (default)

Float voltage, V_float, of the battery charger steady-state output voltage in V. When the output voltage reaches this value, the battery charger reduces the output current to maintain a constant voltage.

Dependencies

This parameter is accessible when the Output control modeis either Constant Current - Constant Voltage (CCCV) or Constant Voltage only (CV).

Enable absorption phase — Absorption phase option

cleared (default) | selected

Option to enable the battery charging absorption phase. The charging phase allows the battery charger to maintain a higher Absorption voltage than Float voltage for a specified Absorption end condition when switching from constant current to constant voltage charging.

Dependencies

This parameter is accessible when the Output control mode is Constant Current - Constant Voltage (CCCV) and the Dynamic input thresholds is cleared.

Absorption voltage (V) — Absorption voltage

142 (default)

Absorption voltage, V_abs, of the battery charger transition voltage when switching from constant current to constant voltage charging. The battery charger’s absorption voltage will be maintained while the Absorption end condition isn’t met. This parameter must be greater than the float voltage.

Dependencies

This parameter is accessible when the Enable absorption phase is selected.

Absorption end condition — Absorption end condition

Time based (default) | Current based

Choose between two absorption end conditions:

• Time based — This end condition requires a specified Absorption time while maintaining the Absorption voltage before lowering the battery charger’s output voltage to Float voltage.

• Current based — This end condition requires a specified Absorption current while maintaining the Absorption voltage before lowering the battery charger’s output voltage to Float voltage.

Dependencies

This parameter is accessible when Enable absorption phase is selected.

Absorption time (s) — Absorption time

3600 (default)

Absorption time, t_abs, of the time-based end condition of the absorption phase in s. When the Absorption voltage has been maintained for the specified time, the output voltage is lowered to the Float voltage.

Dependencies

This parameter is accessible when the Absorption end condition is Time based.

Absorption current (%) — Absorption current

40 (default)

Absorption current, I_abs%, of the absorption phase’s current-based end condition in %. When the output current reaches the specified percentage of the Bulk current, the output voltage lowers from the Absorption voltage to the Float voltage. This parameter is accessible when the Absorption end condition is Current based.

Dependencies

This parameter is accessible when the Absorption end condition is Current based.

Plot Curves — Click to plot input parameter and input current harmonics curves for the battery charger.

Output

Current ripple (%) — Current ripple

0.5 (default)

The output ripple, I_outr%, of the battery charger current specified as a %.

Ripple frequency (Hz) — Ripple frequency

1000 (default)

f_outir

Ripple frequency, f_outir, of the battery charger output current in Hz.

Overshoot (%) — System overshoot

1 (default)

The overshoot, d_%, of the battery charger’s output control dynamic in %. This parameter is applied to the Bulk current, Float voltage and Absorption voltage depending on charging phase.

Settling time (s) — System settling time

5 (default)

Settling time, t_s, at which the battery charger’s output control dynamic reaches 2% of its steady-state value in s. This parameter is applied to the Bulk current, Float voltage and Absorption voltage depending on charging phase.

Dependencies

Simulate voltage compensation — Voltage compensation option

cleared (default) | selected

Option to enable output voltage temperature compensation. When enabled, the Float voltage and Absorption voltage will vary depending on the ambient temperature, Voltage compensation and Nominal temperature.

Voltage compensation (V/deg. C) — Voltage compensation

-0.18 (default)

Voltage compensation, V_tc, of the battery charger output in V/°C.

Dependencies

This parameter is accessible when the Simulate voltage compensation is selected.

Nominal temperature (deg. C) — Nominal temperature

20 (default)

Nominal temperature, T_nom, of the required battery float voltage in °C.

Dependencies

This parameter is accessible when the Simulate voltage compensation is selected.

References

[1] Cope, R.C., and Y. Podrazhansky. The Art of Battery Charging. Proc. 14th Annual Battery Conference on Applications and Advances, pp. 233-235. Long Beach, CA: 1999.

[2] Dubey, A., Santoso, S., and M.P. Cloud. Average-Value Model of Electric Vehicle Chargers. IEEE Transactions on Smart Grid Vol. 4 No. 3. Pp. 1549-1557. Argonne, IL: IEEE Power & Energy Society, 2013.

[3] Elias, M., Nor, K., and A. Arof. Design of Smart Charger for Series Lithium-Ion Batteries. Proceedings from IEEE International Conference on Power Electronics and Drive Systems, pp. 1485-1490. Kuala Lumpur: PEDS, 2005.

[4] Hussein A.A.-H., and I. Batarseh. A Review of Charging Algorithms for Nickel and Lithium Battery Chargers. IEEE Transactions on Vehicular Technology. Sendai, Japan: IEEE Vehicular Technology Society, 2011.

Version History

Introduced in R2019a