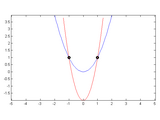
Conics intersection
The homogeneous representation of a conic is a matrix
m = [A C D; C B E; D E F] that represents the equation
A x^2 + B y^2 + 2C xy + 2D x + 2Ey + F = 0
Given two matrix E1 and E2 representing two conics, the code will detect all their intersections.
For instance:
___________________
%a circle centered in the origin
E1 = [1 0 0; 0 1 0; 0 0 -3]
%an ellipse centered in the origin
E2 = [1 0 0; 0 3 0; 0 0 -6]
%get the four homogeneous intersections
P = intersectConics(E1, E2)
%plot the normalized points
plot(P(1,:) ./ P(3,:) , P(2,:) ./ P(3,:), 'ro');
___________________
For more info: http://www.pigei.com/conics-intersection
and a detailed example describing the method: http://math.stackexchange.com/questions/316849/intersection-of-conics-using-matrix-representation
A C++ open souce implementation is also present at https://bitbucket.org/pierluigi/conicsintersection
___________________
If this code was useful, please consider a donation:
Bitcoin: 3BUD7cEnbpp15hZXbPZpdgnH11FAV1kvfi
Cita come
Pierluigi Taddei (2026). Conics intersection (https://it.mathworks.com/matlabcentral/fileexchange/28318-conics-intersection), MATLAB Central File Exchange. Recuperato .
Compatibilità della release di MATLAB
Compatibilità della piattaforma
Windows macOS LinuxCategorie
Tag
Scopri Live Editor
Crea script con codice, output e testo formattato in un unico documento eseguibile.