Marginal distributions of a bivariate function
function [fx, fy, MeanVar] = marginaldist(f,x,y,distributionType)
f is a bivariate function, which can be a normalized or unnormalized distribution function. x and y are the two independent variables of f. The variable values can be taken as either row or column vectors. fx and fy are the marginal distributions of x and y, respectively.
distributionType defines whether the marginal distributions have to be computed on continuous or discrete domain. Default is continuous. The strings that can be assigned to distributionType as an input may include:
(for continuous) 'Continuous','continuous','Con', or 'con'
and (for discrete) 'Discrete','discrete','Dis', or 'dis'
MeanVar is optional. This is a vector output, whose elements are mean of fx, variance of fx, mean of fy, and variance of fy, respectively.
Define function f in a separate m-file. In the example below, we take a two-dimensional Gaussian function as our test function, whose m-file is saved as testFunction.m
function f = testFunction(x,y)
sx = 2; sy = 0.5; mx = 2; my = -1; % s stands for variance, and m for mean
f = 1/(2*pi*sx*sy)*exp(-(x-mx).^2/(2*sx^2)-(y-my).^2/(2*sy^2));
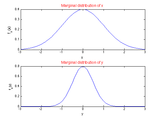
Example 1
x = -10:0.1:10; y = -10:0.1:10;
[fx, fy, MV] = marginaldist(@testFunction,x,y,'continuous');
subplot(211), plot(x,fx), xlabel('x'), ylabel('f_x(x)')
title('Marginal distribution of x','FontSize',12,'Color','r')
subplot(212), plot(y,fy), xlabel('y'), ylabel('f_y(y)')
title('Marginal distribution of y','FontSize',12,'Color','r')
Example 2
x = -10:10; y = -10:10;
[fx, fy] = marginaldist(@testFunction,x,y,'discrete');
subplot(211), plot(x,fx), xlabel('x'), ylabel('f_x(x)')
title('Marginal distribution of x','FontSize',12,'Color','r')
subplot(212), plot(y,fy), xlabel('y'), ylabel('f_y(y)')
title('Marginal distribution of y','FontSize',12,'Color','r')
Cita come
Shoaibur Rahman (2024). Marginal distributions of a bivariate function (https://www.mathworks.com/matlabcentral/fileexchange/48770-marginal-distributions-of-a-bivariate-function), MATLAB Central File Exchange. Recuperato .
Compatibilità della release di MATLAB
Compatibilità della piattaforma
Windows macOS LinuxCategorie
Tag
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Scopri Live Editor
Crea script con codice, output e testo formattato in un unico documento eseguibile.
MarginalDistribution/
| Versione | Pubblicato | Note della release | |
|---|---|---|---|
| 1.4.0.0 | This revised version includes the flexibility of getting means and variances of two marginal distributions computed. |
||
| 1.3.0.0 | includes test function m-file |
||
| 1.2.0.0 | Image File |
||
| 1.1.0.0 | Title modification on 16/12/2014 |
||
| 1.0.0.0 |