multitone

Generate sparse multitone signal

Since R2025a

Syntax

mtone = multitone(fs)

mtone = multitone(fs,Name=Value)

[mtone,mtoneinfo] = multitone(___)

multitone(___)

Description

mtone = multitone(fs) returns a test audio signal with a mix of sinusoids. By default, the multitone signal conforms to the IEC 60268-21 standard [2]. For an example that uses a multitone test signal to excite a system and analyzes the response, see Audio Device Test Stimuli.

mtone = multitone(fs,Name=Value) specifies options using one or more name-value arguments.

[mtone,mtoneinfo] = multitone(___) also returns a struct with information describing the creation of the test signal. This information is useful when analyzing the response of a system excited by the multitone signal.

multitone(___) with no output arguments plots the generated multitone signal in the frequency domain.

Examples

Generate Multitone Test Signal

Use multitone to generate a default multitone test signal with a sample rate of 48,000 Hz.

fs = 48e3;
mtone = multitone(fs);

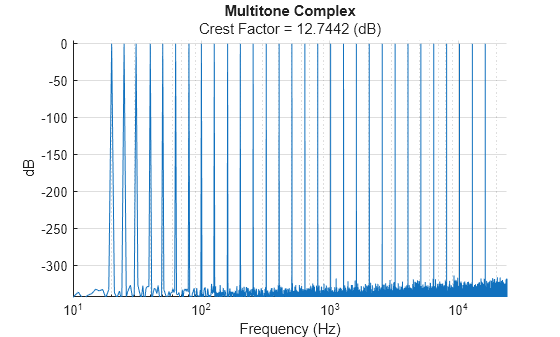
Call multitone with no output arguments to view the generated signal in the frequency domain.

multitone(fs)

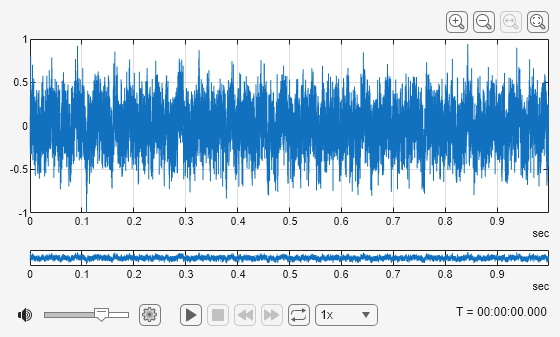
Use audioViewer to view and listen to the multitone signal.

audioViewer(mtone,fs)

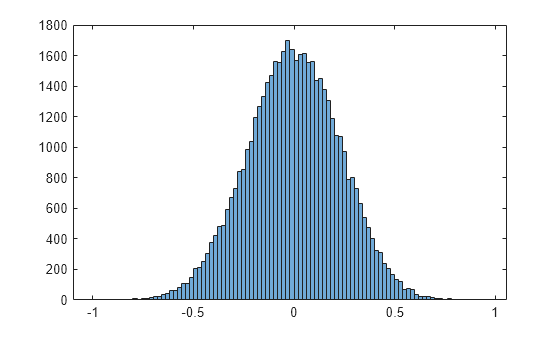
View a histogram of the multitone signal. The distribution approaches Gaussian, which is a good approximation to musical signals when exercising loudspeakers.

histogram(mtone)

Calculate the crest factor of the generated signal. On average, musical signals have a crest factor approaching 12 dB.

20*log10(peak2rms(mtone))

ans = 
12.7442

Control Placement of Tones in Multitone Signal

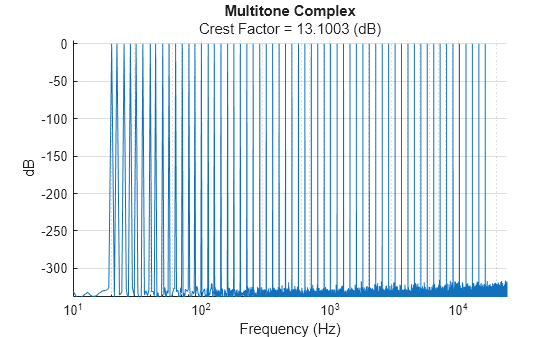
By default, the multitone function places tones in the frequency domain according to the IEC 60268-21 standard. You can use the RelativeResolution and FrequencyRange arguments to modify the tone placement according to IEC 60268-21. Set RelativeResolution to place six tones per octave. Set FrequencyRange to place tones on a range from 20 Hz to 18,000 Hz. The ExcitationTime argument also has an effect on the frequency bin placement because it controls the number of points in the DFT.

fs = 48e3;
multitone(fs, ...
    ExcitationTime=1, ...
    RelativeResolution=6, ...
    FrequencyRange=[20,18000])

The multitone function places tones per octave by default, as specified in IEC 60268-21. However, you can alternatively specify the number of tones in each decade by setting ToneSpacing to "decade", for ${\log }_{10}$ spacing.

multitone(fs, ...
    ToneSpacing="decade", ...
    RelativeResolution=6, ...
    FrequencyRange=[20,18000])

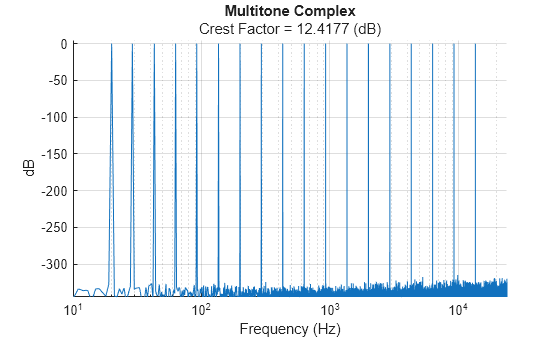
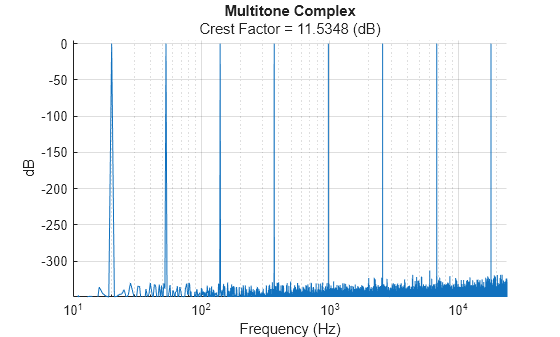
Alternatively, you can specify the total number of tones in the signal, spaced in the linear or log domain.

multitone(fs, ...
    ToneSpacing="log", ...
    NumTones=8, ...
    FrequencyRange=[20,18000])

Adjust Crest Factor of Multitone Signal

You can call multitone with the TargetCrestFactor argument to design a test signal with the desired crest factor. The function searches through the space of parameters of the phase algorithm and returns the signal with the closest crest factor to the target.

fs = 48e3;
mtone = multitone(fs,TargetCrestFactor=10);
crestFactor = 20*log10(peak2rms(mtone))

crestFactor = 
11.4791

With the default multitone arguments, you cannot adjust the crest factor of the resulting signal very much. See how setting the TargetCrestFactor to the minimum of zero and the maximum of 30 only adjusts the crest factor by plus or minus one dB.

mtone = multitone(fs,TargetCrestFactor=0);
crestFactor = 20*log10(peak2rms(mtone))

crestFactor = 
11.4791

mtone = multitone(fs,TargetCrestFactor=30);
crestFactor = 20*log10(peak2rms(mtone))

crestFactor = 
13.9114

However, using linearly-spaced tones can improve your ability to adjust the crest factor. See how the crest factor range increases when you set ToneSpacing to "linear".

mtone = multitone(fs,ToneSpacing="linear",TargetCrestFactor=0);
crestFactor = 20*log10(peak2rms(mtone))

crestFactor = 
7.2033

mtone = multitone(fs,ToneSpacing="linear",TargetCrestFactor=30);
crestFactor = 20*log10(peak2rms(mtone))

crestFactor = 
12.2133

Combining the Newman phase algorithm with linearly-spaced tones can further improve your ability to adjust the crest factor.

mtone = multitone(fs,ToneSpacing="linear", ...
    PhaseAlgorithm="newman",TargetCrestFactor=0);
crestFactor = 20*log10(peak2rms(mtone))

crestFactor = 
5.4646

mtone = multitone(fs,ToneSpacing="linear", ...
    PhaseAlgorithm="newman",TargetCrestFactor=30);
crestFactor = 20*log10(peak2rms(mtone))

crestFactor = 
13.6428

Generate Multitone Test Signal with Pre-Excitation and Multiple Runs

It is often necessary to warm up a system under test with a pre-excitation before playing the test signal. The IEC 60268-21 standard suggests a pre-excitation signal with a length between $$T/2$$ and $$T$$, where $$T$$ is the length of the multitone test signal. Additionally, IEC 60268-21 suggests repeating the multitone test stimulus multiple times for statistical averaging of the responses. Finally, it is advisable to insert a pause between runs of the test signal to avoid over heating the system.

Use multitone to create a test signal with a pre-excitation time of 0.75 seconds, an excitation time of one second, three separate runs, and a pause between runs of five seconds.

fs = 48e3;
[mtone,xinfo] = multitone(fs, ...
    PreExcitationTime=0.75, ...
    ExcitationTime=1, ...
    PauseTime=5, ...
    NumRuns=3);

Get the timing information from the struct describing the creation of the test signal.

preExcitationSamples = xinfo.Duration.PreExcitationTime*fs;
excitationSamples = xinfo.Duration.ExcitationTime*fs;
pauseSamples = xinfo.Duration.PauseTime*fs;
oneRunSamples = preExcitationSamples + excitationSamples + pauseSamples;
numRuns = xinfo.Duration.NumRuns;

Use the timing information to segment the multitone signal into the pre-excitation, excitation, and pause stages.

preExcitationMask = sigroi2binmask([1,preExcitationSamples],oneRunSamples);
preExcitationMask = repmat(preExcitationMask,numRuns,1);
preExcitationMask = preExcitationMask(1:end-pauseSamples); % Remove final pause
preExcitation = mtone;
preExcitation(~preExcitationMask) = nan;

excitationROI = [preExcitationSamples+1,preExcitationSamples+excitationSamples];
excitationMask = sigroi2binmask(excitationROI,oneRunSamples);
excitationMask = repmat(excitationMask,numRuns,1);
excitationMask = excitationMask(1:end-pauseSamples); % Remove final pause
excitation = mtone;
excitation(~excitationMask) = nan;

pauseSegment = mtone;
pauseSegment(preExcitationMask | excitationMask) = nan;

Plot the segmented multitone signal with its pre-excitation and multiple runs.

tvec = (0:(numel(mtone)-1))/fs;
plot(tvec,preExcitation,tvec,excitation,tvec,pauseSegment)
xlabel("Time (s)")
legend("Pre-Excitation","Excitation","Pause")

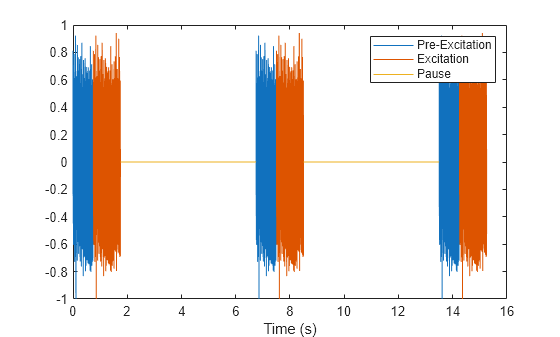
Input Arguments

fs — Sample rate (Hz)

positive scalar

Sample rate of generated multitone signal in Hertz.

Data Types: single | double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: mtone = multitone(48e3,ToneSpacing="linear")

FrequencyRange — Frequency range (Hz)

[20, floor(0.4*fs)] (default) | two-element row vector

Frequency range over which to place the tones, in Hz, specified as a two-element monotonically increasing row vector in the range [1, fs/2].

Data Types: single | double

ToneSpacing — Tone spacing method

"octave" (default) | "linear" | "decade" | "log"

Tone spacing method, specified as "linear", "decade", "octave", or "log".

If you specify RelativeResolution, ToneSpacing defaults to "octave". If you specify NumTones, ToneSpacing defaults to "log". If you specify neither NumTones nor RelativeResolution, ToneSpacing defaults to "octave".

If you specify ToneSpacing as "decade" or "octave", use the RelativeResolution argument to specify the number of tones in each interval. If you specify ToneSpacing as "linear" or "log", use the NumTones argument to specify the total number of tones distributed uniformly in the requested domain.

Data Types: char | string

NumTones — Total number of tones

12 (default) | integer greater than 1

Number of tones within the FrequencyRange, specified as an integer greater than 1. This argument applies only when ToneSpacing is "linear" or "log".

Data Types: single | double

RelativeResolution — Number of tones within each interval

3 (default) | integer in the range [1,48]

Number of tones within each octave or decade, specified as an integer in the range [1,48]. This argument applies only when ToneSpacing is "octave" or "decade".

Data Types: single | double

ShapingCurve — Spectrum-shaping curve

"white" (default) | "pink" | "IEC 60268-21" | two-column matrix

Spectrum-shaping curve applied to the multitone signal, specified as "white", "pink", "IEC 60268-21", or a two-column matrix. If you specify a two-column matrix, the first column is a frequency in Hz and the second column is a level in dB. If the matrix grid does not map to the spectrum, the function linearly interpolates the values.

If you specify ShapingCurve as "white", no shaping is applied to the spectrum of the multitone signal. If you specify ShapingCurve as "pink", the function applies a pink-noise-shaped curve to the spectrum of the signal, where the power spectral density is inversely proportional to the frequency. If you specify ShapingCurve as "IEC 60268-21", the function applies the spectrum-shaping curve suggested in IEC 60268-21.

Data Types: char | string | single | double

TargetCrestFactor — Target crest factor (dB)

scalar in the range [0,30]

Target crest factor in dB, specified as a scalar in the range [0,30]. The crest factor of a signal is the ratio of the peak magnitude of the signal to the root-mean-square (RMS) value of the signal. It is generally desirable for your test signal to have a crest factor similar to that of the signals expected to be played on the device under test.

If you specify this argument, the function attempts to reach the target crest factor by sweeping through the parameters of the PhaseAlgorithm. If PhaseAlgorithm is "newman", the function additionally applies the algorithm in [4] to reach the target crest factor. If you do not specify TargetCrestFactor, the function initializes the phase values according to the PhaseAlgorithm defaults.

Data Types: single | double

PhaseAlgorithm — Phase algorithm

"IEC 60268-21" (default) | "newman"

Phase algorithm, specified as "newman" or "IEC 60268-21". Set this argument to "IEC 60268-21" to design the signal with pseudorandom phases according to the IEC 60268-21 standard [2]. Set this argument to "newman" to design the signal phase according to the algorithm described in [1] and [3].

Data Types: char | string

ExcitationTime — Multitone excitation time (s)

1 (default) | positive scalar

Multitone excitation time in seconds, specified as a positive scalar.

Data Types: single | double

PreExcitationTime — Pre-excitation time (s)

0 (default) | nonnegative scalar

Pre-excitation time in seconds, specified as a nonnegative scalar.

Data Types: single | double

PauseTime — Pause time between runs (s)

0 (default) | nonnegative scalar

Pause time between runs in seconds, specified as a nonnegative scalar.

Data Types: single | double

NumRuns — Number of runs

1 (default) | positive integer

Number of excitation runs, specified as a positive integer. Multiple runs repeats the excitation signal for statistical averaging.

Data Types: single | double

Output Arguments

mtone — Multitone signal

column vector

Multitone signal, returned as a column vector representing the time-domain signal. The function scales the signal such that its maximum value is one.

Data Types: double

mtoneinfo — Signal information

struct

Information about the generated signal, returned as a struct with the following fields:

• SampleRate — Sample rate in Hz.

• NumDFTPoints — Number of points in DFT.

• Tones — Information about the tones, returned as a struct with the following fields:

  • RelativeResolution — Number of tones within each interval. This field is present only when the ToneSpacing argument is "octave" or "decade".

  • Bin — Vector of bin indices corresponding to tones given the DFT of the signal.

  • Frequency — Vector of tone frequencies in Hz.

  • Magnitude — Vector of relative magnitudes of tones in dB.

  • Phase — Vector of tone phases in the range [-π,π].

  • PhasesParameters — Parameters used to determine the phase, returned as a struct with the field Name containing the name of the phase algorithm. The remaining fields in the PhaseParameters struct depend on the phase algorithm:

    • If PhaseAlgorithm is "IEC 60268-21", then the struct has fields m, c, a, and n0. These parameters define the phase construction according to the algorithm described in IEC 60268-21.

    • If PhaseAlgorithm is "newman", then the struct has the field C, which is a multiplier on the standard Newman algorithm that can be adjusted to reach a target crest factor.

• ShapingCurve — Spectral shaping curve.

• Duration — Information about the duration of the signal, returned as a struct with the following fields:

  • PreExcitationTime — Time before excitation signal begins, in seconds.

  • ExcitationTime — Duration of the excitation signal in seconds.

  • PauseTime — Pause between excitation runs, in seconds.

  • NumRuns — Number of excitation runs.

  • TotalTime — Total time of the signal, including repeated excitations, in seconds.

• Kurtosis — Kurtosis of the signal.

• CrestFactor — Crest factor of the signal in dB.

References

[1] Boyd, S. “Multitone Signals with Low Crest Factor.” IEEE Transactions on Circuits and Systems 33, no. 10 (October 1986): 1018–22. https://doi.org/10.1109/TCS.1986.1085837.

[2] IEC 60268-21:2018. "Sound system equipment - Part 21: Acoustical (output-based) measurements." International Electrotechnical Commission.

[3] Newman, D. J. "An L1 Extremal Problem for Polynomials." Proceedings of the American Mathematical Society 16, no. 6 (1965): 1287-1291.

[4] Yang, Yuxiang, Fu Zhang, Kun Tao, Benjamin Sanchez, He Wen, and Zhaosheng Teng. “An Improved Crest Factor Minimization Algorithm to Synthesize Multisines with Arbitrary Spectrum.” Physiological Measurement 36, no. 5 (May 1, 2015): 895–910. https://doi.org/10.1088/0967-3334/36/5/895.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2025a