Ambisonic Spatial Transformations

Introduction

In this example, you learn how to apply spatial transformations to an ambisonic signal. Specifically, you apply the following effects:

• Mirroring against the three cartesian axes.

• 3D rotation (roll, pitch and yaw).

You apply the effect by computing a transformation matrix, T, and applying it when you decode the signal.

The decoded ambisonic signal can be expressed as:

$\mathit{Y}=\mathit{X}.\mathit{T}.\mathit{D}$, where:

• X is the M-by-N ambisonic encoded signal, where M is the signal length, $\mathit{N}={\left(1+\mathrm{order}\right)}^2$, and order is the ambisonic order.

• D is the N-by-L ambisonic decoder matrix, where L is the number of loudspeakers.

• T is the N-by-N transformation matrix, which depends on the applied effect.

Mirroring

Mirroring an ambisonic signal with respect to a plane in space is achieved by taking advantage of the inherent symmetry of the spherical harmonics forming the encoding and decoding matrices. You compute the transformation matrix by sign-inverting channels associated with odd-symmetric spherical harmonics [1].

Up-Down Mirroring

Create Transformation Matrix

You achieve up-down mirroring by inverting the signs of odd-symmetric spherical harmonics with respect to the plane defined by z=0. This is equivalent to multiplying each harmonic by ${\left(-1\right)}^{\mathit{m}+\mathit{n}}$, where n is the degree of the harmonic, and m is the index of the harmonic (see section 5.2.1 in [1]).

Assume the ambisonic order is equal to 2. The transformed coefficients are computed as follows.

order = 2;
cUpDown = zeros(1,(order+1)^2);
count = 1;
for n=0:order
    for m=-n:n
        cUpDown(count) = (-1)^(n+m);
        count = count+1;
    end
end

The transformation matrix is the diagonal matrix formed by these coefficients.

TUpDown = diag(cUpDown);

Verify Transformation

To verify this transformation, encode a sound source at known azimuth and elevation angles (in degrees).

azi = 30;
ele = 45;
source = [azi ele];
E = ambisonicEncoderMatrix(order,source);

Decode the ambisonic signal into a 4th degree t-design loudspeaker setup [2].

Get the cartesian coordinates of the t-design.

loudspeakerXYZ = getTDesign();

Plot the loudspeakers in space.

figure
k1 = convhull(loudspeakerXYZ(:,1),loudspeakerXYZ(:,2),loudspeakerXYZ(:,3),Simplify=true);
trisurf(k1,loudspeakerXYZ(:,1),loudspeakerXYZ(:,2),loudspeakerXYZ(:,3),FaceColor="cyan")
axis equal
xlabel("x (m)")
ylabel("y (m)")
zlabel("z (m)")

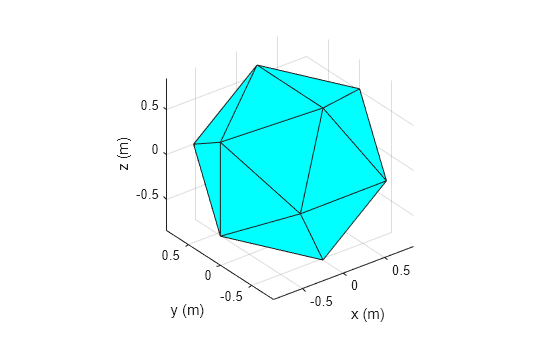
Convert the loudspeaker cartesian coordinates to spherical coordinates.

loudspeakerSph = zeros(size(loudspeakerXYZ,1),2);
[loudspeakerSph(:,1),loudspeakerSph(:,2)] = cart2sph(loudspeakerXYZ(:,1),loudspeakerXYZ(:,2),loudspeakerXYZ(:,3));
loudspeakerSph = 180*loudspeakerSph/pi;

Design the decoding matrix.

D = ambisonicDecoderMatrix(order,loudspeakerSph);

Decode the ambisonic signal while applying the up-down transformation.

Y = E*TUpDown*D;

Scale the loudspeaker direction vectors by the respective decoded gains and combine them to get the equivalent decoded sound direction.

rV = Y.^2*loudspeakerXYZ;
[azi1,ele1] = cart2sph(rV(1),rV(2),rV(3));
azi1 = 180*azi1/pi;
ele1 = 180*ele1/pi;

Display the azimuth and elevation values of the original and decoded signal. As expected, the azimuth value is unchanged, and the elevation's sign is flipped, which indicates mirroring with respect to the horizontal (z=0) plane.

fprintf("Original source: [%f, %f]\n",azi,ele)

Original source: [30.000000, 45.000000]

fprintf("Decoded source (up-down): [%f, %f]\n",azi1,ele1)

Decoded source (up-down): [30.000000, -45.000000]

Left-Right Mirroring

You achieve left-right mirroring by inverting the signs of harmonics where m<0 (see section 5.2.1 in [1]).

Compute the transformed coefficients.

cLeftRight = zeros(1,(order+1)^2);
count = 1;
for n=0:order
    for m=-n:n
        cLeftRight(count) = (-1)^(m<0);
        count = count+1;
    end
end

Compute the transformation matrix.

TLeftRight = diag(cLeftRight);

Decode the ambisonic signal while applying the left-right transformation.

Y = E*TLeftRight*D;

Compute the direction of the decoded sound.

rV = Y.^2*loudspeakerXYZ;
[azi1,ele1] = cart2sph(rV(1),rV(2),rV(3));
azi1 = 180*azi1/pi;
ele1 = 180*ele1/pi;

Display the azimuth and elevation values of the decoded signal. As expected, the elevation value is unchanged, and the azimuth value's sign is flipped, indicating mirroring with respect to the vertical (x=0) plane.

fprintf("Original source: [%f, %f]\n",azi,ele)

Original source: [30.000000, 45.000000]

fprintf("Decoded source (left-right): [%f, %f]\n",azi1,ele1)

Decoded source (left-right): [-30.000000, 45.000000]

Front-Back Mirroring

You achieve front-back mirroring by inverting the signs of every odd-numbered m>0 harmonic or even-numbered harmonic with m<0 (see section 5.2.1 in [1]).

Compute the transformed coefficients.

cFrontBack = zeros(1,(order+1)^2);
count = 1;
for n=0:order
    for m=-n:n
        cFrontBack(count) = (-1)^(m+(m<0));
        count = count+1;
    end
end

Compute the transformation matrix.

TFrontBack = diag(cFrontBack);

Decode the ambisonic signal while applying the left-right transformation.

Y = E*TFrontBack*D;

Compute the direction of the decoded sound.

rV = Y.^2*loudspeakerXYZ;
[azi1,ele1] = cart2sph(rV(1),rV(2),rV(3));
azi1 = 180*azi1/pi;
ele1 = 180*ele1/pi;

Display the azimuth and elevation values of the decoded signal. As expected, the elevation value is unchanged, and the azimuth value is mirrored with respect to the y=0 plane.

fprintf("Original source: [%f, %f]\n",azi,ele)

Original source: [30.000000, 45.000000]

fprintf("Decoded source (front-back): [%f, %f]\n",azi1,ele1)

Decoded source (front-back): [150.000000, 45.000000]

3-D Rotation

In this section, you perform a general rotation of an ambisonic signal around the x-axis (pitch), the y-axis (roll), and the z-axis (yaw).

Define the desired roll, pitch and yaw values (all in degrees).

roll0 = 50; 
pitch0 = 10;
yaw0 = 15;

Since you achieve the effect by rotating virtual loudspeakers instead of the actual source, invert the sign of the angles.

roll = -roll0; 
pitch = -pitch0;
yaw = -yaw0;

Compute the roll, pitch and yaw rotation matrices.

rollRad = roll*pi/180;
rollMAT = [1 0 0;0 cos(rollRad) -sin(rollRad);0 sin(rollRad) cos(rollRad)];

pitchRad = pitch*pi/180;
pitchMAT = [cos(pitchRad) 0 sin(pitchRad);0 1 0;-sin(pitchRad) 0 cos(pitchRad)];

yawRad = yaw*pi/180;
yawMAT = [cos(yawRad) -sin(yawRad) 0; sin(yawRad) cos(yawRad) 0;0 0 1];

Combine the individual matrices into the rotation matrix.

R = rollMAT*pitchMAT*yawMAT;

Apply the rotation matrix to a virtual loudspeaker setup.

rotatedSpkCart = (R * loudspeakerXYZ.').'; 

Convert the rotated loudspeaker coordinates to the spherical domain:

[rotatedSpkAzi, rotatedSpkEle] = cart2sph(rotatedSpkCart(:,1), ...
    rotatedSpkCart(:,2), rotatedSpkCart(:,3));

Re-encode the locations of the rotated loudspeakers.

E2 = ambisonicEncoderMatrix(order,180*[rotatedSpkAzi, rotatedSpkEle]/pi);

Create the transformation matrix (see equation (5.6) in [1]).

TRotation = (D*E2).';

Decode the ambisonic signal while applying the rotation.

Y = E*TRotation*D;

Determine the effective location of the decoded source.

rV = Y.^2*loudspeakerXYZ;
[azi1,ele1] = cart2sph(rV(1),rV(2),rV(3));
fprintf("Rotation: [%f, %f]\n",180*azi1/pi,180*ele1/pi)

Rotation: [-8.329645, 37.445025]

Compare the decoded source location with the expected location by rotating the original source location by the desired pitch, roll and yaw values:

transformMatrix = ...
    makehgtform('zrotate',pi*yaw0/180,'yrotate',pi*pitch0/180,'xrotate',pi*roll0/180);

[sourceXYZ(1),sourceXYZ(2),sourceXYZ(3)] = sph2cart(source(1)*pi/180,source(2)*pi/180,1); 
rotatedSrcCart  = (transformMatrix(1:3,1:3) * sourceXYZ.');  

[newSourceAzi,newSourceele] = cart2sph(rotatedSrcCart(1),rotatedSrcCart(2),rotatedSrcCart(3));
fprintf("Expected Rotation: [%f, %f]\n",180*newSourceAzi/pi,180*newSourceele/pi)

Expected Rotation: [-8.329645, 37.445025]

Apply Transformation to Speech Signal

To better illustrate the effect, apply the effect to an ambisonic-encoded speech signal.

Read the mono audio signal.

filename = "CleanSpeech-48-mono-3secs.ogg";
[audioIn,fs] = audioread(filename);

Encode the signal with the desired location.

location = [90 0];
z = audioIn*ambisonicEncoderMatrix(order,location);

Decode the signal and apply left-right mirroring.

effect = "left-right mirroring";
y = z*D;

switch effect
    case "left-right mirroring"
        T = TLeftRight;
    case "up-down mirroring"
        T = TUpDown;
    case "front-back mirroring"
        T = TFrontBack;
    case "3D rotation"
        T = TRotation;
end
yTranform = z*T*D;

Convert the decoded signal into binaural audio.

First, load an HRTF dataset.

ARIDataset = sofaread("ReferenceHRTF.sofa");

Compute the corresponding impulse responses by interpolating the HRTF dataset.

filters = interpolateHRTF(ARIDataset,loudspeakerSph,Algorithm="vbap");

Create an FIR filter to perform binaural HRTF filtering based on the position of the virtual loudspeakers.

filters = permute(filters,[2 1 3]);
filters = reshape(filters,size(filters,1)*size(filters,2),[]);
filt = dsp.MIMOFIRFilter(filters, SumFilteredOutputs=true);

Create and plot the effect-free stereo signal.

audioOut = filt(y);
audioOut = audioOut/max(abs(audioOut(:)));
release(filt)

figure
t = (0:length(audioOut)-1)/fs;
subplot(211)
plot(t, audioOut(:,1))
grid on
title("Right Ear")
subplot(212)
plot(t, audioOut(:,2))
grid on
xlabel("time (s)")
title("Left Ear")

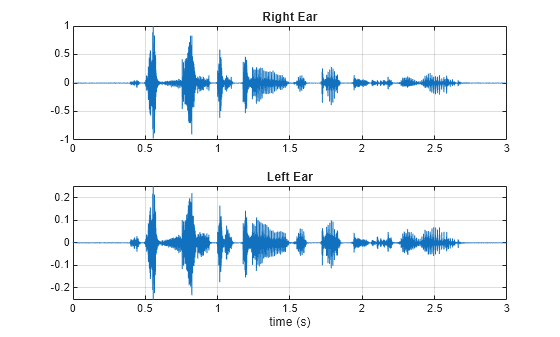
Create and plot the output stereo signal when the effect is applied.

audioOutTranform = filt(yTranform);
audioOutTranform = audioOutTranform/max(abs(audioOutTranform(:)));

figure
subplot(211)
plot(t, audioOutTranform(:,1))
grid on
title("Right Ear")
subplot(212)
plot(t, audioOutTranform(:,2))
grid on
xlabel("time (s)")
title("Left Ear")

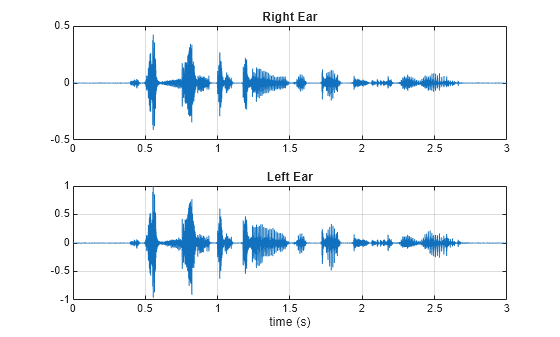
Listen to the effect-free decoded stereo signal.

ainfo = audioinfo(filename);
sound(audioOut,fs)
pause(ainfo.Duration)

Listen to the mirrored decoded stereo signal.

sound(audioOutTranform,fs)
pause(ainfo.Duration)

Rotate Ambisonic Signal with an Audio Plugin

audiopluginexample.AmbisonicBinauralizer is an audio plugin that performs binauralization of an ambisonic-encoded signal following the steps highlighted in the previous section. The plugin also allows you to rotate the sound field by applying desired roll, pitch and yaw.

In this section, you use the audio plugin to rotate an ambisonic signal in real-time.

Set up an audio file reader to read an ambisonic-encoded signal frame-by-frame.

samplesPerFrame = 2048;
fileReader = dsp.AudioFileReader("Heli_16ch_ACN_SN3D.wav", ...
                    SamplesPerFrame=samplesPerFrame);

Set up an audio device writer to listen to the output rotated binaural signal. Set the writer's sample rate to the audio file's sample rate.

deviceWriter = audioDeviceWriter;
myInfo = audioinfo("Heli_16ch_ACN_SN3D.wav");
deviceWriter.SampleRate = myInfo.SampleRate;

Instantiate the audio plugin.

decoder = audiopluginexample.AmbisonicBinauralizer;

Set the decoder's sample rate to the ambisonic file's sample rate.

setSampleRate(decoder,myInfo.SampleRate)

Launch the decoder's parameter tuner.

parameterTuner(decoder)

In a streaming loop, decode and binauralize the ambisonic signal. Rotate the signal by modifying values of roll, pitch and yaw using the parameter tuner. Listen to the binaural output signal.

while ~isDone(fileReader)
    audioAmbi = fileReader();
    audioDecoded = process(decoder,audioAmbi);
    numUnderrun = deviceWriter(audioDecoded); 
end

% Release resources
release(fileReader)
release(deviceWriter)

Helper Functions

function xyz = getTDesign()
% Order-4 t-design loudspeaker setup

% "McLaren's Improved Snub Cube and Other New Spherical Designs in
% Three Dimensions", R. H. Hardin and N. J. A. Sloane, Discrete and
% Computational Geometry, 15 (1996), pp. 429-441.

xyz = [0.850650808352000               0  -0.525731112119000
   0.525731112119000  -0.850650808352000                   0
                   0  -0.525731112119000   0.850650808352000
   0.850650808352000                   0   0.525731112119000
  -0.525731112119000  -0.850650808352000                   0
                   0   0.525731112119000  -0.850650808352000
  -0.850650808352000                   0  -0.525731112119000
  -0.525731112119000   0.850650808352000                   0
                   0   0.525731112119000   0.850650808352000
  -0.850650808352000                   0   0.525731112119000
   0.525731112119000   0.850650808352000                   0
                   0  -0.525731112119000  -0.850650808352000];
end

References

[1] "Ambisonics, A Practical 3D Audio Theory for Recording, Studio Production, Sound Reinforcement, and Virtual Reality," Zotter and Frank, Springer Topics in Signal Processing, Volume 19, 2019.

[2] "McLaren's Improved Snub Cube and Other New Spherical Designs in Three Dimensions", R. H. Hardin and N. J. A. Sloane, Discrete and Computational Geometry, 15 (1996), pp. 429-441.