Digital Up-Converter

Interpolate and translate digital signal from baseband to intermediate frequency (IF) band

• 

Libraries:
DSP System Toolbox / Signal Operations

Description

The Digital Up-Converter (DUC) block converts a complex digital baseband signal to a real passband signal.

The DUC block upsamples the input signal using a cascade of three interpolation filters. The block frequency upconverts the upsampled signal by multiplying it by the specified center frequency of the output signal. This block designs the interpolation filters according to the filter parameters you set in the block dialog box.

Examples

Digital Up and Down Conversion for Family Radio Service in Simulink

Implement Family Radio Service system using Digital Down-Converter and Digital Up-Converter blocks.

• Open Script

Ports

Input

Input 1 — Input signal

column vector

Specify the input signal as a column vector of real or complex values.

When the input data type is double or single precision, the output data type is the same as that of the input. When the input data type is a signed integer or fixed-point, the output data type is defined by the Output parameter on the Data Types tab.

Data Types: single | double | int8 | int16 | int32 | int64 | fixed point
Complex Number Support: Yes

Output

Output 1 — Upconverted and upsampled signal

column vector

The block outputs the upconverted and upsampled signal as a column vector of real values. The length of the output is equal to the length of the input multiplied by the value that you specify in the Interpolation factor parameter.

When the input data type is double or single precision, the output data type is the same as that of the input. When the input data type is a signed integer or fixed-point, the output data type is defined by the Output parameter on the Data Types tab.

Data Types: single | double | int8 | int16 | int32 | int64 | fixed point

Parameters

Main Tab

Interpolation factor — Interpolation factor

100 (default) | positive integer > 1 | vector of positive integers

Specify the interpolation factor as a positive integer > 1, or as a 1-by-2 or 1-by-3 vector of positive integers.

When you set this parameter to a scalar value, the block applies the same interpolation factor to the three interpolation filtering stages.

When you set this parameter to a 1-by-2 vector, the block applies the second and third values in the vector to the second and third filtering stages, respectively, and bypasses the first filter stage. Both elements of the Interpolation factor must be greater than 1.

When you set this parameter to a 1-by-3 vector, the block applies the values in the vector to the corresponding filtering stages. The second and third elements of Interpolation factor must be greater than 1, and the first element must be 1 or 2.

Minimum order filter design — Design minimum-order filter

on (default) | off

When you select this check box, the block designs filters with the minimum possible order that meets the requirements specified in these parameters:

• Passband ripple of cascade response (dB)

• Stopband attenuation of cascade response (dB)

• Two sided bandwidth of input signal

• Source of stopband frequency

• Stopband frequency

When you clear this check box, the block designs filters with orders that you specify in Order of first filter stage, Order of CIC compensation filter stage, and Number of sections of CIC interpolator. The filter designs meet the passband and stopband frequency specifications that you set in Two sided bandwidth of input signal, Source of stopband frequency, and Stopband frequency. By default, this check box is selected.

Order of first filter stage — Order of first filter stage

10 (default) | positive even integer

Specify the order of the first filter stage as an even positive integer. When you specify Interpolation factor as a 1-by-2 vector, the block ignores the value in this parameter because the block bypasses the first filter stage.

Dependencies

To enable this parameter, clear the Minimum order filter design parameter.

Number of sections of CIC interpolator — Number of sections of CIC interpolator

3 (default) | positive integer

Specify the number of sections in the CIC interpolator as a positive integer.

Dependencies

This parameter appears when you clear the Minimum order filter design parameter.

Source of stopband frequency — Source of stopband frequency

Auto (default) | Property

Specify the source of the stopband frequency as Auto or Property.

When you set this parameter to Auto and set:

• Sample rate mode to Specify on dialog or Inherit from input port –– The block places the cutoff frequency of the cascade filter response at approximately F_c = SampleRate/2 Hz, and computes the stopband frequency as F_stop = F_c + TW/2. SampleRate is computed as 1/Ts, where Ts is the sample time of the input signal. TW is the transition bandwidth of the cascade response, computed as 2×(F_c–F_p), and the passband frequency F_p equals Bandwidth/2.

• Sample rate mode to Use normalized frequency (0 to 1) –– The block places the cutoff frequency of the cascade filter response at approximately F_c = 1/L, where L is the total interpolation factor specified in Interpolation factor, and computes the stopband frequency as F_stop = F_c + TW/2. TW is the transition bandwidth of the cascade response, computed as 2×(F_c–F_p), and the passband frequency F_p equals Bandwidth/2.

When you set this parameter to Property, specify the stopband frequency in the Stopband frequency parameter.

Type of oscillator — Type of oscillator

Sine wave (default) | NCO

Specify the oscillator type as one of the following:

• Sine wave (default) — The block performs frequency upconversion on the output of the interpolation filter cascade using a complex exponential signal obtained from samples of a sinusoidal trigonometric function.

• NCO — The block performs frequency upconversion with a complex exponential obtained using a numerically controlled oscillator (NCO).

Center frequency of output signal — Center frequency of output signal

0.9333 (default) | positive scalar

Specify the center frequency of the output signal as a positive scalar in Hz or in normalized frequency units (since R2024b).

If you set the Sample rate mode parameter to:

• Specify on dialog or Inherit from input port –– The value of the center frequency is in Hz and must be less than or equal to half the product of the SampleRate times the total interpolation factor. SampleRate is computed as 1/ Ts, where Ts is the sample time of the input signal. The block upconverts the input signal so that the output spectrum centers at the frequency you specify in Center frequency of output signal.

• Use normalized frequency (0 to 1) –– The value of the center frequency is in normalized frequency units. The value must be a positive scalar less than or equal to 1.0.

(since R2024b)

Order of CIC compensation filter stage — Order of CIC compensation filter stage

12 (default) | positive integer

Specify the order of the CIC compensation filter stage as a positive integer.

Dependencies

To enable this parameter, clear the Minimum order filter design parameter.

Two sided bandwidth of input signal — Two-sided bandwidth of input signal

0.0133 (default) | positive scalar

Specify the two-sided bandwidth of the input signal as a positive scalar in Hz or in normalized frequency units (since R2024b). The block sets the passband frequency of the cascade of filters to half of the value you specify in this parameter.

Stopband frequency — Stopband frequency

0.01 (default) | positive scalar

Specify the stopband frequency as a positive scalar in Hz or in normalized frequency units (since R2024b).

Dependencies

To enable this parameter, set the Source of stopband frequency to Property.

Passband ripple of cascade response (dB) — Passband ripple of cascade response

0.1 (default) | positive scalar

Specify the passband ripple of the cascade response in dB as a double-precision positive scalar. When you select the Minimum order filter design parameter, the block designs the filters so that the cascade response meets the passband ripple that you specify in Passband ripple of cascade response (dB).

Dependencies

To enable this parameter, select the Minimum order filter design parameter.

Stopband attenuation of cascade response (dB) — Stopband attenuation of cascade response

60 (default) | positive scalar

Specify the stopband attenuation of the cascade response in dB as a double-precision positive scalar. When you select the Minimum order filter design parameter, the block designs the filters such that the cascade response meets the stopband attenuation that you specify in this parameter.

Dependencies

To enable this parameter, select the Minimum order filter design parameter.

Number of NCO accumulator bits — Number of NCO accumulator bits

16 (default) | positive integer

Specify the number of NCO accumulator bits as an integer scalar in the range [1 128].

Dependencies

To enable this parameter, set Type of oscillator to NCO.

Number of NCO quantized accumulator bits — Number of NCO quantized accumulator bits

12 (default) | positive integer

Specify the number of NCO quantized accumulator bits as an integer scalar in the range [1 128]. This value must be less than the value you specify in Number of NCO accumulator bits.

Dependencies

To enable this parameter, set Type of oscillator to NCO.

Dither control for NCO — Dither control for NCO

on (default) | off

When you select this parameter, the block applies dither to the NCO signal according to the number of dither bits you specify in Number of NCO dither bits.

Dependencies

To enable this parameter, set Type of oscillator to NCO.

Number of NCO dither bits — Number of NCO dither bits

4 (default) | positive integer

Specify the number of NCO dither bits as an integer scalar smaller than the number of accumulator bits in Number of NCO accumulator bits.

Dependencies

To enable this parameter, set Type of oscillator to NCO and select the Dither control for NCO parameter.

Sample rate mode — Mode to specify input sample rate

Use normalized frequency (0 to 1) (default) | Specify on dialog | Inherit from input port

Since R2024b

Specify the input sample rate using one of these options:

• Use normalized frequency (0 to 1) –– Specify the center frequency, two-sided bandwidth, and stopband frequency in normalized frequency units (0 to 1).

• Specify on dialog –– Specify the input sample rate in the block dialog box using the Input sample rate (Hz) parameter.

• Inherit from input port –– The block inherits the sample rate from the input signal. The block computes the sample rate as N/Ts, where N is the frame size of the input signal, and Ts is the sample time of the input signal.

Input sample rate (Hz) — Sample rate of input signal

300e3 (default) | positive scalar

Specify the sample rate of the input signal in Hz as a positive scalar. The value of this parameter multiplied by the total interpolation factor must be greater than or equal to twice the value in Center frequency of output signal.

Dependencies

To enable this parameter, set the Sample rate mode parameter to Specify on dialog. (since R2024b)

View Filter Response — View Filter Response

button

Click this button to open the Filter Visualization Tool (FVTool) and display the magnitude and phase response of each stage as well as the cascade of stages in the Digital Up-Converter. The response is based on the values you specify in the block parameters dialog box. Changes made to these parameters update FVTool.

To update the magnitude response while FVTool is running, modify the parameters in the dialog box and click Apply.

Simulate using — Type of simulation to run

Interpreted execution (default) | Code generation

Specify the type of simulation to run. You can set this parameter to:

• Interpreted execution –– Simulate model using the MATLAB^® interpreter. This option shortens startup time.

• Code generation –– Simulate model using generated C code. The first time you run a simulation, Simulink^® generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.

Data Types Tab

Stage output — Stage output

Inherit: Same as input (default) | fixdt([],16,0)

Specify the data type of the output in the first, second, and third filter stages. You can set this parameter to:

• Inherit: Same as input (default) — The block inherits the Stage output data type from the input signal.

• fixdt([],16,0) — The block uses the fixed-point data type with binary-point scaling. Specify the sign mode of this data type as [] or true.

• An expression that evaluates to a data type, for example, numerictype([],16,15). Specify the sign mode of this data type as [] or true.

The block casts the data at the output of each filter stage according to the value you set in this parameter. For the CIC stage, the casting is done after the signal has been scaled by the normalization factor.

For help with setting the stage output parameter, you can click the Show data type assistant button to display the data type assistant.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

Output — Output

Inherit: Same as input (default) | fixdt([],16,0)

Specify the data type of the block output. You can set this parameter to:

• Inherit: Same as input (default) — The block Inherits the output datatype from the input.

• fixdt([],16,0) — The block uses the fixed-point data type with binary-point scaling. Specify the sign mode of this data type as [] or true.

• An expression that evaluates to a data type, for example, numerictype([],16,15). Specify the sign mode of this data type as [] or true.

For help with setting the Output parameter, you can click the Show data type assistant button to display the data type assistant..

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

Minimum — Minimum

[] (default) | scalar

Specify the minimum value of the block output. The default value is [] (unspecified). Simulink software uses this value to perform:

• Simulation range checking (see Specify Signal Ranges (Simulink))

• Automatic scaling of fixed-point data types

Maximum — Maximum

[] (default) | scalar

Specify the maximum value of the block output. The default value is [] (unspecified). Simulink software uses this value to perform:

• Simulation range checking (see Specify Signal Ranges (Simulink))

• Automatic scaling of fixed-point data types

Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types

off (default) | on

Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.

Block Characteristics

Data Types	double | fixed point | integer | single
Direct Feedthrough	no
Multidimensional Signals	no
Variable-Size Signals	no
Zero-Crossing Detection	no

More About

Fixed Point

The block diagram represents the DUC arithmetic with signed fixed-point inputs.

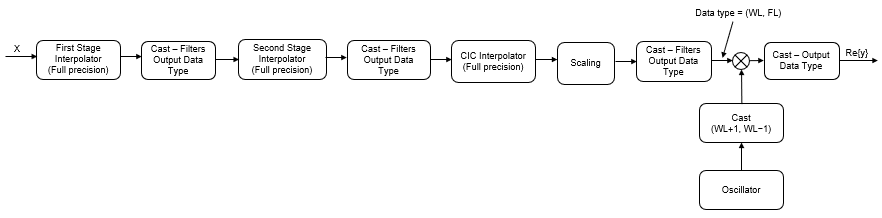
• WL is the word length of the input, and FL is the fraction length of the input.

• The output of each filter is cast to the filter output data type. In the dsp.DigitalUpConverter object, you can specify the filter output data type through the FiltersOutputDataType and CustomFiltersOutputDataType properties. In the Digital Up-Converter block, you can specify the filter output data type through the Stage output parameter. The casting of the CIC output occurs after the scaling factor is applied.

• The oscillator output is cast to a word length equal to the filter output data type word length plus one. The fraction length is equal to the filter output data type word length minus one.

• The scaling at the output of the CIC interpolator consists of coarse-gain and fine-gain adjustments. The coarse gain is achieved using the reinterpretcast (Fixed-Point Designer) function on the CIC interpolator output. The fine gain is achieved using full-precision multiplication.

The figure shows the coarse-gain and fine-gain operations.

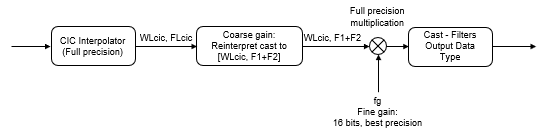
If the normalization gain is G (where 0<G≦1), then:

• WL_cic is the word length of the CIC interpolator output, and FL_cic is the fraction length of the CIC interpolator output.

• F1 = abs(nextpow2(G)), indicating the part of G achieved by using bit shifts (coarse gain).

• F2 is the fraction length specified by the filter output data type.

• fg = fi((2^F1)*G,true,16), which indicates that the remaining gain cannot be achieved with a bit shift (fine gain).

HDL Code Generation

For a hardware-optimized digital upconverter algorithm that supports HDL code generation, see Implement Digital Upconverter for FPGA (DSP HDL Toolbox). This example uses DSP HDL Toolbox™ blocks that have hardware-friendly valid and reset control signals, and models exact hardware latency behavior. The Simulink model in the example supports HDL code generation with HDL Coder™ tools.

You can model the same algorithm in MATLAB by using DSP HDL Toolbox System objects.

Algorithms

The digital up converter upsamples the input signal using a cascade of three interpolation filters. This algorithm frequency-upconverts the upsampled signal by multiplying it with a complex exponential that has the specified center frequency. In this case, the filter cascade consists of an FIR interpolation stage, a second stage for CIC compensation, and a CIC interpolator. The block diagram shows the architecture of the digital up converter.

The scaling section normalizes the CIC gain and the oscillator power. It can also contain a correction factor to achieve the desired ripple specification. Depending on how you set the interpolation factor, the block bypasses the first filter stage. When the input data type is floating point, the algorithm implements an N-section CIC interpolation filter as a FIR filter with a response that corresponds to a cascade of N boxcar filters. The algorithm emulates a CIC filter with an FIR filter so that you can run simulations with floating-point data. When the input data type is a fixed-point type, the algorithm implements a true CIC filter with actual comb and integrator sections.

This block diagram represents the DUC arithmetic with floating-point inputs.

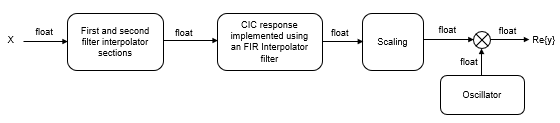
For details about fixed-point operation, see Fixed Point.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2015a

R2024b: Support for normalized frequencies

When you set the Sample rate mode parameter to Use normalized frequency (0 to 1), you can specify the two-sided bandwidth of the input signal, center frequency of the output signal, and the stopband frequency in normalized frequency units (0 to 1).

R2024a: Change in the default value of Simulate using parameter

The default value of the Simulate using parameter is now Interpreted execution. With this change, the block uses the MATLAB interpreter for simulation by default.