Normalization
Perform vector normalization along rows, columns, or specified dimension
Libraries:
DSP System Toolbox /
Math Functions /
Math Operations
Description
The Normalization block independently normalizes each row, column, or
vector of the specified dimension of the input using the Squared
2-norm or the 2-norm methods.
For more information on how the block normalizes the signal, see Algorithms.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
Algorithms
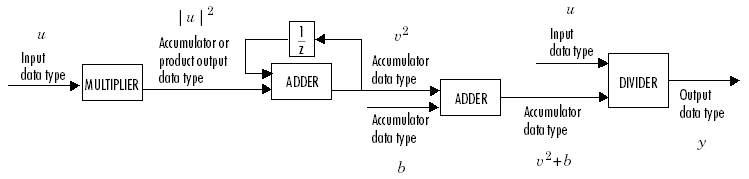
This block treats an arbitrarily dimensioned input U as a collection of vectors oriented along the specified dimension. The block normalizes these vectors by either their norm or the square of their norm.
For example, consider a 3-D input U(i,j,k) and assume that you want to normalize along the second dimension. First, define the 2-D intermediate quantity V(i,k) such that each element of V is the norm of one of the vectors in U
Given V, the output of the block Y(i,j,k) in 2-norm mode is given by
In squared 2-norm mode, the block output is given by
The normalization bias b is typically chosen to be a small positive constant (for example, 1e-10) that prevents potential division by zero.
Extended Capabilities
Version History
Introduced before R2006a