Recognize Handwritten Digits Zero to Nine Using MNIST Data Set on STM32 Processor Boards
This example shows how to use Embedded Coder® Support Package for STMicroelectronics® STM32 Processors to recognize digits from zero to nine. The algorithm used in this example recognizes the digits and then outputs a label for the digit.
This example uses a pretrained network, mnistData.mat, for prediction. The network has been trained using the Modified National Institute of Standards and Technology database (MNIST) data set.
The MNIST data set is a commonly used data set in the field of neural networks. This data set comprises of 60,000 training and 10,000 testing grayscale images for machine learning models. Each image is 28-by-28 pixels.
Prerequisites
Complete the Getting Started with STMicroelectronics STM32 Processor Based Boards tutorial.
Required MathWorks Products
In addition to the products listed under 'This example uses:', the following product is also required.
MATLAB Coder Interface for Deep Learning. To install this support package, select it from the MATLAB Add-Ons menu.
Required Hardware
To run this example you need the following hardware:
Board based on the STMicroelectronics STM32 Processor
Micro USB cable
Supported Boards
STM32 Nucleo H743ZI2
STM32 Nucleo L496ZG
STM32Nucleo F767ZI
STM32 F746G
STM32 Nucleo U575ZI-Q
STM32 L552ZE-Q
STM32 WB55RG
Configure Simulink Model and Calibrate Parameters
In this example, you classify images using deep learning on the MNIST dataset.
Open the RecognizeDigitsMnist Simulink model.
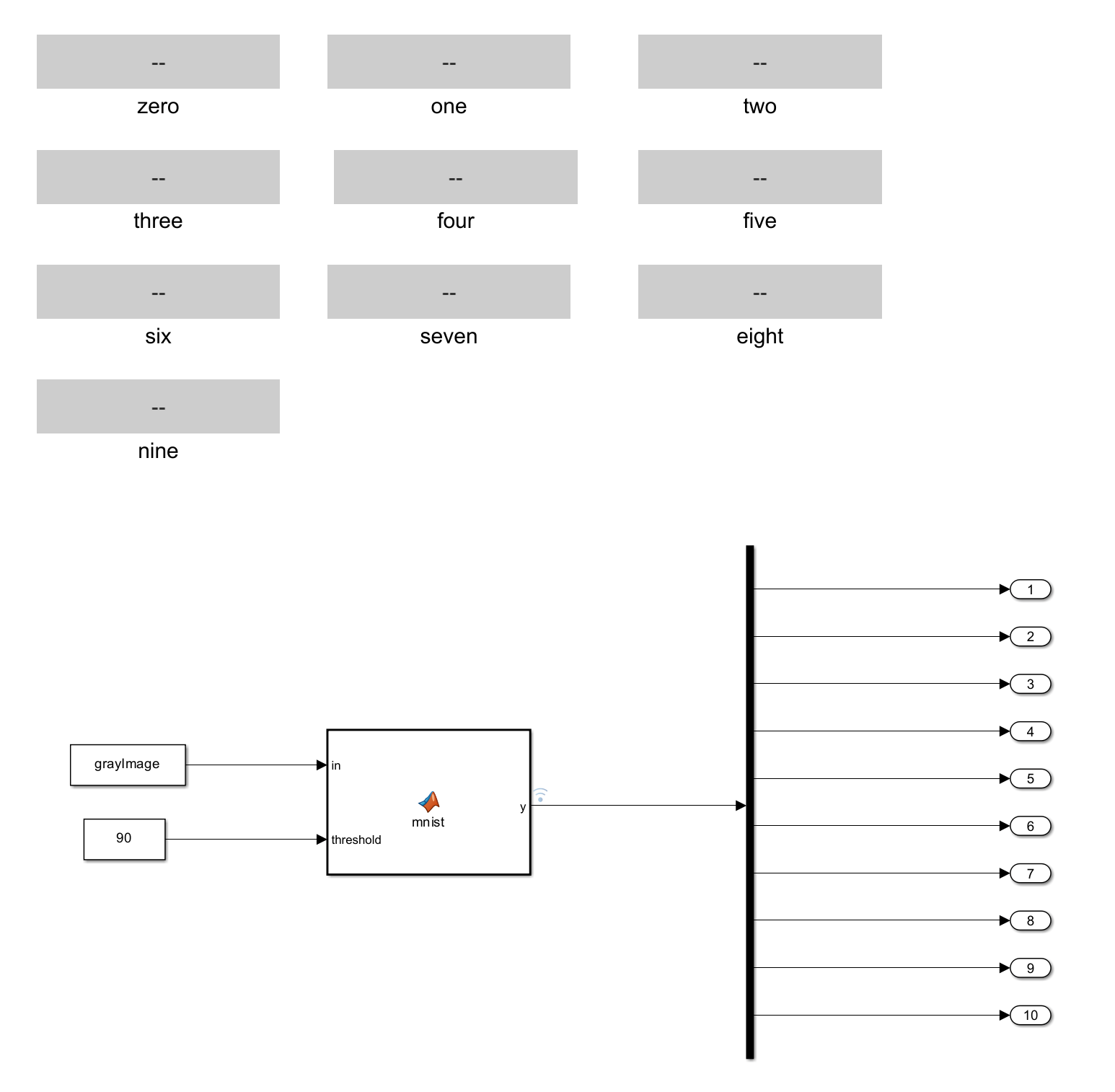
This model includes a MATLAB Function block with two Constant block inputs and a Demux output.
Image Input: The first input to the block is the grayscale image data, which is read from an image file using MATLAB's imread function. If the image is in the RGB format, you must resize and covert it to grayscale before inputing it to the MATLAB Function block. The final grayscale image must be 28-by-28 pixels in size.
Threshold Input: The second input to the MATLAB Function block is a threshold value. The block uses this value to determine the prediction criteria. The threshold value is typically a scalar that defines a specific limit or boundary for the processing algorithm.
Demux Output: This model uses demux to extract the components of the input vector signal from the MATLAB Function block and split them into separate signals.
The example uses a Simulink model RecognizeDigitsMnist.slx to generate the training data required to train the neural network. Run the following code to obtain the training data.
% Extract images digitDatasetPath = fullfile(matlabroot,'toolbox','nnet', ... 'nndemos','nndatasets','DigitDataset'); imds = imageDatastore(digitDatasetPath, ... 'IncludeSubfolders',true, ... 'LabelSource','foldernames'); % divide datastores numTrainingFiles = 750; [imdsTrain,imdsTest] = splitEachLabel(imds,numTrainingFiles,'randomize'); %Define the convolutional neural network architecture. layers = [ ... imageInputLayer([28 28 1]) convolution2dLayer(5,20) reluLayer maxPooling2dLayer(2,'Stride',2) fullyConnectedLayer(10) softmaxLayer classificationLayer]; %training options options = trainingOptions('sgdm', ... 'MaxEpochs',20,... 'InitialLearnRate',1e-4, ... 'Verbose',false, ... 'Plots','training-progress'); %train the network net = trainNetwork(imdsTrain,layers,options);
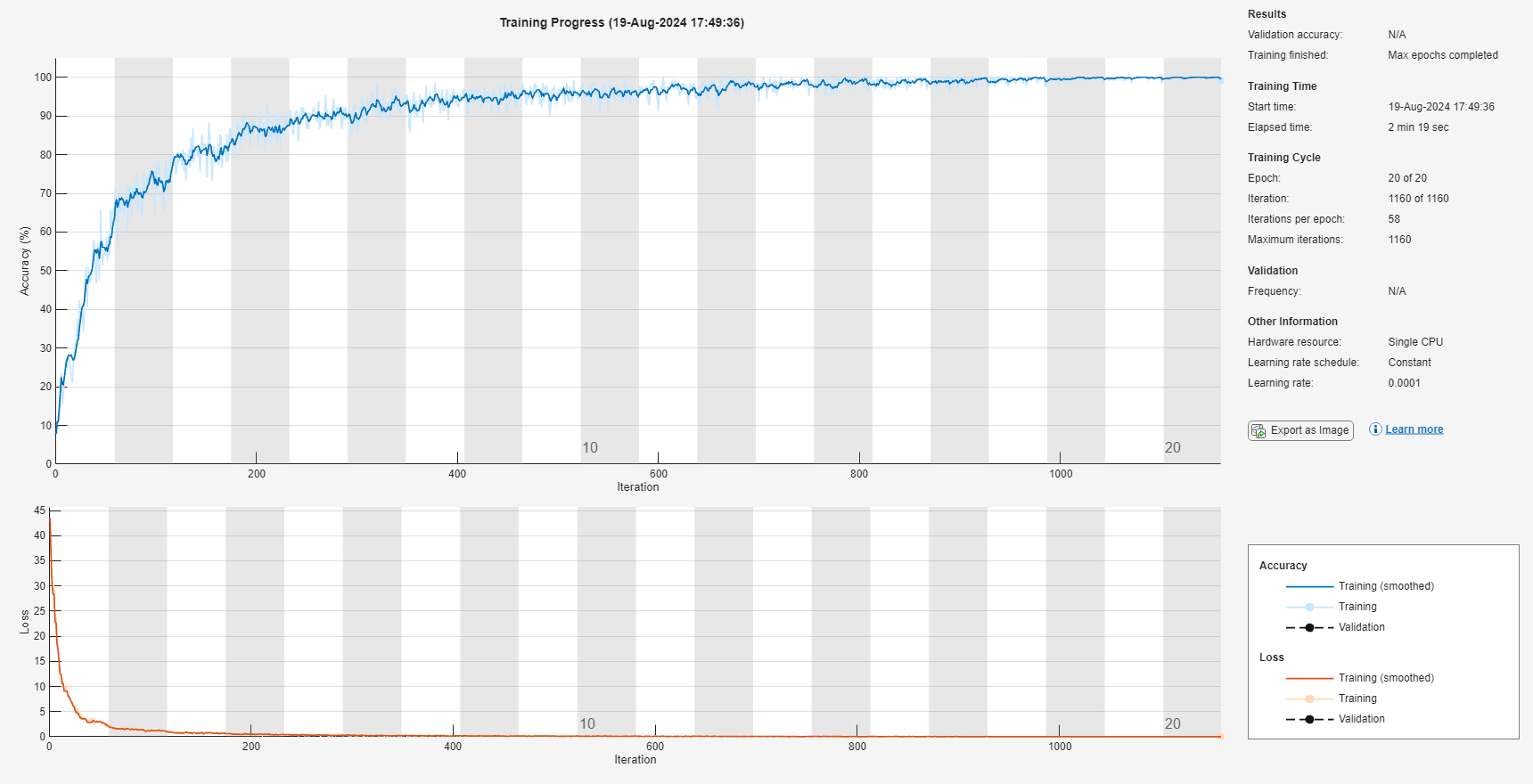
% accuracy of network YPred = classify(net,imdsTest); YTest = imdsTest.Labels; accuracy = sum(YPred == YTest)/numel(YTest); % saving the mnist data save("mnistData.mat", "net")
This code demonstrates how to train a neural network for digit classification using the data set. First, it loads images from the data set. It then splits the data set into training and validation sets, with 750 images per label allocated to training. The architecture includes an input layer for 28-by-28 grayscale images.
Run Simulink Model
In this example, the input image is the image of the digit 4 and the trained network recognizes the digit 4.
1. Input the image data using the Constant block. Perform these steps to input the image data.
Steps to Prepare Grayscale Image Data:
a. Read the Image File: Use the imread function to read the image file.
b. Resize the Image: Use the imresize function to resize the image to 28-by-28 pixels.
c. Convert to Grayscale: Use the rgb2gray function to convert the image to grayscale if it is in the RGB format.
d. Input into Constant Block: Store the final grayscale image data in a variable and set this variable as the value of the Constant block in Simulink.
Use this code to prepare the grayscale image data.
% Read the image file imageData = imread('image4.png'); % Check if the image is in RGB format if size(imageData, 3) == 3 % Resize the image to 28x28 pixels resizedImage = imresize(imageData, [28, 28]); % Convert the resized image to grayscale grayImage = rgb2gray(resizedImage); else % If the image is already grayscale, just resize it grayImage = imresize(imageData, [28, 28]); end
2. Input the threshold value.
3. On the Hardware tab of the Simulink model, click Monitor & Tune to run the Simulink model on the STM32 processor board.

4. Observe the Display blocks. The Display block four displays the output as 1, indicating an accurate recognition of the digit 4.
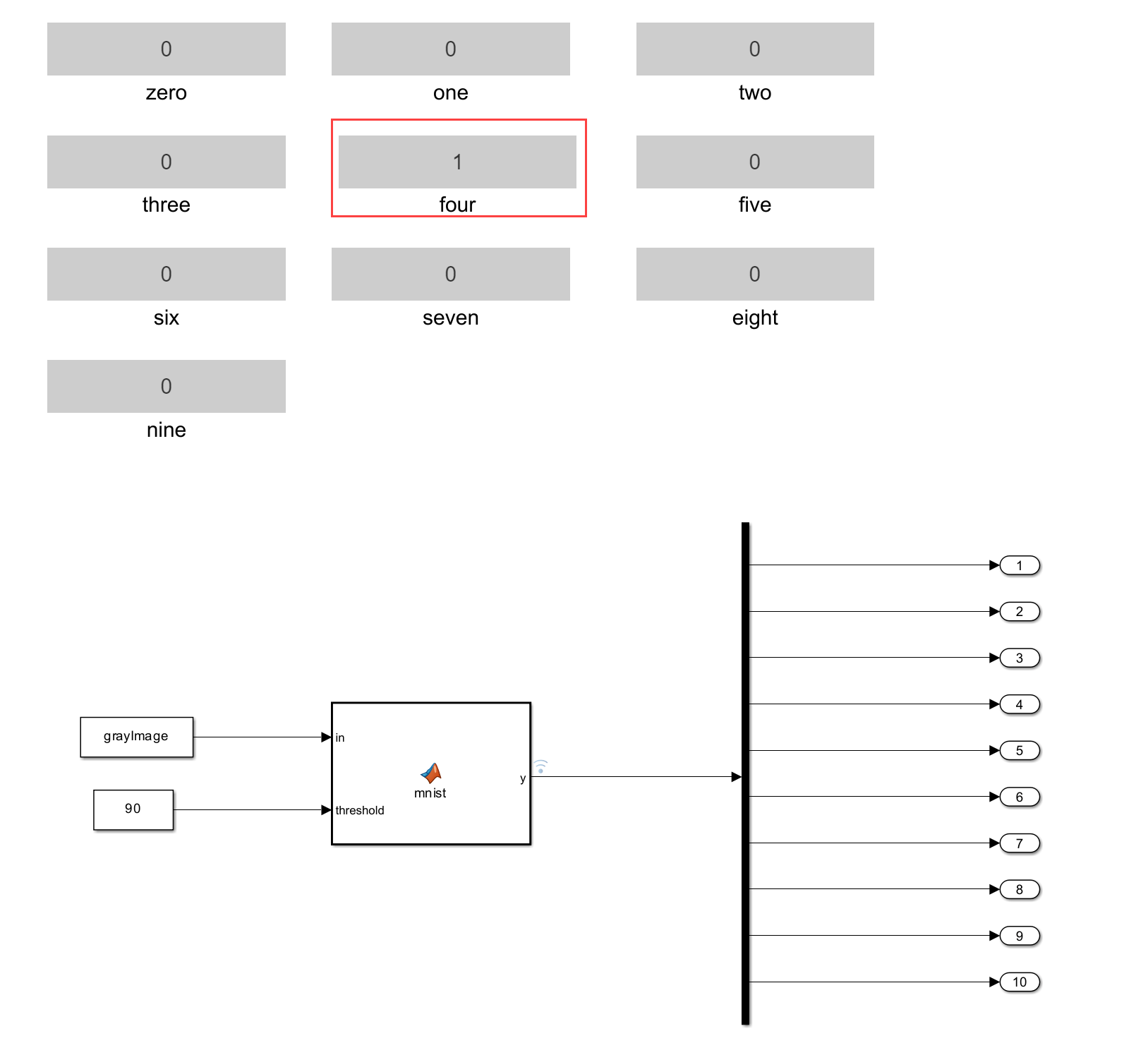
5. Click Stop to stop the Simulink model simulation.
Related Examples
See Also
List of Deep Learning Layers (Deep Learning Toolbox)
Deep Learning in MATLAB (Deep Learning Toolbox)
trainingOptions(Deep Learning Toolbox)