Questa pagina è stata tradotta con la traduzione automatica. Fai clic qui per vedere l'ultima versione in inglese.

Trova i minimi globali o multipli locali

Questo esempio illustra come GlobalSearch trova in modo efficiente un minimo globale e come MultiStart trova molti più minimi locali.

La funzione obiettivo per questo esempio ha molti minimi locali e un unico minimo globale. In coordinate polari, la funzione è

$f (r, t) = g (r) h (t)$

Dove

$\begin{array}{l} g (r) = (\sin (r) - \frac{\sin (2 r)}{2} + \frac{\sin (3 r)}{3} - \frac{\sin (4 r)}{4} + 4) \frac{r^{2}}{r + 1} \\ h (t) = 2 + \cos (t) + \frac{\cos (2 t - \frac{1}{2})}{2} . \end{array}$

Rappresenta graficamente le funzioni $g$ e $h$ e crea un grafico di superficie della funzione $f$ .

figure
subplot(1,2,1);
fplot(@(r)(sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) .* r.^2./(r+1), [0 20])
title(''); ylabel('g'); xlabel('r');
subplot(1,2,2);
fplot(@(t)2 + cos(t) + cos(2*t-1/2)/2, [0 2*pi])
title(''); ylabel('h'); xlabel('t');

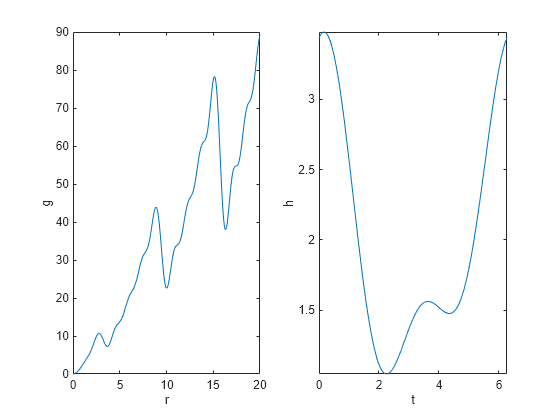
figure
fsurf(@(x,y) sawtoothxy(x,y), [-20 20])
% sawtoothxy is defined in the first step below
xlabel('x'); ylabel('y'); title('sawtoothxy(x,y)');
view(-18,52)

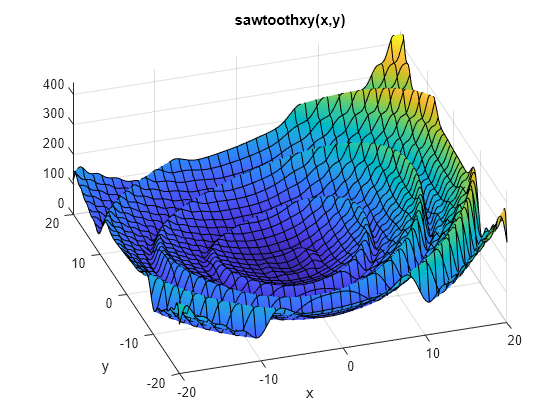
Il minimo globale è in $r = 0$ , con funzione obiettivo 0. La funzione $g (r)$ cresce approssimativamente linearmente in $r$ , con una forma a dente di sega ripetuta. La funzione $h (t)$ ha due minimi locali, uno dei quali è globale.

Il file sawtoothxy.m converte le coordinate cartesiane in quelle polari, quindi calcola il valore in coordinate polari.

type sawtoothxy

function f = sawtoothxy(x,y)
[t r] = cart2pol(x,y); % change to polar coordinates
h = cos(2*t - 1/2)/2 + cos(t) + 2;
g = (sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) ...
    .*r.^2./(r+1);
f = g.*h;
end

Singolo minimo globale tramite `GlobalSearch`

Per cercare il minimo globale utilizzando GlobalSearch, per prima cosa bisogna creare una struttura del problema. Utilizzare l'algoritmo 'sqp' per fmincon,

problem = createOptimProblem('fmincon',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fmincon,'Algorithm','sqp','Display','off'));

Il punto di partenza è [100,-50] anziché [0,0], quindi GlobalSearch non inizia dalla soluzione globale.

Convalidare la struttura del problema eseguendo fmincon .

[x,fval] = fmincon(problem)

x = 1×2

   45.7236 -107.6515

fval = 555.5820

Crea l'oggetto GlobalSearch e imposta la visualizzazione iterativa.

gs = GlobalSearch('Display','iter');

Per garantire la riproducibilità, impostare il valore seed del generatore di numeri casuali.

rng(14,'twister')

Esegui il risolutore.

[x,fval] = run(gs,problem)

 Num Pts                 Best       Current    Threshold        Local        Local                 
Analyzed  F-count        f(x)       Penalty      Penalty         f(x)     exitflag        Procedure
       0      200       555.6                                   555.6            0    Initial Point
     200     1463   1.547e-15                               1.547e-15            1    Stage 1 Local
     300     1564   1.547e-15     5.858e+04        1.074                              Stage 2 Search
     400     1664   1.547e-15      1.84e+05         4.16                              Stage 2 Search
     500     1764   1.547e-15     2.683e+04        11.84                              Stage 2 Search
     600     1864   1.547e-15     1.122e+04        30.95                              Stage 2 Search
     700     1964   1.547e-15     1.353e+04        65.25                              Stage 2 Search
     800     2064   1.547e-15     6.249e+04        163.8                              Stage 2 Search
     900     2164   1.547e-15     4.119e+04        409.2                              Stage 2 Search
     950     2359   1.547e-15           477        589.7          387            2    Stage 2 Local
     952     2423   1.547e-15         368.4          477        250.7            2    Stage 2 Local
    1000     2471   1.547e-15     4.031e+04        530.9                              Stage 2 Search

GlobalSearch stopped because it analyzed all the trial points.

3 out of 4 local solver runs converged with a positive local solver exit flag.

x = 1×2
10^-7 ×

    0.0414    0.1298

fval = 1.5467e-15

Il risolutore trova tre minimi locali, incluso il minimo globale vicino a [0,0].

Minimi locali multipli tramite `MultiStart`

Per cercare più minimi utilizzando MultiStart, per prima cosa bisogna creare una struttura del problema. Poiché il problema non è vincolato, utilizzare il risolutore fminunc. Imposta le opzioni per non visualizzare nulla sulla riga di comando.

problem = createOptimProblem('fminunc',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fminunc,'Display','off'));

Convalidare la struttura del problema eseguendola.

[x,fval] = fminunc(problem)

x = 1×2

    8.4420 -110.2602

fval = 435.2573

Crea un oggetto MultiStart predefinito.

ms = MultiStart;

Eseguire il risolutore per 50 iterazioni, registrando i minimi locali.

rng(1) % For reproducibility
[x,fval,eflag,output,manymins] = run(ms,problem,50)

MultiStart completed some of the runs from the start points. 

10 out of 50 local solver runs converged with a positive local solver exitflag.

x = 1×2

  -73.8348 -197.7810

fval = 766.8260

eflag = 2

output = struct with fields:
                funcCount: 8574
         localSolverTotal: 50
       localSolverSuccess: 10
    localSolverIncomplete: 40
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points. ...'

manymins=1×10 GlobalOptimSolution array with properties:
    X
    Fval
    Exitflag
    Output
    X0

Il risolutore non trova il minimo globale vicino a [0,0] . Il risolutore trova 10 minimi locali distinti.

Rappresentare graficamente i valori della funzione nei minimi locali:

histogram([manymins.Fval],10)

Rappresenta i valori della funzione nei tre punti migliori:

bestf = [manymins.Fval];
histogram(bestf(1:3),10)

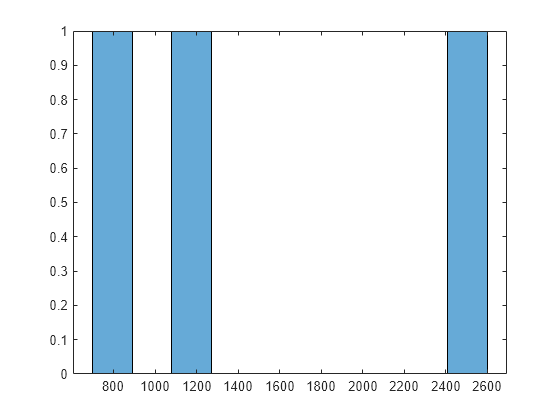
MultiStart avvia fminunc dai punti di partenza con componenti distribuite uniformemente tra –1000 e 1000. fminunc spesso rimane bloccato in uno dei tanti minimi locali. fminunc supera il limite di iterazione o il limite di valutazione della funzione 40 volte.

Vedi anche

GlobalSearch | MultiStart | createOptimProblem

Trova i minimi globali o multipli locali

Singolo minimo globale tramite GlobalSearch

Minimi locali multipli tramite MultiStart

Vedi anche

Argomenti

Singolo minimo globale tramite `GlobalSearch`

Minimi locali multipli tramite `MultiStart`