Fixed-Point Type Conversion and Refinement

Open Script

This example shows how to achieve your desired numerical accuracy when converting fixed-point MATLAB® code to floating-point code using the HDL Workflow Advisor.

Introduction

The floating-point to fixed-point conversion workflow in HDL Coder™ includes the following steps:

Verify the floating-point design is compatible for code generation.
Compute fixed-point types based on the simulation of the testbench.
Generate readable and traceable fixed-point MATLAB® code.
Verify the generated fixed-point design.

This tutorial uses Kalman filter suitable for HDL code generation to illustrate some key aspects of fixed-point conversion workflow, specifically steps 2 and 3 in the above list.

MATLAB Design

The MATLAB code used in this example implements a simple Kalman filter. This example also contains a MATLAB testbench that exercises the filter.

Kalman filter implementation suitable for HDL code generation

design_name = 'mlhdlc_kalman_hdl';
testbench_name = 'mlhdlc_kalman_hdl_tb';

edit('mlhdlc_kalman_hdl')
edit('mlhdlc_kalman_hdl_tb')

Simulate the Design

Simulate the design with the testbench prior to code generation to make sure there are no runtime errors.

mlhdlc_kalman_hdl_tb

Running --------> mlhdlc_kalman_hdl_tb

Current plot held
Current plot released

Create a New HDL Coder Project

To create a new project, enter the following command:

  coder -hdlcoder -new flt2fix_project

Next, add the file mlhdlc_kalman_hdl.m to the project as the MATLAB Function and mlhdlc_kalman_hdl_tb.m as the MATLAB Test Bench.

Refer to Get Started with MATLAB to HDL Workflow for a more complete tutorial on creating and populating MATLAB HDL Coder projects.

Fixed-Point Code Generation Workflow

Perform the following tasks before moving on to the fixed-point type proposal step:

Click the Workflow Advisor button to launch the HDL Workflow Advisor.
Choose Convert to fixed-point at build time for the Fixed-point conversion option.
Click Run button to define input types for the design from the testbench.
Select the Fixed-Point Conversion workflow step.
Click Analyze to execute the instrumented floating-point simulation.

Refer to Floating-Point to Fixed-Point Conversion for a more complete tutorial on these steps.

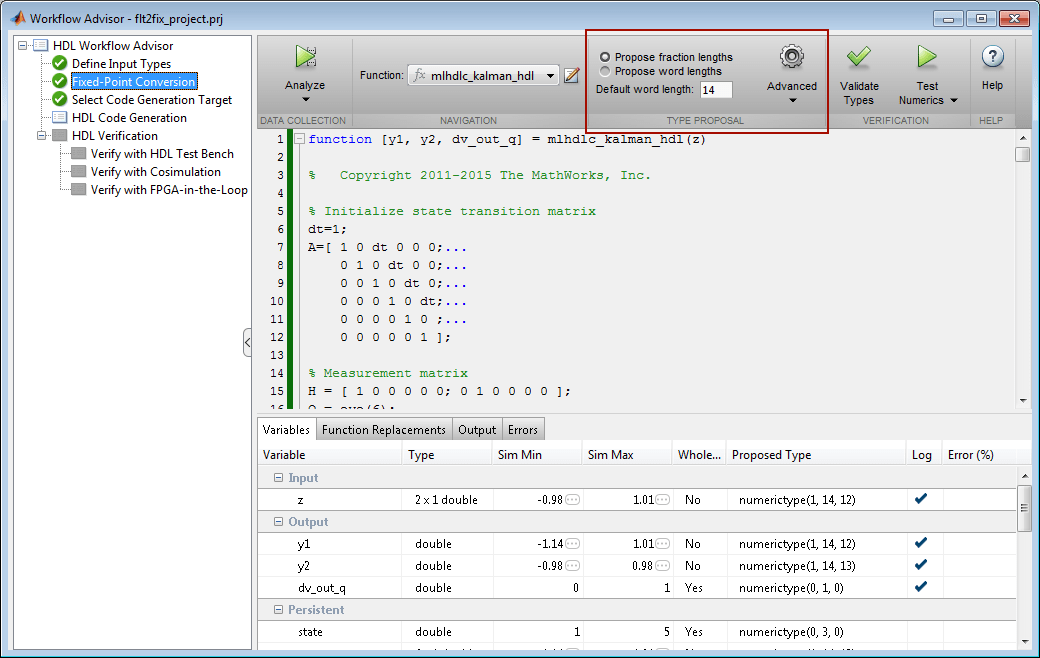
Determine the Initial Fixed Point Types

After instrumented floating-point simulation completes, Fixed-Point Types are proposed based on the simulation results.

At this stage of the conversion proposes fixed-point types for each variable in the design based on the recorded min/max values of the floating point variables and user input.

At this point, for all variables, you can (re)compute and propose:

Fraction lengths for a given fixed word length setting, or
Word lengths for a given fixed fraction length setting.

Choose the Word Length Setting

When you are starting with a floating-point design and going through the floating-point to fixed-point conversion for the first time, it is a good practice to start by specifying a 'Default Word Length' setting based on the largest dynamic range of all the variables in the design.

In this example, we start with a default word length of 22 and run the 'Propose Fixed-Point Types' step.

Explore the Proposed Fixed-Point Type Table

The type table contains the following information for each variable, organized by function, existing in the floating-point MATLAB design:

Sim Min: The minimum value assigned to the variable during simulation.
Sim Max: The maximum value assigned to the variable during simulation.
Whole Number: Whether all values assigned during simulation are integer.

The type proposal step uses the above information and combines it with the user-specified word length settings to propose a fixed-point type for each variable.

You can also use Compute Derived Range Analysis to compute derived ranges and that is covered in detail in this tutorial Fixed-Point Type Conversion and Derived Ranges.

Interpret the Proposed Numeric Types for Variables

Based on the simulation range (min & max) values and the default word length setting, a numeric type is proposed for each variable.

The following table shows numeric type proposals for a Default word length of 22 bits.

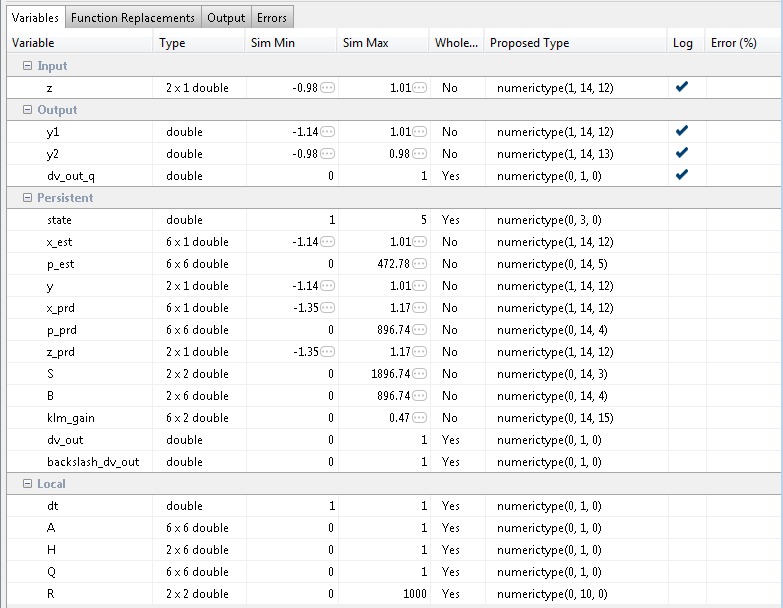
Examine the types proposed in the above table for variables instrumented in the top-level design.

Floating-Point Range for variable B:

Simulation Info: SimMin: 0, SimMax: 896.74.., Whole Number: No
Type Proposed: numerictype(0,22,12) (Signedness: Unsigned, WordLength: 22, FractionLength: 12)

The floating-point range:

Has the same number of bits as the Default word length.
Uses the minimum number of bits to completely represent the range.
Uses the rest of the bits to represent the precision.

Integer Range for variable A:

Simulation Info: SimMin: 0, SimMax: 1, Whole Number: Yes
Type Proposed: numerictype(0,1,0) (Signedness: Unsigned, WordLength: 1, FractionLength: 0)

The integer range:

Has the minimum number of bits to represent the whole integer range.
Has no fractional bits.

All the information in the table is editable, persists across iterations, and is saved with your code generation project.

Generate Fixed-Point Code and Verify the Generated Code

Based on the numeric types proposed for a default word length of 22, continue with fixed-point code generation and verification steps and observe the plots.

Click on Validate Types to apply computed fixed-point types.
Next choose the option Log inputs and outputs for comparison plots and then click on the Test Numerics to rerun the testbench on the fixed-point code.

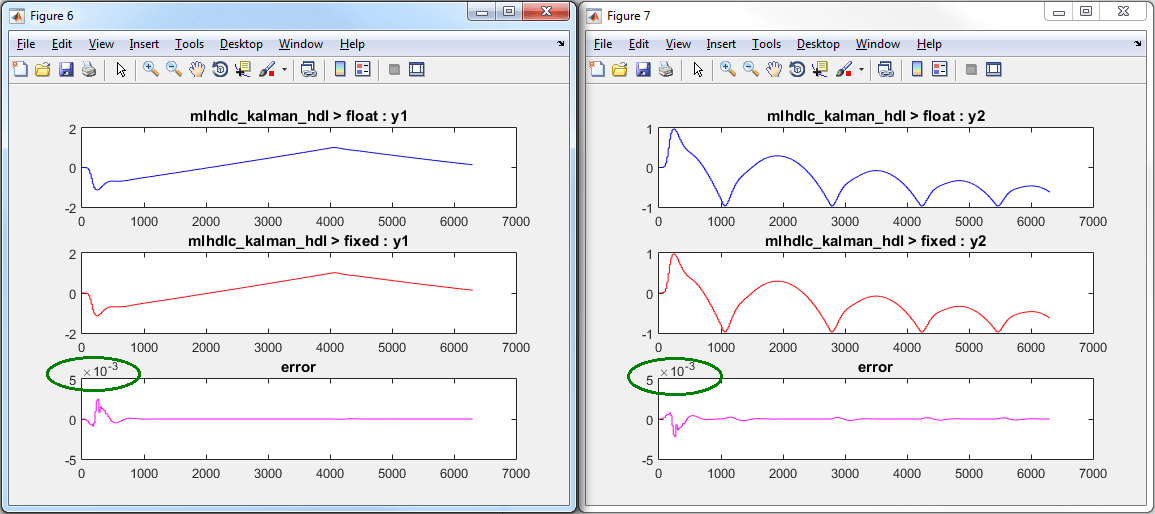
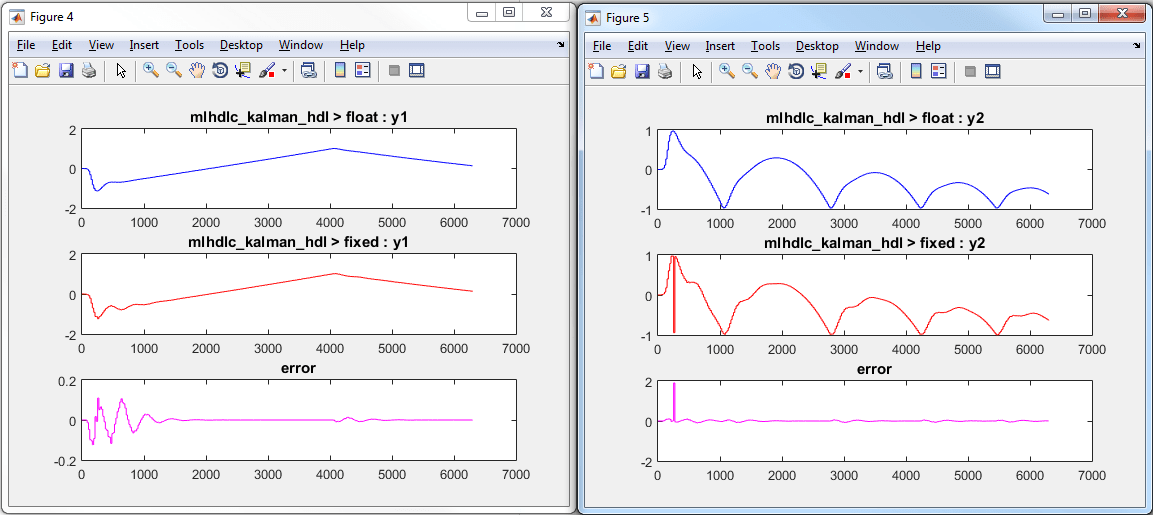
The plot on the left is generated from testbench during the simulation of floating-point code, the one on the right is generated from the simulation of the generated fixed-point code. Notice, the plots do not match.

Having chosen comparison plots option you will see additional plots that compare the floating and fixed point simulation results for each output variable.

Examine the error graph for each output variable. It is very high for this particular design.

Iterate on the Results

One way to reduce the error is to increase Default word length and repeat the fixed-point conversion.

In this example design, when a word length of 22 bits is chosen there is a lot of truncation error when representing the precision. More bits are required to the right of the binary point to reduce the truncation errors.

Let us now increase the default word length to 28 bits and repeat the type proposal and validation steps.

Select a Default word length of 28.

Changing default word length automatically triggers the type proposal step and new fixed-point types are proposed based on the new word length setting. Also notice that type validation needs to be rerun and numerics need to be verified again.

Click on Validate Types.
Click on Test Numerics to rerun the testbench on the fixed-point code.

Once these steps are complete, re-examine the comparison plots and notice that the error is now roughly three orders of magnitude smaller.