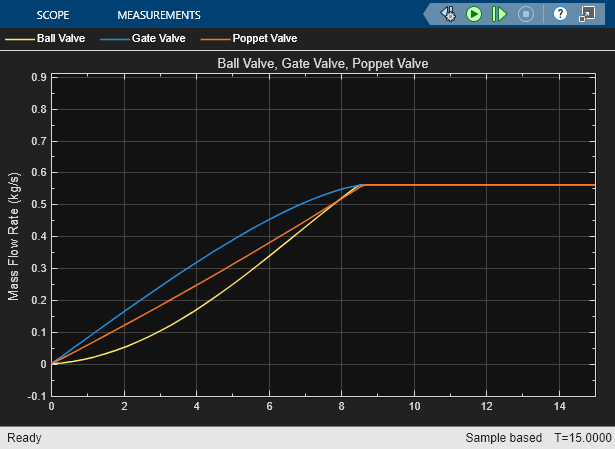
Ball Valve (IL)
Libraries:
Simscape /
Fluids /
Isothermal Liquid /
Valves & Orifices /
Flow Control Valves
Description
The Ball Valve (IL) block represents a ball valve in an isothermal liquid network. A ball valve consists of a ball with a bore that can pivot inside of a valve body. When the valve is open, the bore fully overlaps with the valve body port. As the valve shuts, the ball rotates and reduces the amount of overlap, thereby reducing the effective area of the orifice. Ball valves are common for flow isolation purposes because they can securely shut off flow for many cycles. Ball valves are less common in applications where precise throttling is necessary.
You can parameterize the block analytically or by using tabulated data. When you set
Opening characteristic to Area of overlapping
circles, the block considers the area of the overlap between the valve
port and the ball bore as the opening area such that
where:
Rport and Rbore are the radii of the valve port and the ball bore, respectively.
l is the displacement of the bore center from the valve port center.
φ is the rotation of the ball valve given by the physical signal S. The valve is fully shut at 0 rad and fully open at π/2 rad.
Mass Flow Rate
The block calculates flow through the valve using the pressure-area relationship for orifices such that
where:
Cd is the discharge coefficient.
is the average fluid density.
A is the area open to flow, where A = Aopen + Aleak, and Aleak is the Leakage area parameter.
Δpcrit is the critical pressure differential associated with the critical Reynolds number, Recrit.
The block calculates Δpcrit as
When you set Valve parameterization to
Orifice area based on geometry, you can specify
Cd using the Discharge
coefficient parameter. When you set Valve
parameterization to Cv flow coefficient,
the block calculates Cd as
where Cv is the
Maximum Cv flow coefficient parameter. When you set
Valve parameterization to Kv flow
coefficient, the block uses
where Kv is the Maximum Kv flow coefficient parameter. In either equation, ΔpCv is 1 psi and ΔpKv is 1 bar.