Counterbalance Valve with Boom Arm
This example shows how to model, parameterize, test, and compare design cases for a counterbalance valve in a boom arm mechanism. A counterbalance valve allows an upstream flow from the back port to the load port through the check valve stage during cylinder rod extension, and it allows a downstream flow from the load port to the back port through the relief valve stage during cylinder rod retraction in the boom arm mechanism. Counterbalance valves help with the load holding, load actuation, speed control, and safety by controlling the piston motion of the booming cylinder. When you run the model, it generates a plot of the booming cylinder position and the forces at the A side and B side of the cylinder piston.
Model
The following figure shows the model of a counterbalance valve with a boom arm.

Crane Boom Arm with Booming Cylinder Subsystem: Connection Booming A and Booming B are the isothermal liquid ports associated with the cap and rod side hydraulic nodes of the booming cylinder.

Boom Arm and Booming Cylinder Kinematics Subsystem: This subsystem demonstrates how to compute the link angles relative to one another and the force applied by the boom arm on the booming cylinder rod.


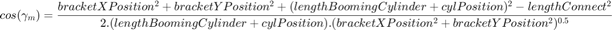
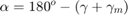


where,
 is the bracket
is the bracket is the booming cylinder
is the booming cylinder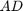 is the boom arm
is the boom arm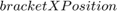 is the booming cylinder connection location to the bracket (OB)
is the booming cylinder connection location to the bracket (OB) is the boom arm connection location to the bracket (OA)
is the boom arm connection location to the bracket (OA)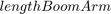 is the boom arm length
is the boom arm length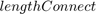 is the distance between the bracket and the connection point of the boom arm and the booming cylinder (AC)
is the distance between the bracket and the connection point of the boom arm and the booming cylinder (AC) is the booming cylinder rod extension length
is the booming cylinder rod extension length is the booming cylinder length
is the booming cylinder length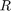 is the force applied to the booming cylinder by the boom arm
is the force applied to the booming cylinder by the boom arm

Simulation Results from Scope
This figure shows the booming cylinder position and the forces at the A side and B side of the cylinder piston.

Simulation Results from Simscape Logging
This figure shows the booming cylinder position and the pressures at the A side and B side of the cylinder piston.

This figure shows the booming cylinder position, directional control valve position, and the flow rates through the counterbalance valve for the design cases 1 and 2 of the counterbalance valve. The booming cylinder extends in the negative position of the direction control valve and retracts in the positive position of the direction control valve.


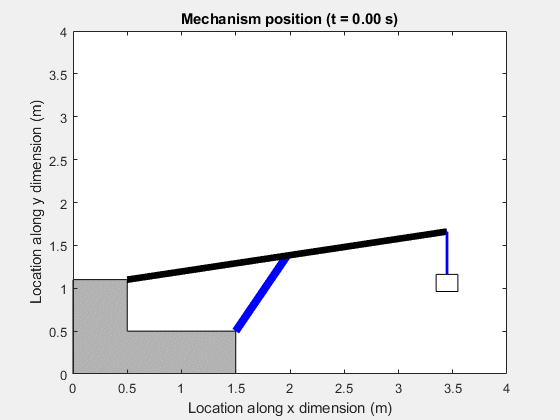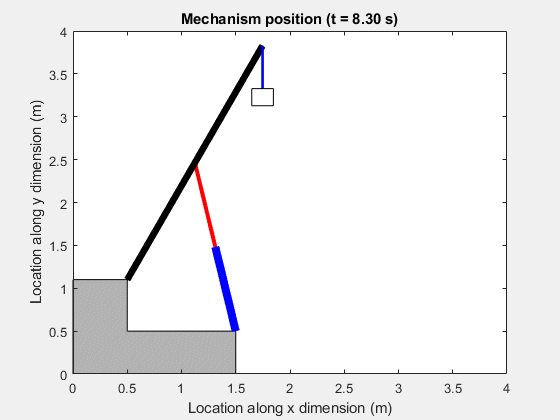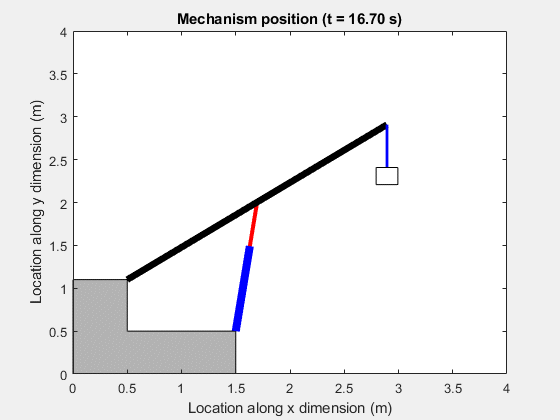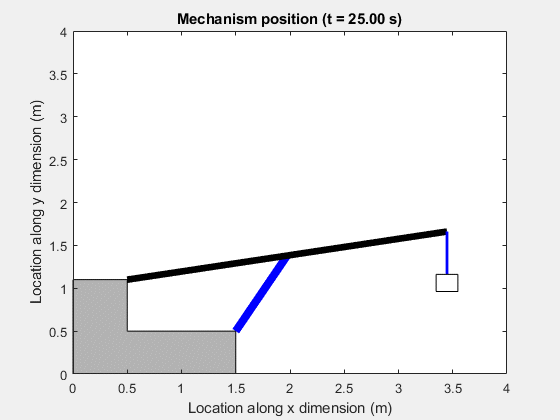
Animation of Simscape Logging Results
This animation shows the change in the position of the booming cylinder and boom arm mechanism. The motion in the mechanism is based on the flows to the cap side and rod side of the piston chamber of the booming cylinder through the counterbalance valve.