Poisson's Equation with Point Source and Adaptive Mesh Refinement
This example shows how to solve a Poisson's equation with a delta-function point source on the unit disk using the adaptmesh function.
Specifically, solve the Poisson's equation
on the unit disk with zero Dirichlet boundary conditions. The exact solution expressed in polar coordinates is
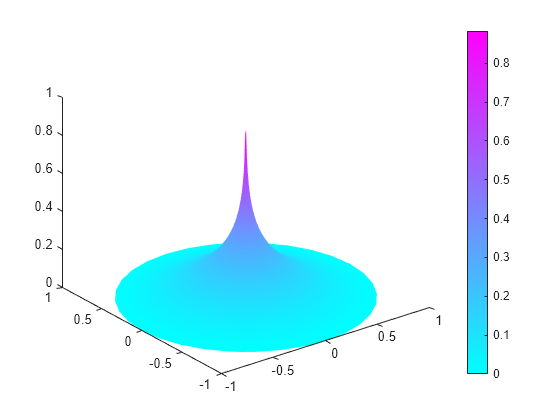
which is singular at the origin.
By using adaptive mesh refinement, Partial Equation Toolbox™ can accurately find the solution everywhere away from the origin.
The following variables define the problem:
c,a: The coefficients of the PDE.f: A function that captures a point source at the origin. It returns 1/area for the triangle containing the origin and 0 for other triangles.
c = 1; a = 0; f = @circlef;
Create a PDE Model with a single dependent variable.
numberOfPDE = 1; model = createpde(numberOfPDE);
Create a geometry and include it in the model.
g = @circleg; geometryFromEdges(model,g);
Plot the geometry and display the edge labels.
figure; pdegplot(model,"EdgeLabels","on"); axis equal title("Geometry With Edge Labels Displayed")
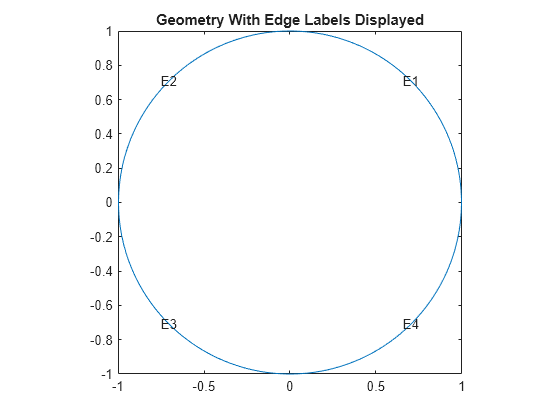
Specify the zero solution at all four outer edges of the circle.
applyBoundaryCondition(model,"dirichlet","Edge",(1:4),"u",0);
adaptmesh solves elliptic PDEs using the adaptive mesh generation. The tripick parameter lets you specify a function that returns which triangles will be refined in the next iteration. circlepick returns triangles with computed error estimates greater a given tolerance. The tolerance is provided to circlepick using the "par" parameter.
[u,p,e,t] = adaptmesh(g,model,c,a,f,"tripick", ... "circlepick", ... "maxt",2000, ... "par",1e-3);
Number of triangles: 258 Number of triangles: 515 Number of triangles: 747 Number of triangles: 1003 Number of triangles: 1243 Number of triangles: 1481 Number of triangles: 1705 Number of triangles: 1943 Number of triangles: 2155 Maximum number of triangles obtained.
Plot the finest mesh.
figure;
pdemesh(p,e,t);
axis equal
Plot the error values.
x = p(1,:)'; y = p(2,:)'; r = sqrt(x.^2+y.^2); uu = -log(r)/2/pi; figure; pdeplot(p,e,t,"XYData",u-uu,"ZData",u-uu,"Mesh","off");

Plot the FEM solution on the finest mesh.
figure; pdeplot(p,e,t,"XYData",u,"ZData",u,"Mesh","off");