Beta

Create Beta model object for exposure at default

Since R2022b

Description

Create and analyze a Beta model object to calculate the exposure at default (EAD) using this workflow:

1. Use fitEADModel to create a Beta model object.

2. Use predict to predict the EAD.

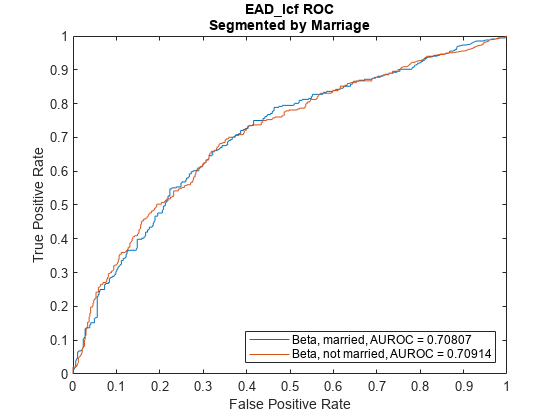
3. Use modelDiscrimination to return AUROC and ROC data. You can plot the results using modelDiscriminationPlot.

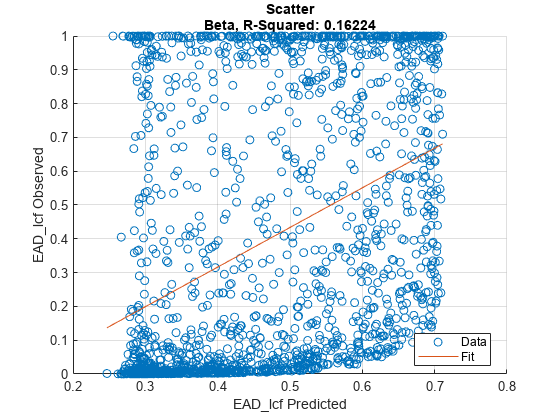
4. Use modelCalibration to return the R-squared, RMSE, correlation, and sample mean error of predicted and observed EAD data. You can plot the results using modelCalibrationPlot.

Creation

Syntax

BetaEADModel = fitEADModel(data,ModelType)

BetaEADModel = fitEADModel(___,Name=Value)

Description

BetaEADModel = fitEADModel(data,ModelType) creates a Beta EAD model object.

BetaEADModel = fitEADModel(___,Name=Value) specifies options using one or more name-value arguments in addition to the input arguments in the previous syntax. The optional name-value arguments set the model object properties. For example, BetaEADModel = fitEADModel(EADData,ModelType,PredictorVars={'UtilizationRate','Age','Marriage'},ConversionMeasure="lcf",DrawnVar='Drawn',LimitVar='Limit',ResponseVar='EAD') creates an BetaEADModel object using a Beta model type.

Input Arguments

data — Data for exposure at default

table

Data for exposure at default, specified as a table.

Data Types: table

ModelType — Model type

string with value "Beta" | character vector with value 'Beta'

Model type, specified as a string with the value of "Beta" or a character vector with the value of 'Beta'.

Data Types: char | string

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: BetaEADModel = fitEADModel(EADData,ModelType,PredictorVars={'UtilizationRate','Age','Marriage'},ConversionMeasure="lcf",LimitVar='Limit',ResponseVar='EAD',BoundaryTolerance=1e5)

ModelID — User-defined model ID

"Beta" (default) | string | character vector

User-defined model ID, specified as ModelID and a string or character vector. The software uses the ModelID text to format outputs and is expected to be short.

Data Types: string | char

Description — User-defined description for model

"" (default) | string | character vector

User-defined description for model, specified as Description and a string or character vector.

Data Types: string | char

PredictorVars — Predictor variables

all columns of data except for ResponseVar (default) | string array | cell array of character vectors

Predictor variables, specified as PredictorVars and a string array or cell array of character vectors. PredictorVars indicates which columns in the data input contain the predictor information. By default, PredictorVars is set to all the columns in the data input except for ResponseVar.

Data Types: string | cell

ResponseVar — Response variable

last column of data (default) | string | character vector

Response variable, specified as ResponseVar and a string or character vector. The response variable contains the EAD data and must be a numeric variable. By default, ResponseVar is set to the last column.

Data Types: string | char

BoundaryTolerance — Value to perturb EAD responses

1e-7 (default) | positive numeric

Value to perturb EAD response values away from 0 to 1, specified as BoundaryTolerance and a positive scalar numeric.

Data Types: double

LimitVar — Limit variable

string | character vector

Limit variable, specified as LimitVar and a string or character vector. LimitVar indicates which column in data contains the limit amount. The limit amount value in the data must be a positive numeric value. The limit depends on the loan. If the loan is a credit card, the limit is the credit limit. If the loan is a mortgage, the limit is the initial loan amount. In general, LimitVar is the maximum amount that can be borrowed.

Note

LimitVar is required when ConversionMeasure is 'lcf'. For more information on LCF, see Conversion Measure Options.

Data Types: string | char

DrawnVar — Drawn variable

string | character vector

Drawn variable, specified as DrawnVar and a string or character vector. DrawnVar is the balance on the account at the time of observation, before default, and EAD is the balance at the time of default. DrawnVar indicates which column in data contains the drawn amount. The drawn variable value in the data can be a positive or negative numeric value.

Note

When the ConversionMeasure is 'lcf', DrawnVar is not required. In this case, DrawnVar is set to "".

Data Types: string | char

ConversionMeasure — Conversion measure for EAD response values

"lcf" (default) | character vector with value 'lcf' | string with value "lcf"

Response transform, specified as ConversionMeasure and a character vector or string. Limit conversion factor (LCF) is a fraction of the limit representing the total exposure. The EAD is then defined as the LCF times the limit (EAD = LCF*Limit).

For more information on LCF, see Conversion Measure Options.

Data Types: string | char

SolverOptions — optimoptions object

object

Options for fitting, specified as SolverOptions and an optimoptions object that is created using optimoptions from Optimization Toolbox™. The defaults for the optimoptions object are:

• "Display" — "none"

• "Algorithm" — "quasi-newton"

• "MaxFunctionEvaluations" — 500 ✕ Number of model coefficients

• "MaxIterations" — 1000

Note

When using optimoptions with a Beta model, specify the SolverName as fminunc.

The number of Beta model coefficients is determined at run time, depending on the number of predictors and the number of categories in the categorical predictors.

Data Types: object

Properties

ModelID — User-defined model ID

Beta (default) | string

User-defined model ID, returned as a string.

Data Types: string

Description — User-defined description

"" (default) | string

User-defined description, returned as a string.

Data Types: string

UnderlyingModel — Underlying statistical model

compact linear model

This property is read-only.

Underlying statistical model, returned as a compact linear model object. The compact version of the underlying regression model is an instance of the risk.internal.credit.BetaModel class.

Data Types: object

PredictorVars — Predictor variables

all columns of data except for the ResponseVar (default) | string array

Predictor variables, returned as a string array.

Data Types: string

ResponseVar — Response variable

last column of data (default) | string

Response variable, returned as a string.

Data Types: string

LimitVar — Limit variable

string

Limit variable, returned as a string.

Data Types: string

DrawnVar — Drawn variable

string

Drawn variable, returned as a string.

Data Types: string

ConversionMeasure — Conversion measure for EAD response values

"lcf" (default) | string with value "lcf"

Response transform, returned as a string.

Data Types: string

BoundaryTolerance — Value to perturb LGD responses

1e-7 (default) | positive numeric

Value to perturb LGD response values away from 0 to 1, returned as a positive scalar numeric.

Data Types: double

Object Functions

predict	Predict exposure at default
modelDiscrimination	Compute AUROC and ROC data
modelDiscriminationPlot	Plot ROC curve
modelCalibration	Compute R-square, RMSE, correlation, and sample mean error of predicted and observed EADs
modelCalibrationPlot	Scatter plot of predicted and observed EADs

Examples

Create Beta EAD Model

This example shows how to use fitEADModel to create a Beta model object for exposure at default (EAD).

Load EAD Data

Load the EAD data.

load EADData.mat
head(EADData)

    UtilizationRate    Age     Marriage        Limit         Drawn          EAD    
    _______________    ___    ___________    __________    __________    __________

        0.24359        25     not married         44776         10907         44740
        0.96946        44     not married    2.1405e+05    2.0751e+05         40678
              0        40     married        1.6581e+05             0    1.6567e+05
        0.53242        38     not married    1.7375e+05         92506        1593.5
         0.2583        30     not married         26258        6782.5        54.175
        0.17039        54     married        1.7357e+05         29575        576.69
        0.18586        27     not married         19590          3641        998.49
        0.85372        42     not married    2.0712e+05    1.7682e+05    1.6454e+05

rng('default');
NumObs = height(EADData);
c = cvpartition(NumObs,'HoldOut',0.4);
TrainingInd = training(c);
TestInd = test(c);

Select Model Type

Select a model type for Beta.

ModelType = "Beta";

Select Conversion Measure

Select a conversion measure for the EAD response values.

ConversionMeasure = "LCF";

Create Beta EAD Model

Use fitEADModel to create a Beta model object using the TrainingInd data.

BetaEADModel = fitEADModel(EADData(TrainingInd,:),ModelType,PredictorVars={'UtilizationRate','Age','Marriage'}, ...
    ConversionMeasure=ConversionMeasure,LimitVar="Limit",ResponseVar="EAD",BoundaryTolerance=2e-05);
disp(BetaEADModel);

  Beta with properties:

    BoundaryTolerance: 2.0000e-05
              ModelID: "Beta"
          Description: ""
      UnderlyingModel: [1x1 risk.internal.credit.BetaModel]
        PredictorVars: ["UtilizationRate"    "Age"    "Marriage"]
          ResponseVar: "EAD"
             LimitVar: "Limit"
             DrawnVar: ""
    ConversionMeasure: "lcf"

Display the underlying model. The underlying model's response variable is the transformation of the EAD response data. Use the 'LimitVar' and 'DrawnVar' name-value arguments to modify the transformation.

disp(BetaEADModel.UnderlyingModel);

Beta regression model:
     logit(EAD_lcf) ~ 1_mu + UtilizationRate_mu + Age_mu + Marriage_mu
     log(EAD_lcf) ~ 1_phi + UtilizationRate_phi + Age_phi + Marriage_phi

Estimated coefficients:
                                 Estimate        SE         tStat        pValue  
                                __________    _________    ________    __________

    (Intercept)_mu                -0.68477       0.1145     -5.9807    2.5236e-09
    UtilizationRate_mu              1.7029     0.077717      21.912             0
    Age_mu                       -0.005633    0.0027489     -2.0492      0.040541
    Marriage_not married_mu      -0.025615     0.051927    -0.49328       0.62185
    (Intercept)_phi               -0.46429     0.095342     -4.8697    1.1838e-06
    UtilizationRate_phi            0.41621      0.06701      6.2112    6.0949e-10
    Age_phi                      -0.001282    0.0023261    -0.55114       0.58159
    Marriage_not married_phi    0.00014864     0.042884    0.003466       0.99723

Number of observations: 2627
Log-likelihood: -2931.19

Predict EAD

EAD prediction operates on the underlying compact statistical model and then transforms the predicted values back to the EAD scale. You can specify the predict function with different options for the 'ModelLevel' name-vale argument.

predictedEAD = predict(BetaEADModel,EADData(TestInd,:))

predictedEAD = 1751×1
105 ×

    0.1758
    0.1029
    0.1528
    0.0832
    0.3261
    0.5148
    0.0648
    0.0531
    0.0712
    0.3215
      ⋮

Validate EAD Model

For model validation, use modelDiscrimination, modelDiscriminationPlot, modelCalibration, and modelCalibrationPlot.

Use modelDiscrimination and then modelDiscriminationPlot to plot the ROC curve.

ModelLevel = "ConversionMeasure";

[DiscMeasure1,DiscData1] = modelDiscrimination(BetaEADModel,EADData(TestInd,:),ModelLevel=ModelLevel);
modelDiscriminationPlot(BetaEADModel,EADData(TestInd, :),ModelLevel=ModelLevel,SegmentBy="Marriage");

Use modelCalibration and then modelCalibrationPlot to show a scatter plot of the predictions.

YData = "Observed";

[CalMeasure1,CalData1] = modelCalibration(BetaEADModel,EADData(TestInd,:),ModelLevel=ModelLevel);
modelCalibrationPlot(BetaEADModel,EADData(TestInd,:),ModelLevel=ModelLevel,YData=YData);

Plot a histogram of observed EAD with respect to the predicted EAD.

figure;
histogram(CalData1.Observed);
hold on;
histogram(CalData1.(('Predicted_' + ModelType)));
legend('Observed','Predicted');

More About

Beta Regression Models

Beta regression models model continuous variables that assume values in the open standard unit interval (0, 1).

The beta regression model is based on the assumption that the dependent variable is beta-distributed and that its mean is related to a set of regressors through a linear predictor with unknown coefficients and a link function. The beta regression model also includes a precision parameter that may be constant or depend on a potentially different set of regressors through a link function as well.

If the variable takes on values in (a, b) with a < b, you can model (y - a) / (b - a). Also, if y also assumes the extremes 0 and 1, a useful transformation in practice is y (n - 1) + 0.5) / n, where n is the sample size.

The beta regression model is based on an alternative parameterization of the beta density in terms of the mean and a precision parameter: μ = a / (a + b) and φ = a + b, 0 < μ < 1, φ > 0.

$$\begin{array}{l}f(y;\mu ,\varphi )=\frac{\Gamma (\varphi )}{\Gamma (\mu \varphi )\Gamma ((1-\mu )\varphi )}{y}^{\mu \varphi -1}{(}^1,\text{ 0<}y\text{<1,}\\ y\text{~B(}\mu \text{,}\phi \text{) with E(}y\text{)=}\mu ,\text{ VAR(}\phi \text{)=}\mu \text{(1-}\mu \text{)/(1+}\phi \text{)}\end{array}$$

The beta regression model is defined as

$$\begin{array}{l}{g}_1({\mu }_i)={\eta }_{1i}=x_i^T\beta ,\\ g_2({\varphi }_i)={\eta }_{2i}=z_i^T\gamma ,\end{array}$$

where β = (β₀,β₁,…,β_k)^T, ᵞ = (ᵞ₀,ᵞ₁,…,ᵞ_k)^T are the regression coefficients, η_1i, η_2i are the linear predictors, and x_i, z_i are the independent variables. g₁ and g₂ are the link functions where g₁ is logit and g₂ is log.

Parameter estimation is performed by maximum likelihood (ML).

References

[1] Baesens, Bart, Daniel Roesch, and Harald Scheule. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Wiley, 2016.

[2] Bellini, Tiziano. IFRS 9 and CECL Credit Risk Modelling and Validation: A Practical Guide with Examples Worked in R and SAS. San Diego, CA: Elsevier, 2019.

[3] Brown, Iain. Developing Credit Risk Models Using SAS Enterprise Miner and SAS/STAT: Theory and Applications. SAS Institute, 2014.

[4] Roesch, Daniel and Harald Scheule. Deep Credit Risk. Independently published, 2020.

Version History

Introduced in R2022b

R2023a: modelAccuracy object function is renamed to modelCalibration function

The modelAccuracy object function is renamed to modelCalibration function. The use of modelAccuracy is discouraged, use modelCalibration instead.

R2023a: modelAccuracyPlot object function is renamed to modelCalibrationPlot function

The modelAccuracyPlot object function is renamed to modelCalibrationPlot function. The use of modelAccuracyPlot is discouraged, use modelCalibrationPlot instead.