Robust Tuning of Mass-Spring-Damper System
This example shows how to robustly tune a PID controller for an uncertain mass-spring-damper system modeled in Simulink®.
Simulink Model of Mass-Spring-Damper System
The mass-spring-damper depicted in Figure 1 is modeled by the second-order differential equation

where  is the force applied to the mass and
is the force applied to the mass and  is the horizontal position of the mass.
is the horizontal position of the mass.

Figure 1: Mass-Spring-Damper System.
This system is modeled in Simulink as follows:
open_system('rct_mass_spring_damper')

We can use a PID controller to generate the effort  needed to change the position
needed to change the position  . Tuning this PID controller is easy when the physical parameters
. Tuning this PID controller is easy when the physical parameters 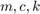 are known exactly. However this is rarely the case in practice, due to a number of factors including imprecise measurements, manufacturing tolerances, changes in operating conditions, and wear and tear. This example shows how to take such uncertainty into account during tuning to maintain high performance within the range of expected values for
are known exactly. However this is rarely the case in practice, due to a number of factors including imprecise measurements, manufacturing tolerances, changes in operating conditions, and wear and tear. This example shows how to take such uncertainty into account during tuning to maintain high performance within the range of expected values for 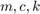 .
.
Uncertainty Modeling
The Simulink model uses the "most probable" or "nominal" values of 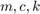 :
:

Use the "uncertain real" (ureal) object to model the range of values that each parameter may take. Here the uncertainty is specified as a percentage deviation from the nominal value.
um = ureal('m',3,'Percentage',40); uc = ureal('c',1,'Percentage',20); uk = ureal('k',2,'Percentage',30);
Nominal Tuning
First tune the PID controller for the nominal parameter values. Here we use two simple design requirements:
Position
 should track a step change with a 1 second response time
should track a step change with a 1 second response timeFilter coefficient
 in PID controller should not exceed 100.
in PID controller should not exceed 100.
These requirements are expressed as tuning goals:
Req1 = TuningGoal.Tracking('r','x',1); Req2 = TuningGoal.ControllerPoles('Controller',0,0,100);
Create an slTuner interface for tuning the "Controller" block in the Simulink model, and use systune to tune the PID gains and best meet the two requirements.
ST0 = slTuner('rct_mass_spring_damper','Controller'); ST = systune(ST0,[Req1 Req2]);
Final: Soft = 1.02, Hard = -Inf, Iterations = 44
Use getIOTransfer to view the closed-loop step response.
Tnom = getIOTransfer(ST,'r','x'); step(Tnom)

The nominal response meets the response time requirement and looks good. But how robust is it to variations of 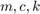 ?
?
Robustness Analysis
To answer this question, use the "block substitution" feature of slTuner to create an uncertain closed-loop model of the mass-spring-damper system. Block substitution lets you specify the linearization of a particular block in a Simulink model. Here we use this to replace the crisp values of 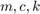 by the uncertain values
by the uncertain values um,uc,uk defined above.
blocksubs(1).Name = 'rct_mass_spring_damper/Mass'; blocksubs(1).Value = 1/um; blocksubs(2).Name = 'rct_mass_spring_damper/Damping'; blocksubs(2).Value = uc; blocksubs(3).Name = 'rct_mass_spring_damper/Spring Stiffness'; blocksubs(3).Value = uk; UST0 = slTuner('rct_mass_spring_damper','Controller',blocksubs);
To assess the robustness of the nominal tuning, apply the tuned PID gains to the (untuned) uncertain model UST0 and simulate the "uncertain" closed-loop response.
% Apply result of nominal tuning (ST) to uncertain closed-loop model UST0 setBlockValue(UST0,getBlockValue(ST)); Tnom = getIOTransfer(UST0,'r','x'); rng(0), step(Tnom,25), grid

The step plot shows the closed-loop response with the nominally tuned PID for 20 randomly selected values of 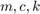 in the specified uncertainty range. Observe the significant performance degradation for some parameter combinations, with poorly damped oscillations and a long settling time.
in the specified uncertainty range. Observe the significant performance degradation for some parameter combinations, with poorly damped oscillations and a long settling time.
Robust Tuning
To improve the robustness of the PID controller, re-tune it using the uncertain closed-loop model UST0 rather than the nominal closed-loop model ST0. Due to the presence of ureal components in the model, systune automatically tries to maximize performance over the entire uncertainty range. This amounts to minimizing the worst-case value of the "soft" tuning goals Req1 and Req2.
UST0 = slTuner('rct_mass_spring_damper','Controller',blocksubs); UST = systune(UST0,[Req1 Req2]);
Soft: [1.02,4.9], Hard: [-Inf,-Inf], Iterations = 44 Soft: [1.03,1.41], Hard: [-Inf,-Inf], Iterations = 29 Soft: [1.04,1.04], Hard: [-Inf,-Inf], Iterations = 21 Final: Soft = 1.04, Hard = -Inf, Iterations = 94
The robust performance is only slightly worse than the nominal performance, but the same uncertain closed-loop simulation shows a significant improvement over the nominal design.
Trob = getIOTransfer(UST,'r','x'); rng(0), step(Tnom,Trob,25), grid legend('Nominal tuning','Robust tuning')

This is confirmed by plotting the worst-case gain from  to
to  as a function of frequency. Note the attenuated resonance near 1 rad/s.
as a function of frequency. Note the attenuated resonance near 1 rad/s.
clf
subplot(121), wcsigmaplot(Tnom,{1e-2,1e2}), grid
set(gca,'YLim',[-20 10]), title('Nominal tuning')
subplot(122), wcsigmaplot(Trob,{1e-2,1e2}), grid
set(gca,'YLim',[-20 10]), title('Robust tuning'), legend('off')
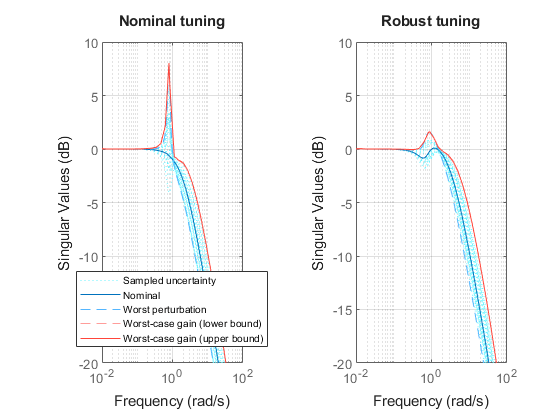
A comparison of the two PID controllers shows similar behaviors except for one key difference. The nominally tuned PID excessively relies on "cancelling" (notching out) the plant resonance, which is not a robust strategy in the presence of uncertainty on the resonance frequency.
Cnom = getBlockValue(ST,'Controller'); Crob = getBlockValue(UST,'Controller'); clf, bode(Cnom,Crob), grid legend('Nominal tuning','Robust tuning')

For further insight, plot the performance index (maximum value of the "soft" tuning goals Req1,Req2) as a function of the uncertain parameters  for the nominal damping
for the nominal damping  . Use the "varying parameter" feature of
. Use the "varying parameter" feature of slTuner to create an array of closed-loop models over a grid of  values covering their uncertainty ranges.
values covering their uncertainty ranges.
% Specify a 6-by-6 grid of (m,k) values for linearization ms = linspace(um.Range(1),um.Range(2),6); ks = linspace(uk.Range(1),uk.Range(2),6); [ms,ks] = ndgrid(ms,ks); params(1).Name = 'm'; params(1).Value = ms; params(2).Name = 'k'; params(2).Value = ks; STP = slTuner('rct_mass_spring_damper','Controller',params); % Evaluate performance index over (m,k) grid for nominally tuned PID setBlockValue(STP,'Controller',Cnom) [~,F1] = evalGoal(Req1,STP); [~,F2] = evalGoal(Req2,STP); Fnom = max(F1,F2); % Evaluate performance index over (m,k) grid for robust PID setBlockValue(STP,'Controller',Crob) [~,F1] = evalGoal(Req1,STP); [~,F2] = evalGoal(Req2,STP); Frob = max(F1,F2); % Compare the two performance surfaces clf subplot(211), surf(ms,ks,Fnom) xlabel('m'), ylabel('k'), zlabel('Performance'), title('Nominal tuning (c=1)') subplot(212), surf(ms,ks,Frob), set(gca,'ZLim',[1 2]) xlabel('m'), ylabel('k'), zlabel('Performance'), title('Robust tuning (c=1)')

This plot shows that the nominal tuning is very sensitive to changes in mass  or spring stiffness
or spring stiffness  , while the robust tuning is essentially insensitive to these parameters. To complete the design, use
, while the robust tuning is essentially insensitive to these parameters. To complete the design, use writeBlockValue to apply the robust PID gains to the Simulink model and proceed with further validation in Simulink.
writeBlockValue(UST)