Analyze Tradeoffs Between Performance and Fidelity

Designing physical system models involves balancing model performance and fidelity compared to a real system. Increasing the fidelity of your model yields more accurate results but also increases the computational requirements. Applications such as hardware-in-the-loop (HIL) simulation have strict computational cost requirements. For these applications, many blocks have parameterizations with the phrase Suitable for HIL Simulation. These parameterizations use abstractions to reduce computational cost and increase speed. You can also improve performance by omitting some physics or lumping parameters. When you adjust fidelity to improve performance, verify that the updated model results are acceptable compared to the baseline.

Lower fidelity models prioritize computational efficiency, which allows for faster simulation times and more seamless integration with hardware systems. High-fidelity models use more computational resources to capture physical detail with more accurate results. High-fidelity models may not be suitable for HIL because they require more resources than the target hardware has. For HIL, your specific computational cost requirements depend on your target hardware.

Simplify a Model for Better Performance

You can make a model run faster by avoiding elements that cause discontinuities or fast dynamics. Elements such as hard stops or backlash, stick-slip friction, and clutches are prone to discontinuities. Small masses connected to stiff springs without sufficient damping can cause fast system dynamics that increase the computation cost for a time step.

To see a model that you can configure for performance or high-fidelity, open the Vehicle with Four-Wheel Drive model. Enter:

openExample('sdl/VehicleWithFourWheelDriveExample')

This model uses the Generic Engine block, labeled Engine, to provide torque to the system. The Torque Converter block acts as a damper between the engine and the Simple Gear block labeled Gearbox. The Gearbox block transfers torque to both Differential blocks. The four tire blocks convert the rotational energy into translational energy to propel the Vehicle Body block, which calculates the interactions between the tires and the road surface.

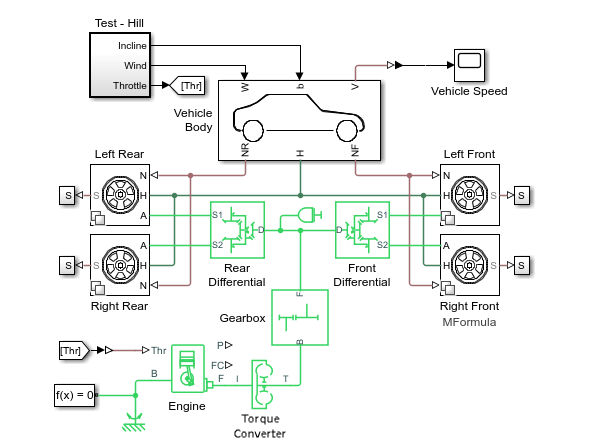
The four tire blocks are Variant Subsystem blocks that contain three tire variants. Each variant uses a different block to represent the tire dynamics. Double-click the Left Front subsystem to see the active and inactive variants. To learn more, see Variant Subsystem, Variant Model, Variant Assembly Subsystem.

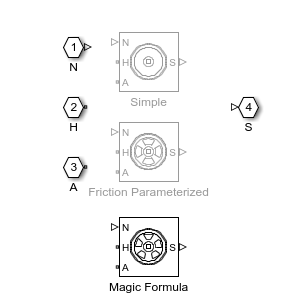
The inactive variants are light gray on the canvas. You can double-click any variant to see the implementations.

The default implementation uses the Tire (Magic Formula) block, which calculates the tire using slip angle, longitudinal slip, and vertical load. This block results in high-fidelity calculations, but the model runs slower to simulate than the other two implementations. The Simple subsystem uses the Tire (Simple) block, which represents a simple no-slip model. Using this subsystem results in a faster model and lower fidelity tire calculations.

Return to the top level of the model canvas. To enable the Simple variant on all four tires, click the Simple hyperlink in bullet 2 of the example links or enter:

VehicleWithFourWheelDriveSetTires(bdroot,'simple')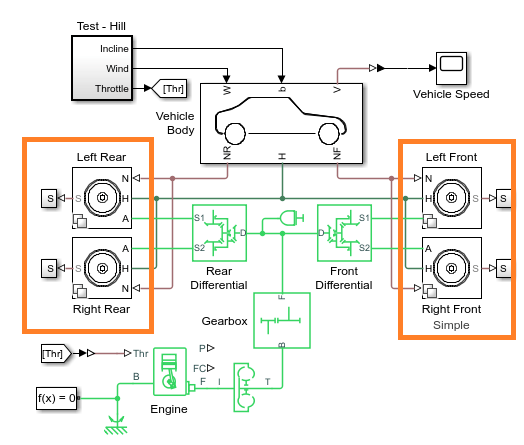

Now all four tires use the Simple parameterization. To confirm that the Gearbox, Front Differential, and Rear Differential blocks are configured for speed, check that Friction model is No meshing losses - Suitable for HIL Simulation. Also confirm that Enable backlash is cleared for the Simple Gear block. The model is now less complex and can run faster than the default model.

To run the faster model to collect data and plot the time step information, enter:

sim('VehicleWithFourWheelDrive')
simlogRef = simlog_VehicleWithFourWheelDrive;
tireRefNode = simlogRef.Left_Rear.Simple.Tire_Simple.A.w;
tRef = tireRefNode.series.time;
semilogy(tRef(1:end-1),diff(tRef),'-x')
title('Solver Step Size')
xlabel('Time (s)')
ylabel('Step Size (s)')
legend('Simple Tire',location='best')

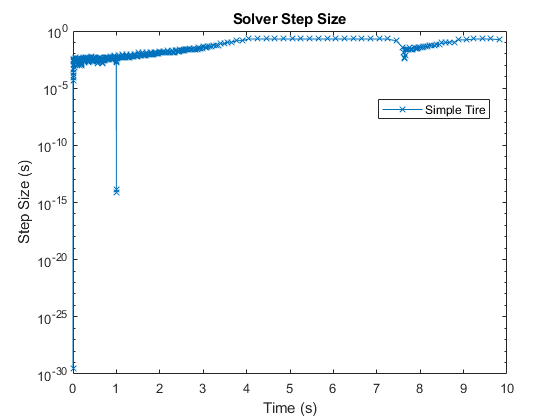
The spike that occurs one second into the simulation indicates that an event caused the solver to take a smaller time step.

Visualize the Difference Between Performance and Fidelity

Now that you have baseline results using a simple implementation of the model, you can analyze the performance cost or benefit of changing model fidelity. Switch the tire variants back to the Tire (Magic Formula) block, run the simulation, and plot the results.

VehicleWithFourWheelDriveSetTires(bdroot,'MFormula')
sim('VehicleWithFourWheelDrive')
simlogRef = simlog_VehicleWithFourWheelDrive;
tireRefNode = simlogRef.Left_Rear.Magic_Formula.Tire_Magic_Formula.A.w;
tRef = tireRefNode.series.time;
hold on
semilogy(tRef(1:end-1),diff(tRef),'-o')
legend('Simple Tire','Magic Formula Tire',location='best')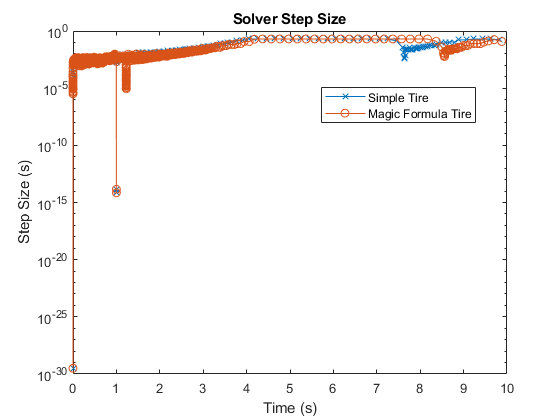

The Magic Formula parameterization is high-fidelity. The denser grouping of time steps at the beginning of the simulation indicates that the model takes longer to initialize. After the first spike at one second into the simulation, the solver reaches a second spike with a slow recovery. Compared to the simple tire parameterization, the solver takes extra resources to compute the results. The smaller step sizes are the result of capturing additional physical behavior in the simulation. The high-fidelity implementation captured an event at approximately 1.2 seconds that the simple tire implementation did not. Zoom in on the results to get a better view.

Also, at approximately eight seconds, the high-fidelity implementation shows an event that occurs later than in the simple implementation.

The high-fidelity model captures more detailed and more accurate results but takes longer to simulate and takes smaller solver steps. You can gain more detailed insights about the simulation by using the Solver Profiler. To learn more about solver step size and real-time model preparation, see Determine Step Size.